
Author: Youngjin Kang Date: September 22, 2024
This is Part 7 of the series, "Game Programming in Prolog". In order to understand what is going on in this article, please read Part 1 first.
There is one major feature which has been missing so far. It is the ability to create brand new actors while the game is running.
In all of the preceding examples, I declared the presence of actors by manually typing their names (i.e. IDs) and manually designating spawn-times and spawn-positions to them. If you have read my previous articles, you will definitely be able to tell that I had to explicitly write the following lines to spawn an actor called "actor1" at time 0 and position <0, 0>.
spawnTime(actor1, 0).
spawnPosition(actor1, <0, 0>).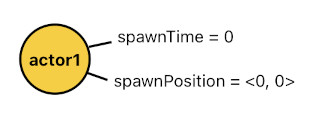
Here, the word "actor1" is something I just typed right inside the Prolog code - an arbitrary symbol which was not generated by the computer, but was entirely made up by the programmer. And in order to have multiple actors inside the game, I had to come up with a multitude of such made-up words and associate each one of them with its appropriate parameters. The code below is what I had to write in order to let the game have 3 actors in it, for instance.
spawnTime(actor1, 0).
spawnPosition(actor1, <0, 0>).
spawnTime(actor2, 0).
spawnPosition(actor2, <1, 0>).
spawnTime(actor3, 0).
spawnPosition(actor3, <2, 0>).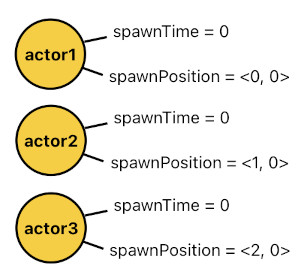
This is an okay approach, as long as there are only a handful of actors in total. If there are too many of them, however, it will be too cumbersome to write code for all of them individually. So, whenever that's the case, we usually find it helpful to contrive some kind of "code generator" which will automatically write a bunch of repetitive code for us. The following code snippet is a Javascript implementation of such a generator; it creates a chunk of Prolog code which spawns 100 actors (named "actor0", "actor1", "actor2", ... , "actor99") at random locations, right at the beginning of the game (n = 0).
function writeSpawningCode(actorId, time, posX, posY, prologCodeLines)
{
prologCodeLines.push(`spawnTime(${actorId}, ${time}).`);
prologCodeLines.push(`spawnPosition(${actorId}, <${posX}, ${posY}>).`);
}
function generatePrologCode()
{
const prologCodeLines = [];
for (let i = 0; i < 100; ++i)
{
const posX = Math.floor(Math.random() * 10);
const posY = Math.floor(Math.random() * 10);
writeSpawningCode(`actor${i}`, 0, posX, posY, prologCodeLines);
}
return prologCodeLines.join("\n");
}Even this fairly cunning technique, however, does not solve the very essence of the problem.
The fact that we are able to conveniently allocate a huge number of actors is indeed a good news, and it does open up a plethora of opportunities in regard to the richness of gameplay. However, we still have not figured out how to spontaneously create new actors out of nowhere while the game is running, instead of pre-defining them beforehand.
The ability to dynamically spawn new actors is crucial for implementing the concept of life and death in our gameplay system. As time passes by, old things die and new things are born. And every time a new thing comes into existence, it must be given its own identifier (ID) to let the system distinguish it from other things. The key is to come up with a unique identifier every time the game decides to create something new.
What is so tricky is that it is quite difficult to come up with an identifier which is truly unique, as opposed to one which may coincide with those which have already been hanging out elsewhere.
Certain types of constraints may let us easily bypass this issue, of course. If we only allow the game world to spawn up to 1 actor per time step, for example, we will be able to tell that simply using the current time step (i.e. value of 'n') as the new actor's ID will neatly solve the problem of uniqueness.
Obviously, we do not want such a harsh technical limitation in our game. Multiple actors should be able to be born at each time step, without having to wait in some kind of "spawn queue" before entering the world. Such a forced delay will be so awkward in cases in which we are required to instantiate things immediately (e.g. shooting bullets).
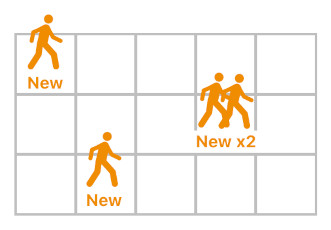
Another potential solution is to assume that only up to 1 actor will be born at each position in space, at each time step. As long as this supposition holds, each tuple formed by the actor's spawn-time and spawn-position (i.e. "n_x_y") will be guaranteed to be unique. This too, however, is a bit too restrictive since it disallows us from spawning multiple actors at the same spot simultaneously (which may sometimes be necessary, such as when spawning a mother kangarooo with a baby kangaroo in its pouch).
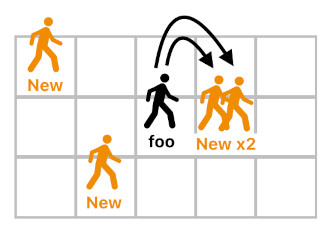
We may as well consider building the actor's ID by concatenating not just its spawn-time and spawn-position, but also the ID of the source of its birth (i.e. the actor from which it originated). So, if an actor called "foo" gave birth to a new actor at time 'n' and position <x,y>, the ID of the new actor could be expressed as "foo_n_x_y".
This, however, does not handle all the plausible edge cases either. What if "foo" decides to give birth to two different actors at the same exact spot at once? When that happens, the IDs of the two offsprings will be identical.
One may wonder why I am so morbidly concerned with such details, while we could just create a global integer variable (e.g. "int lastUsedId = 0"), increment it by 1 and use it as the new ID each time we spawn something. This is perhaps the most straightforward way of doing it in an imperative and single-threaded programming environment, where events are happening sequentially.
Note, however, that multiple events may occur concurrently in our Prolog environment if they belong to the same time step. Enforcing a specific order of operation among them will unjustly limit the power of declarative programming, and invalidate the reason why one would even bother to code in Prolog in the first place. One of the main reasons why logic programming is so great is that its procedures are order-independent (which prevents all sorts of race conditions and enables a significant portion of the code to run in parallel); we've really got to preserve this aspect of the language we are using.
Fortunately, there is a trick we can use to solve the problem of ID generation quite nicely. In order to demonstrate how this trick works, I will first come up with a scenario which involves a chicken and its eggs.
Imagine that there is a chicken which lays an egg each time the clock ticks (i.e. time step increments by 1). Suppose, for now, that it is only capable of laying up to 1 egg at a time (That is, no two or more eggs can be laid simultaneously). The predicate which denotes the act of laying an egg is shown below, where "n" is the time at which the egg was born and X is the ID of the chicken which laid it.
chicken[n](X) :- chicken[n-1](X).
layEgg[n](X) :- chicken[n](X).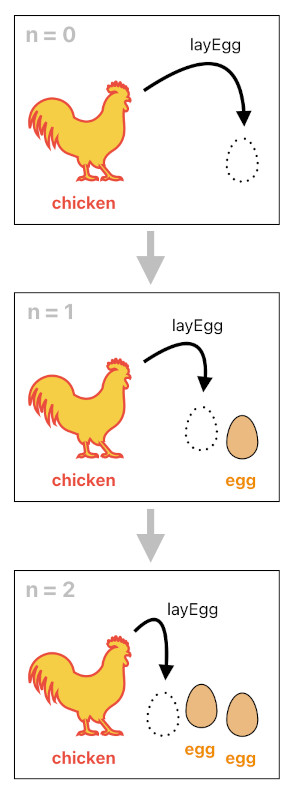
This means that, as long as we know that an egg happened to spawn at time "k" due to the act of "laying an egg" which was committed by a chicken called "foo", we are able to assure that this is the only egg which could have possibly been produced by "foo" at time "k". Why? Because "foo" and "k" are the only differentiating factors during the process of instantiation of the "layEgg[k](foo)" predicate.
The event "layEgg" is unique to a particular combination between the egg's source (X) and the time at which it was born (n). At each moment in time, therefore, there can only be at most one instance of "layEgg" which could originate from a particular chicken. The implication of this is that the expression "n_Src_layEgg", in which "n" is the time at which the event "layEgg" took place and "Src" is the ID of the chicken which laid the egg, must be unique for every single egg. Do you know what this means? It means that "n_Src_layEgg" can be used as the egg's unique ID.
The following code shows how this logic works.
layEgg[n](X) :- chicken[n](X).
spawn[n](X, layEgg, Pos) :- layEgg[n](X), position[n](X, Pos).
spawned[n]("{n}_{Src}_{Cause}", Src, Cause, Pos) :- spawn[n-1](Src, Cause, Pos).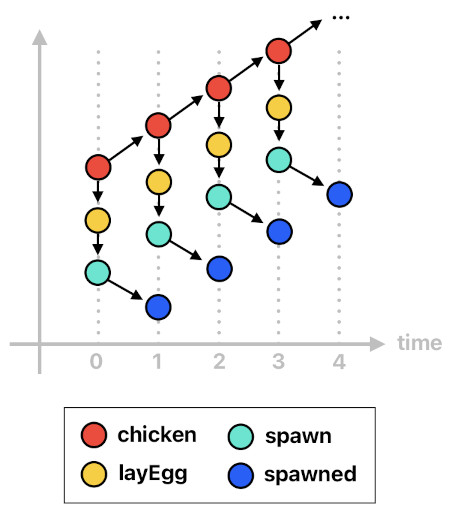
The first horn clause simply states that a chicken is supposed to lay an egg at each time step. The second clause says that, whenever a chicken lays an egg at position "Pos", it must trigger an event called "spawn" with 3 parameters:
(1) The ID of the actor which triggered the "spawn" event (i.e. the ID of the chicken),
(2) The name of the event which caused the "spawn" event (i.e. "layEgg"), and
(3) The position at which the egg is supposed to spawn (i.e. Pos).
The "spawn" event, then, will complete the spawning process (of the egg) by invoking the "spawned" event. This is where the ID generation takes place. As you can see in the first argument of "spawned(...)", the rule basically creates a brand new symbol (i.e. a string literal) by concatenating the 3 existing symbols - the integer which denotes the current time, the ID of the source, and the name of the cause of the spawning process. This is the ID of the new actor (i.e. egg), and it is guaranteed to be unique because each chicken can only trigger up to one "layEgg" event at a time.
(Note: Think of the notation "{n}_{Src}_{Cause}" as an instance of string interpolation which you can see in many programming languages including C#, Javascript, etc. I am supposing here that the Prolog interpreter is capable of creating new symbols (string-based literal expressions) based off of any interpolated strings and memorizing them.)
Now, for instance, if the following event occurs:
spawned[16](16_foo_layEgg, foo, layEgg, <3, 4>)We will be able to tell that at time [n = 16], chicken "foo" gave birth to an egg called "16_foo_layEgg" at position <3, 4>.
One may argue that such a method of spawning actors feels a bit too restrictive, since it does not seem to allow the chicken to lay more than one eggs at each time step. A game designer might ask, "Hey, what if I want to create a special magic spell which lets a chicken lay 2 or 3 eggs at once, instead of just 1?"
The solution is pretty simple. You just come up with more types of events to be able to trigger the spawning of extra eggs, like the ones listed below.
layEgg[n](X) :- chicken[n](X).
layEgg2[n](X) :- chicken[n](X), extraEggBoost[n](X, NumExtra), greaterThan(NumExtra, 0).
layEgg3[n](X) :- chicken[n](X), extraEggBoost[n](X, NumExtra), greaterThan(NumExtra, 1).
spawn[n](X, layEgg, Pos) :- layEgg[n](X), position[n](X, Pos).
spawn[n](X, layEgg2, Pos) :- layEgg2[n](X), position[n](X, Pos).
spawn[n](X, layEgg3, Pos) :- layEgg3[n](X), position[n](X, Pos).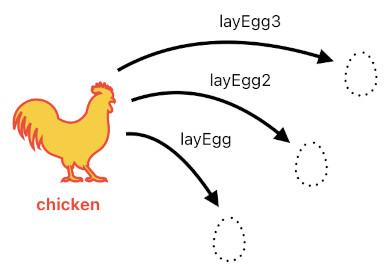
Suppose that the "extraEggBoost" predicate denotes the presence of that magic spell the designer talked about, under the assumption that "X" is the ID of the chicken and "NumExtra" indicates the number of extra eggs that the chicken is required to lay each time the clock ticks. The rules above, then, show us that the following three scenarios are possible depending on what the value of "NumExtra" is:
(1) If either NumExtra is 0 or "extraEggBoost(X, NumExtra)" does not even exist for X (meaning that chicken X is currently not endowed with any active extra-egg spell), only "layEgg" will be triggered.
(2) If NumExtra is at least 1, both "layEgg" and "layEgg2" will be triggered.
(3) If NumExtra is at least 2, both "layEgg" and "layEgg2", as well as "layEgg3", will be triggered.
And since "layEgg", "layEgg2", and "layEgg3" are distinct types of events which will separately contribute to the same chicken's egg-spawning process (since they belong to 3 different causes and thus generate 3 different IDs), we can modulate the number of simultaneously spawnable eggs by activating a subset of these 3 events.
If a chicken called "foo" gave birth to 3 eggs at time 16 and position <3, 4>, for example, the following three events will be invoked. As you can clearly see, all of these 3 eggs are given unique IDs because they all originated from unique causes (i.e. layEgg, layEgg2, and layEgg3).
spawned[16](16_foo_layEgg, foo, layEgg, <3, 4>)
spawned[16](16_foo_layEgg2, foo, layEgg2, <3, 4>)
spawned[16](16_foo_layEgg3, foo, layEgg3, <3, 4>)At this point, a programmer might come over and say, "Dude, what if we want to allow the chicken to lay hundreds of eggs instead of just a handful? Do you expect me to write hundreds of lines of code?" Such a concern, too, can be resolved without too much hassle. All we have to do is stop treating every single egg as an individual actor.
What I mean by this is that we are not obliged to give a unique ID to every egg (It will be quite detrimental to the system's performance if we do that to hundreds of eggs anyways). Instead, we could just create an actor which represents a group of multiple eggs.
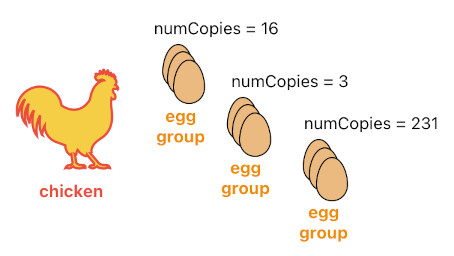
This approach will work as long as it is not necessary to separately keep track of each egg. The only thing we need to do is convert the "Cause" argument of the spawning process into a vector, and pass the number of eggs as its second component. The resulting "numCopies" attribute, then, will signify the number of eggs within the spawned egg-group object. Its code implementation is displayed below.
layEggs[n](X, 1) :- chicken[n](X).
layEggs[n](X, NumEggs) :- chicken[n](X), extraEggBoost[n](X, NumExtra), add(1, NumExtra, NumEggs).
spawn[n](X, <layEggs, NumEggs>, Pos, NumEggs) :- layEggs[n](X, NumEggs), position[n](X, Pos).
spawned[n]("{n}_{Src}_{Cause}", Src, Cause, Pos) :- spawn[n-1](Src, Cause, Pos).
numCopies(Id, NumCopies) :- spawned[n](Id, Src, Cause, Pos), y(Cause, NumCopies).(Will be continued in Part 8)
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service