
Author: Youngjin Kang Date: September 7, 2024
This is Part 5 of the series, "Game Programming in Prolog". In order to understand what is going on in this article, please read Part 1 first.
So far, I have explained how the concept of space and time could be represented in the language of Prolog. These two are inarguably the most fundamental backbones of a gameplay sytem, for otherwise the range of things which the gamer is able to do would be extremely limited (Lack of time means absence of progression, and lack of space means absence of visual/physical elements).
The very presence of space and time, however, does not automatically give us toys to play with. A game is an interactive medium; it needs to have interactions between the player and the rest of the game world, as well as interactions within the world itself. A great game is a system which involves a rich network of such interactions.
Fortunately, devising interactions in Prolog is fairly straightforward (perhaps even more so than in an imperative language), due to the fact that each of them can be defined as a mapping of one set of relations to another. This is exactly what Prolog is designed for.
Let us begin with one of the most rudimentary forms of interactions - collision. When two actors get sufficiently close to each other, they collide.
The very definition of collision depends on what kind of physics we have in our minds. It could vary depending on whether the space is discrete or continuous, whether the game is turn-based or in real time, and so forth. For the sake of convenience, though, I will simply assume here that two actors "collide" whenever they are located at the same position (defined below).
collide(X[n], Y[n]) :- position(X[n], P), position(Y[n], P).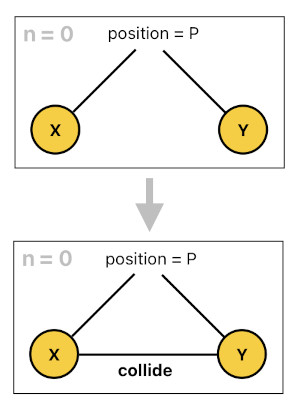
Now, we know how to tell at which moment a pair of actors happen to collide. The predicate "collide(X[n], Y[n])" tells us that actor X and Y collide at time 'n'. Let us decide what to do when this happens.
A great example of an interaction could be found in the context of resource gathering. Imagine that there is a creature which is capable of feeling hunger (i.e. possesses a "hunger" stat). It feels hungry whenever its hunger level gets sufficiently high. And whenever it feels hungry, it eats any food that is nearby.
The following code is an implementation of the logic I just mentioned. The first rule states that any actor must be considered "hungry" whenever its hunger level becomes greater than 5, and the second rule states that a hungry actor must eat any colliding object which is edible.
hungry(X[n]) :- hunger(X[n], H), greaterThan(H, 5).
eat(X[n], Y[n]) :- hungry(X[n-1]), canEat(X[n-1], Y[n-1]), collide(X[n-1], Y[n-1]).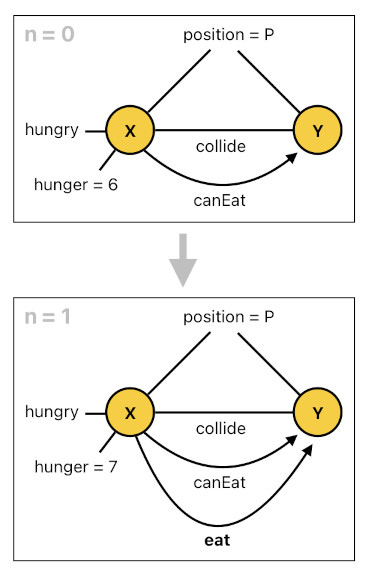
This will guarantee that, once you drop a food (i.e. anything which can be eaten) right at the spot at which a hungry creature is located, the creature will devour it.
Here is another example, which more thoroughly demonstrates the notion of emergence in gameplay. Suppose that there are two actors named "actor1" and "actor2". The first actor represents fire, the second actor represents a piece of bread, and they were both spawned at the same exact time and place (see the code below).
fire(actor1).
bread(actor2).
spawnTime(actor1, 0).
spawnTime(actor2, 0).
spawnPosition(actor1, <0, 0>).
spawnPosition(actor2, <0, 0>).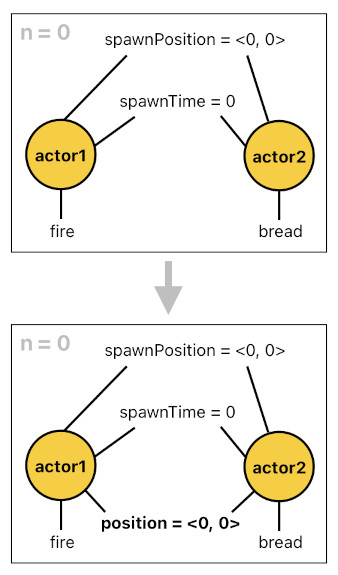
Since these two actors are equipped with their own identities (i.e. "fire" and "bread"), we are able to formulate an identity-based rule of interaction between them. For instance, we may come up with a clause which says that a fire should burn any piece of bread it happens to touch.
burn(X[n], Y[n]) :- fire(X[n-1]), bread(Y[n-1]), collide(X[n-1], Y[n-1]).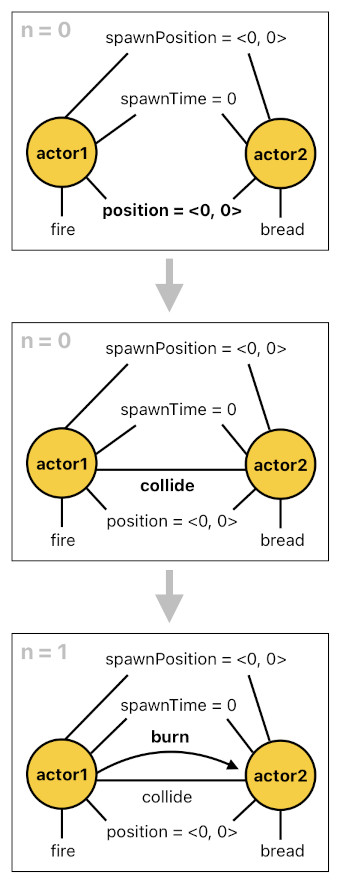
Here is the catch, though. First of all, bread is not the only type of object which can be burned by fire; there are innumerable things in our world which are supposed to be burned when they get exposed to fire. Furthermore, fire is not the only type of object which is capable of burning other things; lava, oven, death ray, and myriad other sources of intense heat all possess such an ability.
What we need here is a "general rule" as opposed to a specific rule. For sure, you wouldn't want to be writing a bunch of rules which are mere variants of the same underlying pattern, like the ones listed below.
burn(X[n], Y[n]) :- fire(X[n-1]), bread(Y[n-1]), collide(X[n-1], Y[n-1]).
burn(X[n], Y[n]) :- fire(X[n-1]), tree(Y[n-1]), collide(X[n-1], Y[n-1]).
burn(X[n], Y[n]) :- fire(X[n-1]), paper(Y[n-1]), collide(X[n-1], Y[n-1]).
burn(X[n], Y[n]) :- lava(X[n-1]), bread(Y[n-1]), collide(X[n-1], Y[n-1]).
burn(X[n], Y[n]) :- lava(X[n-1]), tree(Y[n-1]), collide(X[n-1], Y[n-1]).
burn(X[n], Y[n]) :- lava(X[n-1]), paper(Y[n-1]), collide(X[n-1], Y[n-1]).
...A rule which is generic enough to cover all these specific cases will be way more desirable. This leads us to the idea of tagging actors not only with their specific identities (such as "fire" and "bread"), but also with their general properties (e.g. adjectives).
For example, fire, lava, and oven are "similar" in the sense that they are all hot. This means that they all share the same general property called "hot".
In the same spirit, we may claim that bread, tree, and paper are "similar" in the sense that they are all flammable. This means that they all share the same general property called "flammable".
hot(X) :- fire(X).
hot(X) :- lava(X).
hot(X) :- oven(X).
flammable(X) :- bread(X).
flammable(X) :- tree(X).
flammable(X) :- paper(X).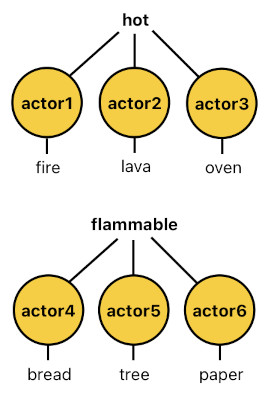
Mathematically speaking, such a grouping mechanism may as well be thought of as a process of defining sets. That is, it could be said that fire, lava, and oven are elements of the set called "hot", while bread, tree, and paper are elements of the set called "flammable".
The main advantage of doing this is that it allows us to define a general rule which states that any hot object should be able to burn any flammable object it happens to touch. It does not matter whether the hot object is fire, lava, or oven, and it does not matter whether the flammable object is bread, tree, or paper. As long as there is something hot and something flammable colliding with each other, we will be able to tell that the former will burn the latter.
burn(X[n], Y[n]) :- hot(X[n-1]), flammable(Y[n-1]), collide(X[n-1], Y[n-1]).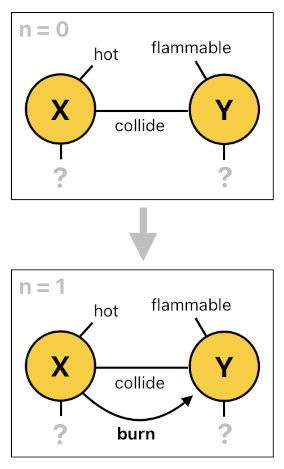
So, there you have it. This single rule covers all possible permutations between the potential sources of burn ("fire", "lava", "oven") and their potential targets ("bread", "tree", "paper"). Even if the designer happens to come up with hundreds (or even thousands) of unique object names, this mechanic will still work flawlessly as long as hot objects are labeled as "hot" and flammable objects are labeled as "flammable".
This is not the end of the story, though. Note that nothing prevents us from attaching more than just a single property (e.g. adjective) to an actor; we are allowed to attach as many as we want, reflecting the multifacetedness of the actor's characteristics.
For example, a piece of bread is not only flammable, but is also a source of food for human beings (Note: Even someone who is fatally allergic to it can still manage to eat it at least once in his/her lifetime, so there is no logical contradiction here). This means that we should attach two different tags to each bread actor - "flammable" and "foodForHuman".
This allows each piece of bread to interact with two distinct types of actors - those which are identified as "hot", and those which are identified as "human". When something hot (such as fire) touches the bread, it will be burned. But when a hungry person touches the bread, it will be eaten. Two alternative responses, depending on which tag is associated with which interaction!
flammable(X) :- bread(X).
foodForHuman(X) :- bread(X).
canBurn(X[n], Y[n]) :- hot(X[n]), flammable(Y[n]).
burn(X[n], Y[n]) :- canBurn(X[n-1], Y[n-1]), collide(X[n-1], Y[n-1]).
canEat(X[n], Y[n]) :- human(X[n]), foodForHuman(Y[n]).
eat(X[n], Y[n]) :- hungry(X[n-1]), canEat(X[n-1], Y[n-1]), collide(X[n-1], Y[n-1]).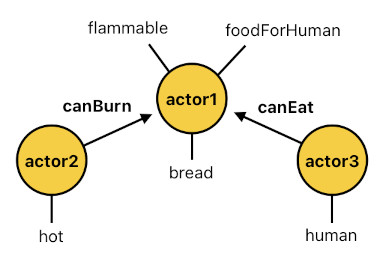
Adding more and more tags to our actors will exponentially increase the number of ways in which they may interact. This is the kind of emergence we want in video games, especially ones whose main source of entertainment originates from "mix and match" mechanics such as crafting rules, puzzles, etc.
Not all interactions are instantaneous, though. Sometimes, games involve interactions which take effect after some delay. Think of a war game in which the soldiers attack each other by shooting projectiles such as bullets, arrows, and rocks.
For the case of bullets, we may simply assume that there is no delay at all because a bullet is so fast that no one is able to feel any noticeable delay. It is not the case with much slower projectiles such as arrows and rocks. They take considerably more time to reach their targets, and we must take this into account when implementing games.
Fortunately, delays of any reasonable length can be implemented fairly easily by doing a bit of arithmetic. Recall that 'n' indicates the current time step and 'n-1' indicates the previous time step. Likewise, 'n-2' must indicate 2 steps in the past, 'n-3' must indicate 3 steps in the past, and so on.
This means that, if a projectile takes N time steps to hit the target, the "hitting" event must occur at the current time step (n) if and only if the projectile was fired at time 'n-N'. So, if we assume that a bullet takes 1 time step, an arrow takes 3 time steps, and a rock takes 5 time steps to reach the destination, we could formulate such delays by specifying rules as shown below:
hit(Y[n], Projectile[n]) :- shoot(X[n-1], Y[n-1], Projectile[n-1]), bullet(Projectile).
hit(Y[n], Projectile[n]) :- shoot(X[n-3], Y[n-3], Projectile[n-3]), arrow(Projectile).
hit(Y[n], Projectile[n]) :- shoot(X[n-5], Y[n-5], Projectile[n-5]), rock(Projectile).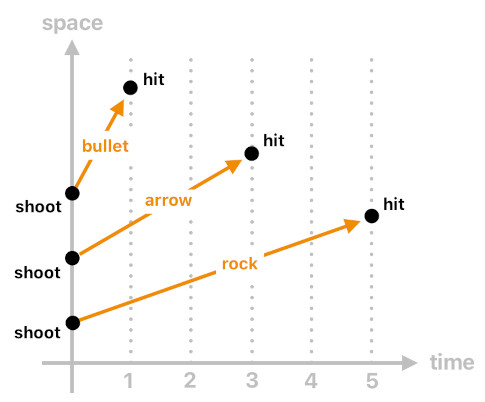
It is also possible to design a number of interesting game mechanics out of this. A good example can be found in the case of a boomerang, which reaches the target AND comes back to its owner after some additional delay. The following code implements such a mechanic.
hit(Y[n], Projectile[n]) :- shoot(X[n-2], Y[n-2], Projectile[n-2]), boomerang(Projectile).
hit(X[n], Projectile[n]) :- shoot(X[n-4], Y[n-4], Projectile[n-4]), boomerang(Projectile).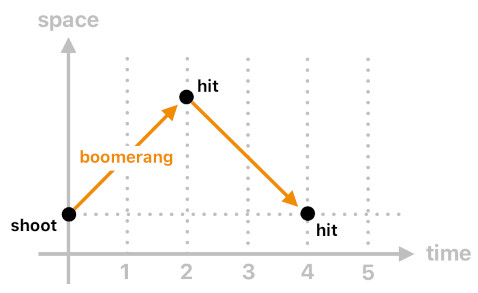
But of course, these simple rules may not suffice for nuanced gameplay. A projectile might need to be "interceptable" while its movement is still in progress. For instance, a flying rock should be able to change its trajectory due to a sudden force of knockback summoned by a wizard, etc.
This problem can be solved by constructing definitions on a step-by-step basis. Instead of waiting for 5 clock cycles and then raising the "hit" event, for example, a rock may initiate a chain of "motionProgress" events throughout the course of its 5-step movement. Each of these intermediary events, then, would be triggered by the preceding "motionProgress" event which was invoked just one clock cycle ago, not 5. The code below demonstrates how it can be done.
(Note: The fact that these rules only look up 1 step in the past, instead of 5, implies that the computer will no longer be obliged to store 5 past snapshots of the game in its memory. This is a nice way of saving computational resources.)
motionProgress(rock, Y[n], Projectile[n], 0.0) :- shoot(X[n], Y[n], Projectile[n]), rock(Projectile).
motionProgress(rock, Y[n], Projectile[n], 0.2) :- motionProgress(rock, Y[n-1], Projectile[n-1], 0.0).
motionProgress(rock, Y[n], Projectile[n], 0.4) :- motionProgress(rock, Y[n-1], Projectile[n-1], 0.2).
motionProgress(rock, Y[n], Projectile[n], 0.6) :- motionProgress(rock, Y[n-1], Projectile[n-1], 0.4).
motionProgress(rock, Y[n], Projectile[n], 0.8) :- motionProgress(rock, Y[n-1], Projectile[n-1], 0.6).
motionProgress(rock, Y[n], Projectile[n], 1.0) :- motionProgress(rock, Y[n-1], Projectile[n-1], 0.8).
hit(Y[n], Projectile[n]) :- motionProgress(rock, Y[n], Projectile[n], 1.0).Want to be able to interrupt the rock's motion in the midst of its trajectory? No problem. All we need to do is add an extra condition to each of these rules which tells the system to terminate the chain of "motionProgress" if the rock was interrupted during the previous time step. The amended rules are listed below.
motionProgress(rock, Y[n], Projectile[n], 0.0) :- shoot(X[n], Y[n], Projectile[n]), rock(Projectile).
motionProgress(rock, Y[n], Projectile[n], 0.2) :- !interrupt(Projectile[n-1]), motionProgress(rock, Y[n-1], Projectile[n-1], 0.0).
motionProgress(rock, Y[n], Projectile[n], 0.4) :- !interrupt(Projectile[n-1]), motionProgress(rock, Y[n-1], Projectile[n-1], 0.2).
motionProgress(rock, Y[n], Projectile[n], 0.6) :- !interrupt(Projectile[n-1]), motionProgress(rock, Y[n-1], Projectile[n-1], 0.4).
motionProgress(rock, Y[n], Projectile[n], 0.8) :- !interrupt(Projectile[n-1]), motionProgress(rock, Y[n-1], Projectile[n-1], 0.6).
motionProgress(rock, Y[n], Projectile[n], 1.0) :- !interrupt(Projectile[n-1]), motionProgress(rock, Y[n-1], Projectile[n-1], 0.8).
hit(Y[n], Projectile[n]) :- motionProgress(rock, Y[n], Projectile[n], 1.0).(Will be continued in Part 6)
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service