
Author: Youngjin Kang Date: September 2, 2024
This is Part 3 of the series, "Game Programming in Prolog". In order to understand what is going on in this article, please read Part 1 first.
So far, I have shown how the parameterization of time steps can indeed be a powerful tool for triggering state transitions in the system. In order to better understand the reasoning behind this, however, we ought to take a step back and really try to see the overall picture of what is going on behind the formulas.
Whenever we are dealing with the system's state and its means of transition, we are essentially thinking in terms of causes and their corresponding effects. A horn clause, for instance, is a rule which tells us what kind of effect can be generated based upon a given set of causes, just as illustrated below.
effect(...) :- cause1(...), cause2(...), cause3(...).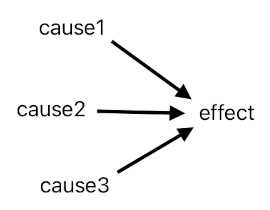
A nice way of visualizing such a causal phenomenon is to imagine each of the predicates (i.e. either a cause or effect) as a point in spacetime.
Spacetime is simply a dimensional representation of the game's history; it consists of spatial axes as well as a time axis. When you throw a rock in the upward direction, for example, you will be able to plot its trajectory in spacetime as a parabola (because it will rise, stop, and fall).
Here is the catch, though. An effect is a product of causes, yet such an effect itself may as well be a cause of another effect. Thus, it does not quite make sense to try to establish a strict distinction between causes and effects. Depending on how our causal chains are interwoven, an effect could as well be identified as a cause and vice versa.
A unifying terminology between cause and effect is "event". Our spacetime is filled with events; each point in spacetime is an event, and an directed line segment (i.e. arrow) between two points in spacetime is a causal connection which leads one event to another. The code below is an example of a horn clause which defines "event3" as a product of two such connections (one between "event1" and "event3", and the other one between "event2" and "event3"). Here, "event1" and "event2" are the causes of "event3", and "event3" is the effect of "event1" and "event2".
event3(...[n]) :- event1(...[n-1]), event2(...[n-2]).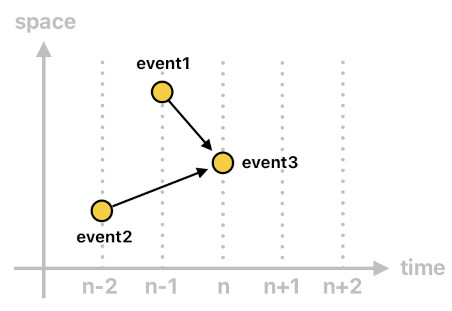
In general, our gameplay system can be thought of as a collection of causal rules, each of which specifies a type of event which can be generated out of a set of preceding events. These rules, as they get applied to the game loop over and over as time elapses (in a periodic manner), gradually map out the fabric of causal connections in spacetime, revealing us the full picture of which events are related to which. This implies that the full history of the gameplay itself can be modeled as an "event graph" - an instance of a DAG (Directed Acyclic Graph), which is reminiscent of the so-called "blockchain", "hashgraph", and other event sourcing protocols.
"But," someone might say, "But! Don't you think that not all predicates represent events? If a horn clause happens to contain a relation called 'bread(X)', for instance, it must be obvious that this particular relation simply serves as a tag which declares that X is a piece of bread. It is by no means an event; it is just an indicator, and nothing more than that."
Such a line of thought definitely makes sense from a layman's point of view. An indicative relation such as "bread(X)", as it comprises a simple noun, is indeed something which feels hardly anything more than a mere semantic reference. From a strictly spacetime-oriented perspective, however, one must be able to consider every logical predicate as an event, even if it happens to serve as an identifier.
Let me show you an example. Suppose that there is an arbitrary hydrogen atom called "X". The identity of such an atom can be described by the code below:
hydrogen(X).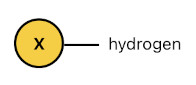
What this relation really means, though, is: "There is an atom called 'X' which can be identified as 'hydrogen' at every moment of its existence". Thus, a more comprehensive means of expressing this relation would be the one shown below:
hydrogen(X[n]) :- spawnTime(X, n).
hydrogen(X[n]) :- hydrogen(X[n-1]).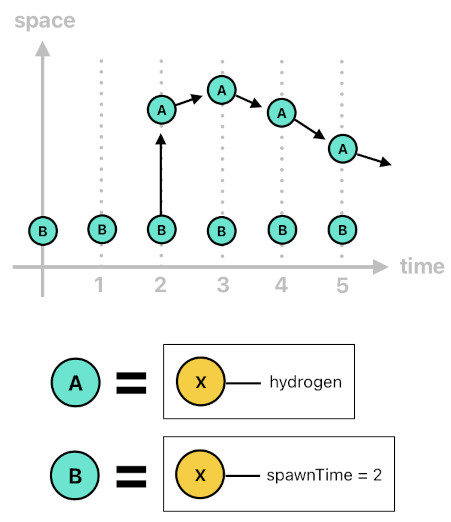
The true meaning of "hydrogen(X)" is that there is a chain of events in spacetime which consistently keep telling us that there has been a hydrogen atom called "X", whose line of existence began at X's moment of birth (aka "spawnTime") and has henceforth been growing itself through the passage in time. The first horn clause establishes the base case (i.e. first occurrence of the "hydrogen" event), and the second horn clause establishes the recursive case which generates the succeeding chain of "hydrogen" events.
In a way, therefore, a simple name tag such as "hydrogen(X)" can be interpreted as a connected sequence of points (events) in spacetime. The key takeaway here is that the very concept of "object" (i.e. a distinct body of existence) itself should be understood as a line in the hyperdimensional geometry of our universe, similiar to what physicists refer to as a "world line" - a four-dimensional path of an object in spacetime.
And of course, when individual atoms bond with one another, they form a molecule. Such a molecule, too, can be considered a discrete object with its own line of existence in spacetime.
An example case is demonstrated below. When two hydrogen atoms (X, Y) and an oxygen atom (Z) bond, they altogether form a water molecule. In this case, the birth of the water molecule (which is an event) may as well be considered an effect which was produced by the four causes listed below:
(1) The existence of the first hydrogen atom X at time n-1.
(2) The existence of the second hydrogen atom Y at time n-1.
(3) The existence of the oxygen atom Z at time n-1.
(4) The bonding of the aforementioned three atoms at time n-1.
water(X[n], Y[n], Z[n]) :- hydrogen(X[n-1]), hydrogen(Y[n-1]), oxygen(Z[n-1]), bond(X[n-1], Y[n-1], Z[n-1]).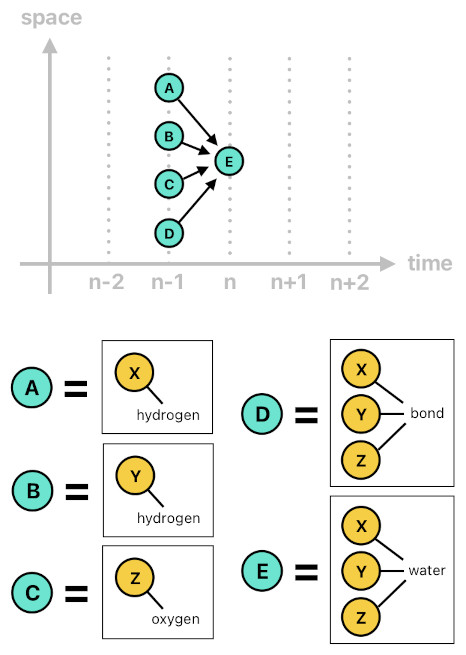
The inverse scenario of the bonding process is the act of split, which in this case can be depicted as the splitting of the water molecule into its individual component atoms (2 hydrogens and 1 oxygen). This, too, should be able to be rendered as a set of causal connections between events, just as shown below.
hydrogen(X[n]) :- water(X[n-1], Y[n-1], Z[n-1]), split(X[n-1], Y[n-1], Z[n-1]).
hydrogen(Y[n]) :- water(X[n-1], Y[n-1], Z[n-1]), split(X[n-1], Y[n-1], Z[n-1]).
oxygen(Z[n]) :- water(X[n-1], Y[n-1], Z[n-1]), split(X[n-1], Y[n-1], Z[n-1]).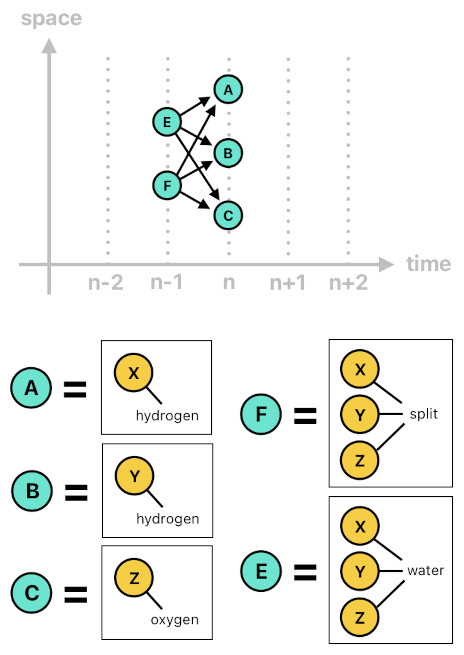
A Prolog-based gameplay system is extremely straightforward in nature, if you think about it for a second. In this virtual universe, everything is an event and events are causally related to each other via horn clauses (aka "rules").
As time passes by, events which are sufficiently old (i.e. so old that they no longer influence any of the future events) get discarded because they are obsolete. Meanwhile, the game loop keeps ticking its clock, generating new events in spacetime (i.e. those which belong to time 'n'). These new events get registered to the memory, while the oldest ones get thrown away. This means that there is a "window of remembrance" in spacetime which covers events that are fairly recent (see the image below).
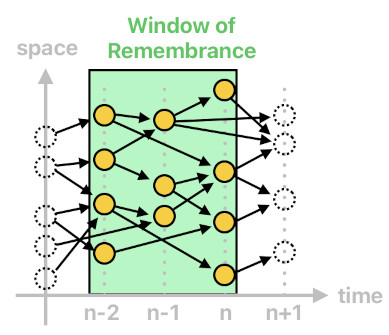
Events which fall within this window are the ones which are being kept in the computer's memory. As old events get discarded (i.e. exit the window through the left edge), their corresponding memory slots get freed up. And as new events get created (i.e. enter the window through the right edge), they get stored in these freed up slots. Thus, the same array of memory slots get recycled over and over again, just like in any other dynamic memory allocation system. This proves that Prolog is a sound choice even from the perspective of memory optimization.
(Note: If you force every event to occupy the same exact amount of space in memory, you will be able to simplify the allocation scheme even further because the system will only need to keep track of free slot indices, not how large those free slots are.)
Here is something I would like to point out before proceeding to the next chapter. The model of spacetime which I have explicated by far is a strictly Newtonian one, meaning that every "present event" is nicely aligned within the same exact time step (i.e. "n"). This is because all present events get generated by the gameplay system in a completely synchronous (aka "lockstep") manner. Here, time is an independent variable and we can easily tell which events are simultanous with each other and which ones are not. If two or more events belong to the same time step, they must be considered simultaneous.
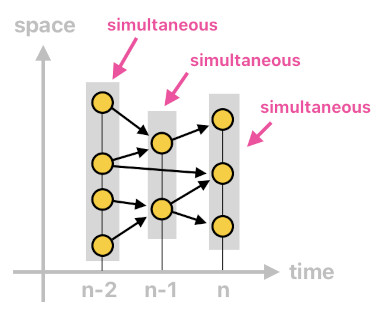
When a multitude of game loops (i.e. threads) are running concurrently, however, we can no longer easily tell which events are simultaneous with which. Besides, the presence of multiple game loops implies the presence of multiple clocks running independently, suggesting that we cannot even be sure which events belong to the "present moment" and which ones do not (because there would be more than a single frame of reference in time).
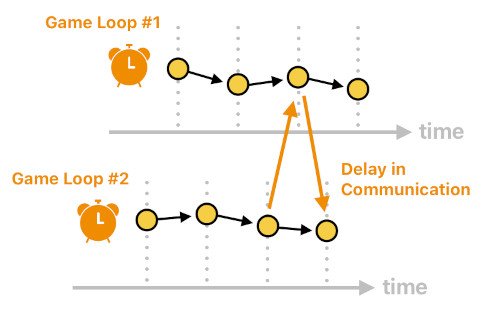
Furthermore, depending on the order in which the game loops update themselves and which clusters of events they happen to be updating at each clock cycle, there is likely to be some kind of "propagation delay" among the events' forces of influence (due to the limit in the speed of light - the maximum rate at which information travels in space).
Such lack of simultaneity in events and their causal connections inevitably forces us to reimagine space as a fabric of causal relations (i.e. event graph), rather than a fixed coordinate system (i.e. Euclidean space) in which the notion of time can simply be expressed as an independent dimension.
This apparent lack of absolute synchronicity among events, introduced by the coexistence of multiple concurrent event-generating processes of the universe, reminds us of two analogous topics in academia, one of which belongs to computer science and the other one of which belongs to modern physics.
In computer science, the aforementioned notion of concurrency is considered the main source of many time-related algorithmic errors such as race conditions, where the evil can be attributed to the misordering of operations (which is quite common in imperative programming) which may have been caused not only by the programmer's coding mistake, but also by the lack of certainty in the speed at which the result of operation gets broadcasted from thread to thread.
In modern physics, concurrency of events and their apparent lack of ability to sync up instantly (due to the fact that their waves of influence cannot move faster than light) comprise one of the core pillars of Einstein's Theory of Relativity, where space and time can be "warped" based on the way in which events are causally connected.
In the case of a single-threaded gameplay system, though, we do not have to worry about any of the aforementioned perils of asynchronicity. As long as our Prolog program sticks its mode of operation to a single game loop, we will be safe from any of the bizarre relativistic effects such as time dilation, etc. This also means that we may imagine the game world as a simple Newtonian model of spacetime, in which the spatiotemporal location of every event can be specified in terms of Cartesian coordinates.
The only potential source of error in a single-threaded Prolog application is the very logical ambiguity in the code itself, and nothing else. As long as the rules (i.e. horn clauses) are formulated in a manner which won't allow a loophole (such as unintended reliance on the order of operation), everything is going to be fine. An example of such an undesirable loophole is demonstrated below.
carryUmbrella(Person[n]) :- rainy(City[n]), resident(Person[n], City[n]).
rainy(City[n]) :- cloudy(City[n-1]).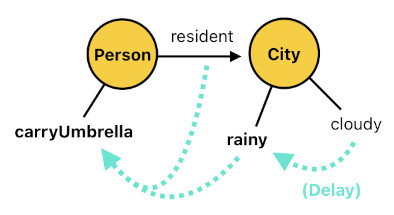
This scenario tells us that, whenever a city gets cloudy, it must be rainy at the next time step. This is fine so far.
It also tells us that a rainy city must instantly make its residents carry umbrellas without any time delay. But alas! The rule which enforces the carrying of umbrellas is written BEFORE the rule which updates the "rainy" status of the city, which means that, by the time the city gets tagged as "rainy", the "carryUmbrella" rule would have already been examined and ignored.
This is the kind of race condition which may occur if we do not take sufficient care when ordering horn clauses whose lefthand and righthand sides both reference the same time step (i.e. "n"). There are multiple ways of preventing this kind of error, such as:
(1) Forcing the Prolog interpreter to scan the list of rules twice instead of just once, so that the "carryUmbrella" predicate will be recognized and be activated during the second scan (because the "rainy" predicate would have been activated by the end of the first scan), or,
(2) Just writing the rules in the correct order.
Both of these solutions will work, although they both involve their own tradeoffs. The first solution allows the two horn clauses to be written in any order, yet the necessity of scanning the whole code multiple times decreases the efficiency of the program. The second solution is great for efficiency, yet it requires extra care when writing the code.
(Will be continued in Part 4)
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service