
Author: Youngjin Kang Date: July 28, 2024
When developing a game, one of the biggest challenges that the developer often encounters is the problem of implementing complex gameplay systems.
A large-scale game project often involves various in-game events, such as instantaneous actions (e.g. malee attack), firing of projectiles, casting of spells (i.e. status conditions), area effects, upgrades, and many others. It is not so easy to make sure that all these events will coexist in harmony, due to undesired side effects which might be caused by factors such as: (1) Race condition, (2) Combination of multiple events, (3) Criteria for deciding whether an event should be applied or not, and so on.
Professor Gärdenfors, who is both a cognitive scientist and a philosopher at the University of Lund (Sweden), has introduced a structurally elegant model of events and their internal causal relations. It is called the "Two-Vector Model", and it leverages vector quantities as means of specifying the cause and effect of an event. In other words, his model defines an event as an instance of vector transformation.
What I have personally noticed is that his event model works beautifully in the context of game development. Many of the complexities which are prone to arise in gameplay systems can easily be mitigated (or even avoided) by applying the two-vector model, due to the fact that it lets us nicely encapsulate each gameplay event's causal relation as a simple algebraic operation.
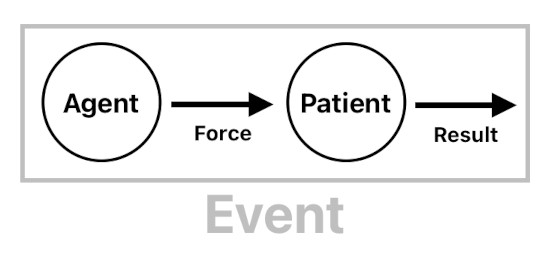
According to Professor Gärdenfors' definition of cause and effect, an event can be thought of as a vector function which takes a vector as the input and returns another vector as the output.
In the two-vector event model, the input is a "force vector" and the output is a "result vector". Imagine that there are two separate entities in the world - agent and patient. The agent is the one who causes the event, and the patient is the one who is being affected by the event. Once the event kicks in, the patient receives the force vector (aka "cause") that was emitted by the agent, and yields its own result vector (aka "effect").
The result vector should be able to represent any type of change, but the easiest way to understand it (from the point of view of classical mechanics) is to simply assume that it represents an offset in the patient's position. So if you (i.e. agent) hit a ball (i.e. patient) with the force of 1N and let it move by 1m, you may say that the force vector is (1N, 0N, 0N) and the result vector is (1m, 0m, 0m) in 3D space.
Gärdenfors, however, does not necessarily confine the force and result vectors solely to the physical domain. In his model of events, a "position" may as well refer to the quality of the patient (e.g. color, temperature, emotional state, etc), and a "force" may as well be considered a force which modifies the quality. For instance, an act of painting can be considered an application of a "color-changing force" to the patient, which subsequently pushes the patient's position in color space (e.g. RGB) to the desired color location.
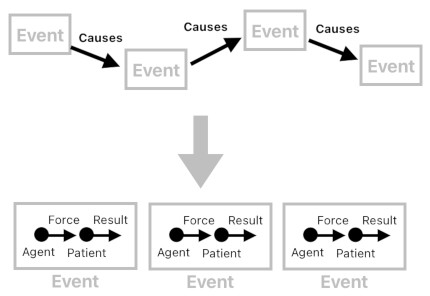
Gärdenfors' event model differs from more traditional models of causation due to its nature of self-encapsulation. It has widely been presumed that the so-called "causation" is simply a relation between events, and that each event is more or less just a "snapshot" of how things look like at each moment. In Gärdenfors' model, on the other hand, each event contains its own cause-and-effect relation, defined in terms of agent, patient, force, and result. The agent and the force it emits can altogether be considered the "cause" of the event, while the patient and its result of receiving the emitted force can altogether be considered the "effect" of the event.
I think the most prominent advantage of modeling an event this way is that it allows us to apply the notion of causation inside the event itself rather than in terms of its relation with other events. In computer science, such a form of conceptualization nicely fits the OOP (Object-Oriented Programming) paradigm, where each object defines its own behaviors within its own body. So for example, in a typical object-oriented programming language such as Java or C#, it is oftentimes convenient to define "Event" as a class, and assume that its force-to-result vector transformation procedure (i.e. causal relation) will be implemented as the class's member function.
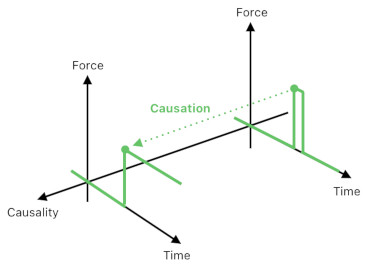
As a side note, I would like to briefly introduce yet another mathematical interpretation of an event. In his paper on event structure and force dynamics (See Fig 11 of "Event structure, force dynamics and verb semantics"), Gärdenfors explains Croft's alternative definition of causality. According to Croft, a cause-and-effect relation between forces can be explicated as the propagation of a "causal signal" across the dimension of causality. What's really interesting in this worldview is that it imagines "causality" as yet another dimension in spacetime, via which various worldly phenomena (i.e. events) establish causal links with one another.
This philosophically fascinating design, however, requires both the force vector and the result vector to reside in the same set of dimensions, thereby disallowing the result vector from identifying itself as part of its own hypothetical space which is of a different type from that of the force vector. This apparent lack of expressive freedom, I think, is one of the reasons why this unified spatial representation of causality is not so widely used.
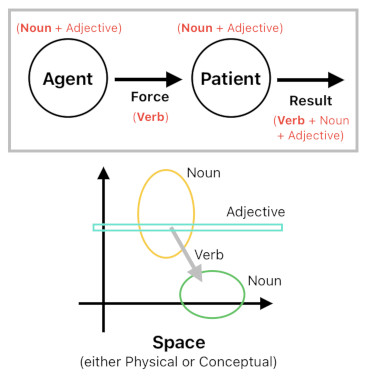
In "Causal Reasoning and Event Cognition as Evolutionary Determinants of Language Structure", as well as the latter half of "Event structure, force dynamics and verb semantics", Gärdenfors suggests a possible usage of his two-vector event model as a device for explaining sentence structures in our language. An "event", according to him, can be expressed as an English sentence because it has its own subject (agent), verb (force), and object (patient).
Both the agent and patient can be described by nouns, yet adjectives and prepositions can also be leveraged as "filters" for specifying them more precisely. For example, in conceptual space (aka "feature space" in machine learning and artifical intelligence), a noun can be imagined as a voluminous region (which encloses a cluster of data points that are associated with that noun) and an adjective can be imagined as a thin plane which partially intersects such a region. A combination between a noun and an adjective (e.g. "black cat", "white rose", or "wooden jar"), therefore, indicates the intersection (i.e. a plane segment) between the noun's region and the adjective's plane.
Similarly, a preposition may as well function as a filter because it specifies a region in physical space with respect to the physical location (and direction) of the observer's point of reference. It "sorts out" any object which does not fall within the specified region.
The force and result vectors are expressible in terms of verbs. Here, a verb (or a "verb phrase" in general) can be defined as a vector transformation which maps a region in space to another region in space. These regions are specified by the sentence's subject and object, respectively.
Based upon these observations, Professor Gärdenfors suggests that we formulate our language in terms of events and their force-to-result (i.e. cause-and-effect) relations. In other words, our language is based on the way we cogitate causal relations.
A potential application of Peter Gärdenfors' event model can be found in the development of video games. When designing a gameplay system, a developer often finds it hard to construct the cause-and-effect relations of various in-game events (e.g. Attack, Heal, Stun, Knockback, Poison, Teleport, etc) without introducing too many layers of complexity. Gärdenfors' nicely encapsulated model of events solves this problem, and I am here to demonstrate why.
First of all, we need to take a look at the generalized form of the two-vector model in order to be able to leverage it for game design purposes. It is illustrated below.
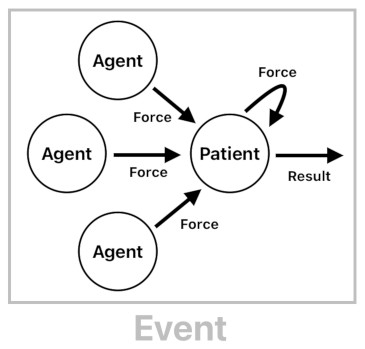
Previously, I have shown that an event can be summarized as a combination of a cause (i.e. agent and the force it emits) and an effect (i.e. patient and the result it generates from the received force). In general, however, an event does not necessarily have to involve exactly one agent, one patient, and one force vector.
Whenever I walk on my own, I am both the one who exerts the force of movement (agent) and the one who is being moved by that force (patient). And whenever I happen to be pushed by two people simultaneously, I should consider both of them as the agents of the "push" event. Their force vectors will have to be added up to yield the net force vector, which will then be used by the event to compute the result vector.
Let me show you a simple gameplay scenario to explain why the concept shown so far is useful for gameplay systems design. Suppose that there is a role-playing game in which the player is a fantasy warrior traveling in a dungeon. There are currently 3 characters nearby, one of them attacking the player (i.e. Attacker) and the other two healing the player (i.e. Healer A and Healer B). The player has a health bar which shows his current health. Each attacker decreases the health, and each healer increases the health.
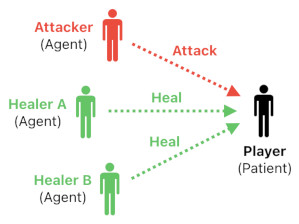
In the two-vector model, it is necessary to represent this simultaneous presence of attacking/healing effects as a combination of force vectors. Imagine that there is a hypothetical space called "force space" in which all the contributing forces of the event reside (The idea of representing the force/result vectors in their own conceptual spaces is illustrated in "Event structure, force dynamics and verb semantics"). When an event kicks in, these contributing forces all add up to yield a single net force vector. This net force vector, then, gets mapped into its corresponding result vector. The result vector exists in another hypothetical space called "result space".
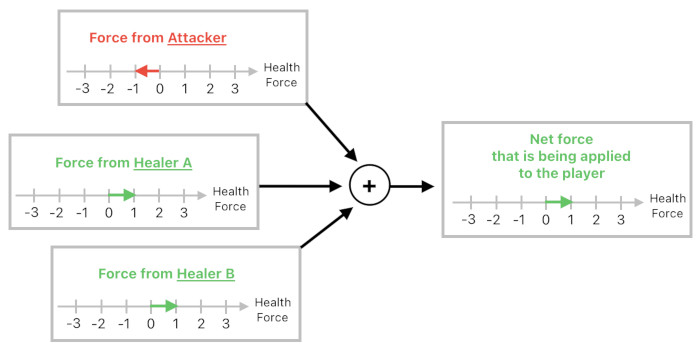
In the case of the player's health-changing event, we should consider the force space as the spectrum of all health-changing force values. So if the force is 0, you are doing nothing to the player's health. If the force is 1, you are increasing the player's health with the strength of 1 (This is what "healing" does). If the force is -1, you are decreasing the player's health with the strength of 1 (This is what "attacking" does). And so on.
The attacker applies the health-changing force of -1 to the player, while each of the two healers applies the health-changing force of 1 to the player. The net force is (-1) + 1 + 1 = 1, so we will conclude that the overall health-changing force that the player receives must be 1.
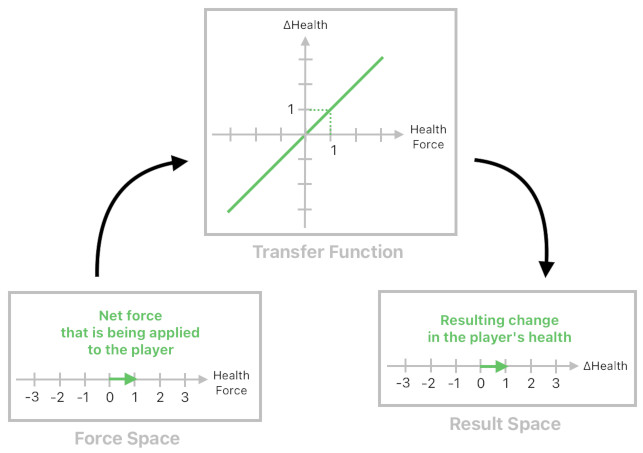
The health-changing event system, then, should be expected to take this net force vector (= 1) and transform it into its corresponding result vector which characterizes the change in the player's health (aka "ΔHealth"). Mathematically, such a process of transformation can be carried out by plugging the net force vector (as the input parameter) into the function called "transfer function", which basically shows us the one-to-one correspondence between force vectors and their result vectors.
Once the transformation part is complete, the only task remaining is to add the result vector (ΔHealth) to the player's current health. This is essentially what the player's health-changing event does whenever it executes itself.
But of course, one might be confused and say, "Dude, why do you overthink it? Just keep it simple. Simple is best. All you need to do is increase the player's health by 1 whenever a healer heals, and decrease it by 1 whenever an attacker attacks. You don't need such a fancy framework to do that!"
I am pretty sure that this is the exact kind of response which will be asserted a thousand times by a group of parrots unless I come up with a slightly more advanced example to show you the complexity of the issue. So here is an additional example.
Suppose that there is also a wizard who is casting a spell on the player. This spell is called "heal-blocker spell", and while it is affecting the player, it prevents him from being healed. How shall we implement this this?
A naive approach is to put a conditional statement inside the the gameplay logic, such as: "IF (the player is being affected by a heal-blocker spell), THEN (do not heal the player)". This might be a decent solution for small games. If the game happens to involve a hundred (or even more) types of spells, however, a decent developer will agree that hard-coding their effects using a bunch of conditional statements is not an okay way to do it.
A much more scalable way of implementing a spell (aka "status condition") is to define it as a modifier of an event's transfer function.
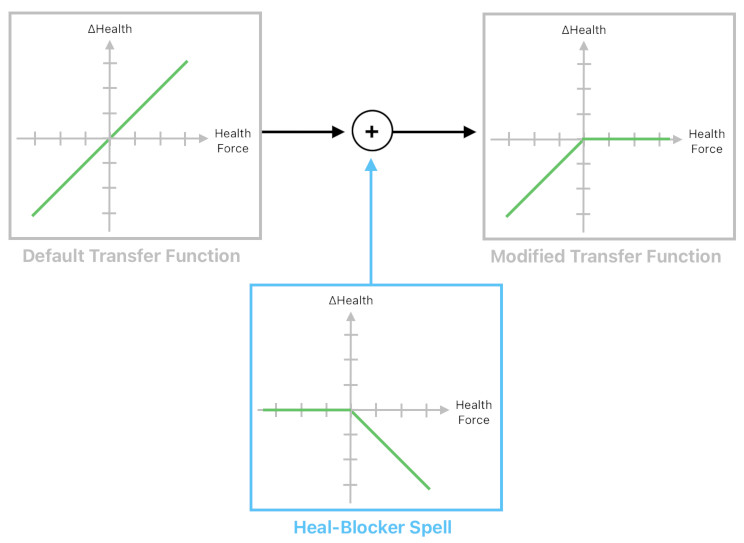
The default transfer function of the player's health-changing event is the identity function ("f(x) = x"). It gracefully handles both the force of heal and the force of attack because, whenever the force is a positive number (heal), the health will change in the positive direction with the rate that is proportional to the magnitude of the force, and whenever the force is a negative number (damage), the health will change in the negative direction with the rate that is proportional to the magnitude of the force. This is exactly what we would expect the health-changing event to do every time it receives a force.
When the player is under the influence of the health-blocker spell, however, such a transfer function is no longer valid because the player shouldn't be healed when he receives a healing force. Therefore, we must zero out the right half of the transfer function to enforce such a condition. And how do we do that? There are multiple ways, but the easiest one is to "add" another function to the transfer function which, after the addition, will cancel out the healing behavior of the original transfer function.
This additive approach is quite elegant because it is incredibly easy to undo the process of addition. Whenever we add the spell, we simply add the spell's modifier function to the player's current transfer function. Whenever we remove the spell, we simply remove (subtract) the spell's modifier function from the player's current transfer function. Since subtraction is the exact inverse of addition, no information will be lost and all the external factors (i.e. anything that is not part of the spell) will be preserved no matter how many times we add/remove the spell to/from the player.
Another application of the two-vector event model can be found in success-or-fail (aka "binary") scenarios, such as trying to let the character jump up a steep hill in order to proceed to the next stage. Imagine that there is a hill right in front of the player, and that the player is trying to reach the top of the hill by jumping. The player's current altitude is 0, and it will be shifted up to 1 once he successfully reaches the top.
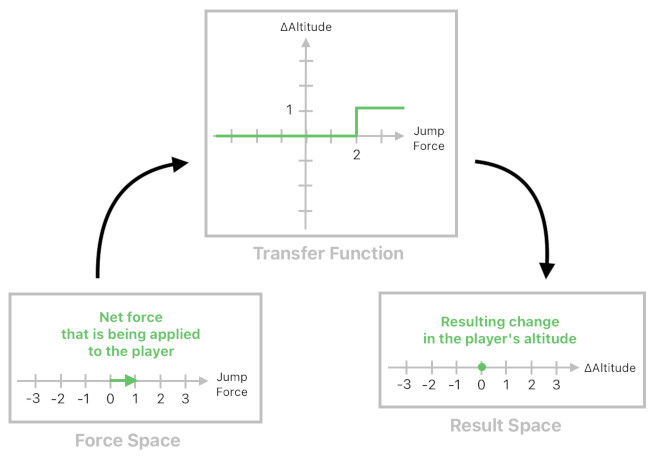
Just like we did in the previous example, we can use the two-vector event model for the problem of jumping. Unlike in the case of attacking and healing, though, we will now begin to assume that the force space refers to the range of "jump forces" (where high magnitudes denote powerful jumps and low magnitudes denote weak jumps), and that the result space refers to the change in the player's altitude after the jump.
The jump event has its own transfer function which is not an expression of proportionality between two variables, but a "threshold condition" which tells us how strong the player's jump must be in order to let him reach the top of the hill. In this example, at least the force of magnitude 2 is required to accomplish such a goal.
The main benefit of threshold-oriented gameplay scenarios (where you either CAN or CANNOT do something, not somewhere in between) is that it allows you to impose upon the player a specific set of keys which must be utilized in order to unlock his/her way out of the obstacle. If the hill were a smooth surface, for example, the player would've been able to climb it up by paying just a bit more effort and time. Under a strict yes-or-no condition, on the other hand (e.g. locked door, unreachable height, uncrossable river), it becomes possible to force the player to follow an absolute requirement such as: "You MUST have this item in your inventory in order to finish this task". This prevents the player from completing the whole game based solely upon brute-force and enough patience.
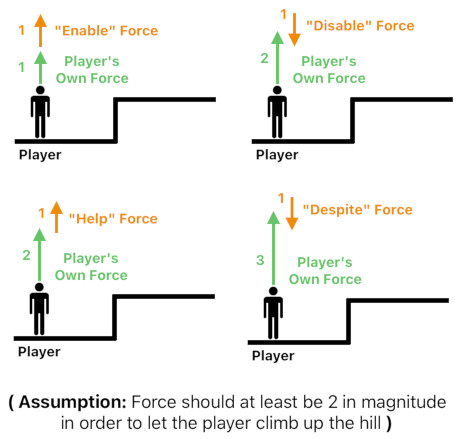
In his article on force dynamics (See "Event structure, force dynamics and verb semantics"), Gärdenfors shows us that an event's force vector can be classified into one of the following categories under the presence of a goal - "Enable", "Help", "Prevent", and "Despite". The "Enable" force, when added to the patient's current force vector, allows him/her to achieve the desired result which was unachievable before. The "Help" force is similar to the "Enable" force, except that its presence is not absolutely necessary because the patient is already able to achieve the desired result (with just a bit of additional time and effort). The "Prevent" force is the opposite of the "Enable" force because it disables the patient from achieving the goal which would have been achievable otherwise, and the "Despite" force is the opposite of the "Help" force.
Such categorization of forces is definitely feasible in a threshold-based scenario, such as the problem of jumping to reach the top of the steep hill. For example, if the player's initial jump force is only 1 and there is a "booster" item in the inventory which he/she can consume in order to add an extra boost of 1 to the jump force (which will achieve enough level of force to reach the top of the hill), we will be able to tell that this item is the "enabler" of the player's hill-mounting event. This way, we are able to sort various items, abilities, spells, and other numerous in-game factors into the four major categories (i.e. Enable, Help, Prevent, and Despite) and implement them appropriately based on how their presence will affect the progression of the game in binary (i.e. threshold-driven) gameplay scenarios.
Many of you who have implemented large-scale gameplay systems may have heard of the term, "data-driven". It is one of the most popular design philosophies in game development, in which the game's rules are specified in the form of declarative statements (e.g. data tables, English sentences, block diagrams, etc) instead of being hard-coded as part of the game's script itself.
Gärdenfors' event model nicely fits the spirit of data-driven gameplay design, due to the fact that it allows us to fully describe an event and its causal relation in the form of a plain English sentence (i.e. a declarative statement), instead of a bunch of conditional and iterative statements which are intertwined with one another (See "Causal Reasoning and Event Cognition as Evolutionary Determinants of Language Structure"). Engineers who have studied a logic programming language (e.g. Prolog) will instantly grasp the beauty of this, as well as how neatly it is going to mitigate many of the design complexities which tend to arise in gameplay engineering.
As long as we manage to express gameplay events as English sentences, we will be able to summarize all gameplay rules simply as a list of sentences and hardly anything else.
The examples I have shown so far are only one-dimensional - that is, each force space or result space is only a single number line, made up of a single variable (e.g. "change in health", "change in altitude", etc). However, this is just for the ease of visualization (because it is easier to draw 1D and 2D graphs than ones which are 3D, 4D, etc). In general, each force space or result space should be allowed to possess any number of dimensions, which may be spatial (x, y, z), temporal (t), or qualitative (e.g. color, temperature, health, mana, dexterity, experience, anger, happiness, attack strength, defense strength, and so forth).
Designing a transfer function which maps a multidimensional force vector to a multidimensional result vector is indeed a difficult thing to do. If you consider each vector as just an array of numbers (e.g. "int[]"), however, you will be able to tell that the two-vector event model is nothing more than a "list-mapping process" - a generic system which takes a list of numbers as the input, and generates another list of numbers as the output. One of the easiest ways of designing such a system is to treat each element of the output list as a linear combination of the elements of the input list. This lets the system's transfer function be constructed as a simple matrix multiplication, which is something your graphics card (GPU) can do extremely well.
I would really like to thank Katarina Gyllenbäck for introducing the works of Professor Gärdenfors. I would have not had a chance to delve into his profound insights in the field of cognitive science, if she did not introduce his papers in her articles.
Katarina Gyllenbäck, who is both a narrative designer and a researcher of interactive media, has shown me a narrative-driven interpretation of Gärdenfors' two-vector event model. It is most thoroughly illustrated in her description of conceptual space in the article, "Part 11, The Meaning-Maker's Space".
To learn more about her areas of insight, please visit Here to see my review of her writings on narrative design. Or, you may want to visit her website and read her vast collection of articles Here.
1. Event structure, force dynamics and verb semantics by Peter Gärdenfors (This article most accurately summarizes the mathematical pattern behind the causal relations of the two-vector event model.)
2. Causal Reasoning and Event Cognition as Evolutionary Determinants of Language Structure by Peter Gärdenfors (This one most thoroughly describes the linguistic interpretation of the two-vector event model, explaining why an event can be considered a sentence and each element of the event can be considered a phrase such as a "noun phrase", "verb phrase", etc)
3. Primary Cognitive Categories Are Determined by Their Invariances by Peter Gärdenfors (This is a great introductory text to the idea of "Conceptual Space" - a hypothetical space which expresses the qualitative attributes of an object as a point in geometry. It also explains how a set of invariances in our domain of cognition (i.e. a dense cluster of sense-data) eventually manifest themselves in the form of a discrete entity called "object". This is one of the most foundational ideas in the study of artificial intelligence and machine learning (often referred to as "pattern recognition").)
4. Events and Causal Mappings Modeled in Conceptual Spaces by Peter Gärdenfors (This is a general overview of how the force and result vectors are related to one another in an event. In this paper, Professor Gärdenfors tells us various subleties that are involved in the dynamics of causality, such as the capacity of the human mind to perform interpolation between two force vectors (which means that the total domain of forces which can be formed by a set of basis force vectors is their convex hull), etc.)
5. From Sensations to Concepts: a Proposal for Two Learning Processes by Peter Gärdenfors (This article introduces some of the experimental results which show us that, during early childhood development, young children do manage to learn how much an object (i.e. a cluster of data points) differs from another object (i.e. another cluster of data points), but not necessarily the direction (i.e. dimension) in which they differ. It is only later stages in life during which they acquire the ability to break down each object as a product of multiple dimensions and make comparisons based upon individual dimensions, not only in terms of the overall distance between two clusters of data).
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service