
Author: Youngjin Kang Date: November 30, 2025
This article is Part 27 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
In the previous article, we looked at various methods of representing relations within a one-dimensional table. The main takeaway was to simply format each relation as an object which contains a pair of references. So far, so good.
The issue, though, is that we haven't figured out yet how to update (modify) such relations for gameplay purposes.
For obvious reasons, a game is a dynamic system which must be able to make changes to its own state as time passes by. If nothing changes no matter how much the player interacts, there won't be any reason to "play" such a game.
Even the most idle-looking game, such as one which only involves a single player whose mission is to escape a completely static maze, still requires some kind of modifiable state (because the player's position is part of the state and it changes over time).
Therefore, it is important for us to find out how to modify a relation's state, so as to leverage it as part of game mechanics.
Let us begin with a super simple example. Suppose that the player has 3 energy points. What shall we do to express this in our data table?
As you may remember from the last article, it is advisable to model everything as an object with 2 reference slots. In our case, the player is an object, and he is associated with a relation which tells us how many energy points he has. This relation, too, is an object with 2 reference slots.
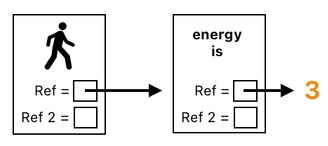
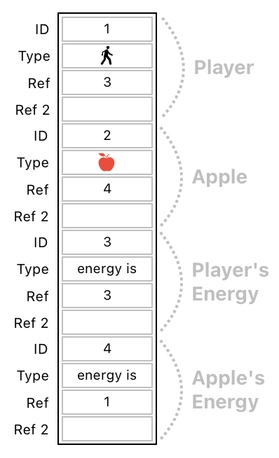
In table form, each of these objects can be written down as a sequence of 4 data entries.
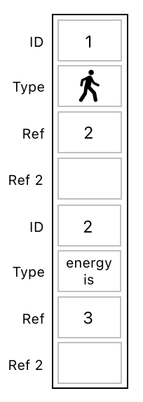
Nothing new has been introduced so far; we already know how to format a relation inside a table. So, here comes something which hasn't yet been dealt with.
Let us say, for instance, that he player's energy is supposed to diminish over time. This makes sense, doesn't it? Since the player is a biological being, he must keep spending his energy to stay alive.
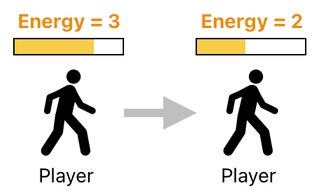
Here is how the nature of such gradual decay can be simulated. Let us assume that, after a bit of time delay, the player's energy decreased from 3 to 2. This will correspond to a change of value in the 7th data entry (See the table below).
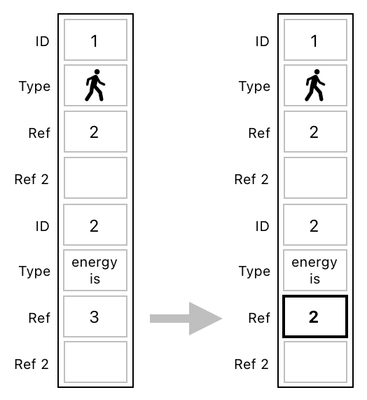
The way we can execute such a transformation is relatively straightforward, as long as we know the nature of linear algebra. First off, let us attach an extra "1" at the very bottom of the table. This number represents the rate of the player's energy consumption.
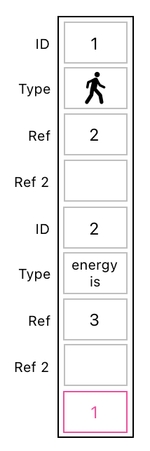
Next, let us multiply this table by a matrix which copies the value of the table's last slot (which is 1) and subtracts it from the slot which contains the player's energy.
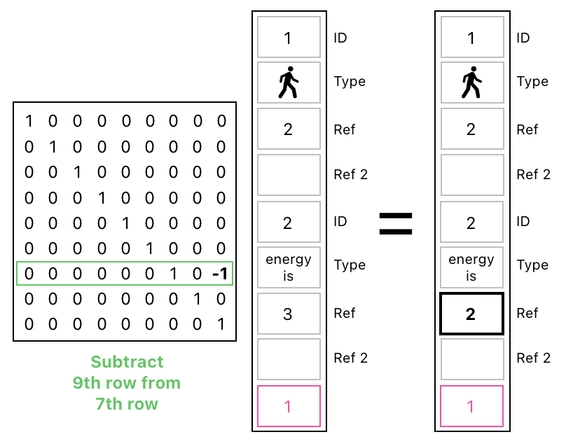
And, boom! Here it goes. You can clearly see that this matrix multiplication just made the "energy is" relation point to number 2 instead of number 3. The player now has 2 energy points.
Here is a slightly more complex example. Suppose that the player absorbed 1 energy point from the apple by eating it (See the picture below).
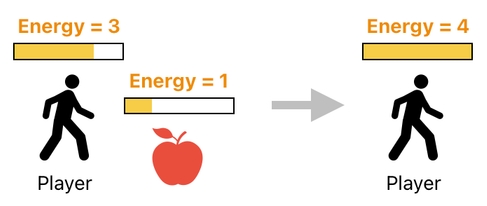
What shall we do to make this happen in our data table?
In terms of objects and references, such a transformation can be depicted as shown below. The apple and its energy-specifying relation will simply disappear, and the apple's energy will be added to the player's energy.
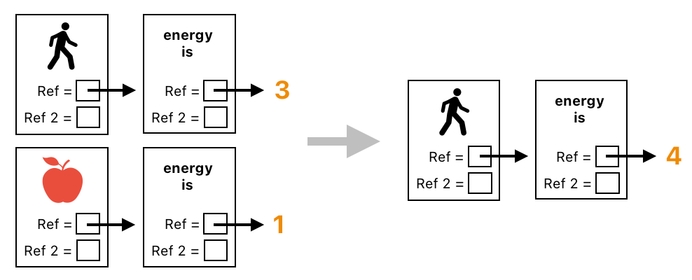
What about in table form? First of all, let us draw out our initial state as a one-dimensional data table, where both the player and the apple, as well as their respective relations, are gathered as parts of a single column.
The transformation we desire in this model consists of a few simple modifications. First, we want the player's energy to change from 3 to 4, which can be done by simply modifying the 1st reference value of the player's relation from 3 to 4. Meanwhile, we also want to clear out the portions of the table which correspond to the apple and its relation.
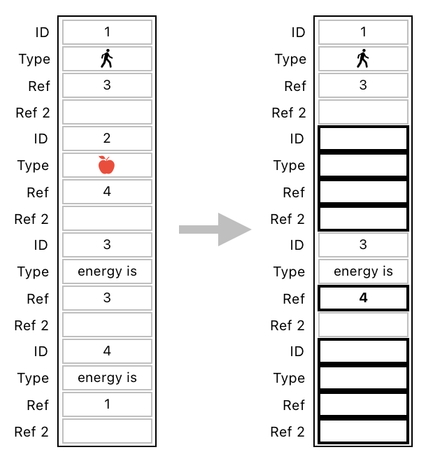
And the good news is that a single matrix multiplication will suffice in making such a set of changes. Take a look at the matrix shown below, which is responsible for simuntaneously carrying out 3 separate actions - (1) Adding the apple's energy to the player's energy, (2) Erasing the apple, and (3) Erasing the apple's energy.
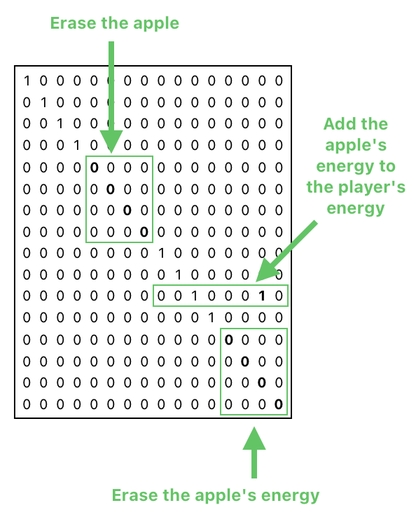
This is an example of a "transaction matrix", since it executes a transaction of multiple events. When you take the product between this matrix and our data table (as shown below), you will see that it yields the desired result.
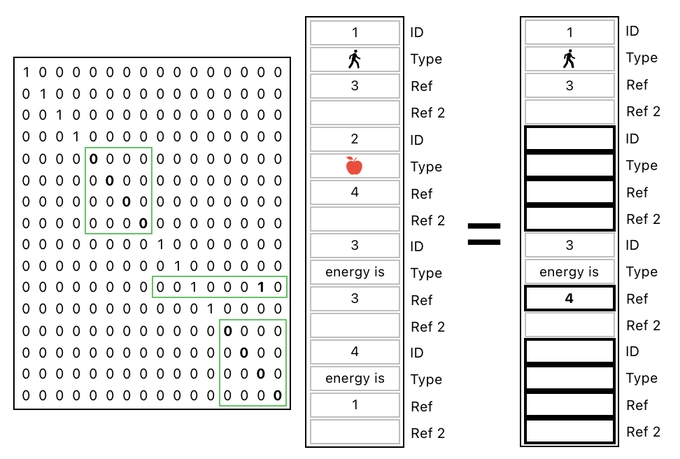
So, here we have it. We just proved that it is possible to manipulate multiple relations at once, for the sake of simulating innumerable kinds of gameplay interactions.
Some interactions, though, are not supposed to be black-and-white in nature.
As you may have noticed, our previous example was quite black-and-white in the sense that the player just swallowed the entire apple all at once. This simplified the problem immensely; all we had to do was completely wipe the apple out of existence and add its energy to the player.
A more realistic scenario, on the other hand, would rather be grayscale in nature; that is, it would let the player spend some time taking bites out of the apple instead just swallowing it instantly.
Here, I will show you yet another example for demonstration purposes. Imagine that the player's initial energy is 1 and the apple's initial energy is 3.
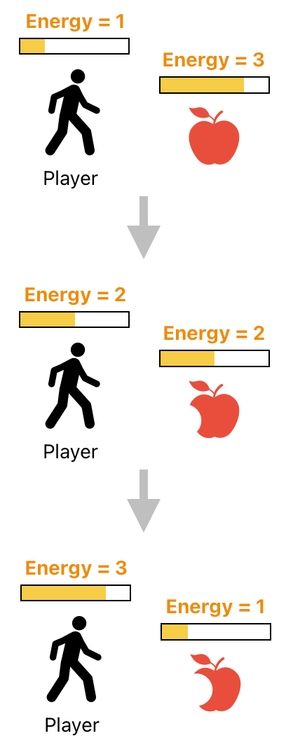
During the first step in time, the player absorbs 1 energy point from the apple by taking a bite of it, thereby increasing his energy level by 1 and decreasing the apple's energy level by 1. And during the second step in time, the player once again absorbs 1 energy point from the apple by taking a bite of it, thereby increasing his energy level by 1 and decreasing the apple's energy level by 1. And so on.
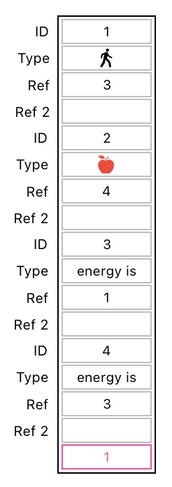
If we express the first step in the language of relations, we will see something like this:
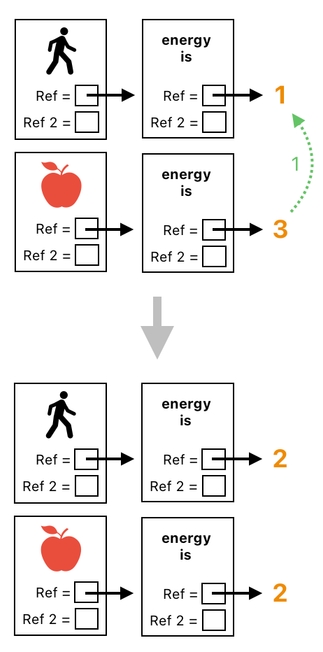
In table form, such a transformation will be expressed in the following way:
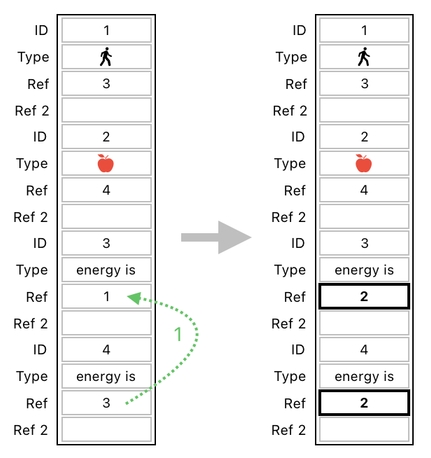
As you can see, all we are doing here is simply add 1 to a data entry and subtract 1 from another data entry.
One major difference here, in comparison with our previous example, is that we are not transferring ALL of the apple's energy to the player in this case; instead, we are just transferring a small portion of it (i.e. 1 out of 3 energy points).
And the way we execute a transaction like this, once again, will only require a single matrix multiplication; only in this case we will need to do some additional tweak beforehand, since our aim is to change the energy levels by some fixed amount here. First, let us attach an additional "1" at the bottom of our table.
This new element will serve as the "rate of energy transfer" in our scenario.
With this extra piece of data, we are now able to construct our transaction matrix which, when applied to our data table, will increment the player's energy by 1 and decrement the apple's energy by 1. It is shown below.
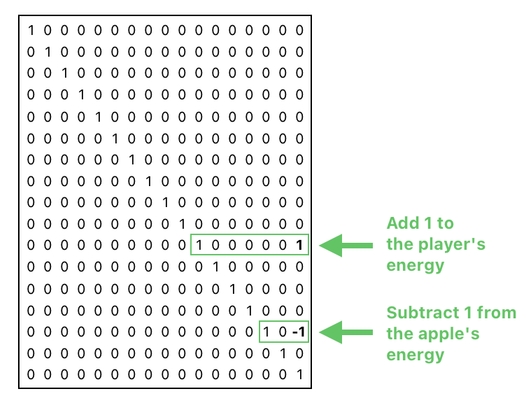
As it is clearly denoted, this matrix comprises two actions - one which increments the player's energy by adding the table's last element to it, and the other one which decrements the apple's energy by subtracting the table's last element from it.
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service