
Author: Youngjin Kang Date: November 27, 2025
This article is Part 26 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
Okay, so we just saw the merits of handling data in one dimension.
We should remind ourselves, though, that we have barely scratched the surface of what we are going to see next.
Note that, in Part 23 and Part 24 of this series, I introduced the concept of relations as some of the most fundamental building blocks of gameplay. The thing is that, while describing the nature of relations, I never explaind a way to manipulate their states using linear algebra.
Such omission was chiefly due to practical reasons. A two-dimensional table, composed of both rows and columns, is not so straightforward a model to handle relations by means of matrix multiplications. A one-dimensional (i.e. single-column) table fits such an objective more elegantly.
Before learning how to use relations for gameplay purposes, therefore, we must first learn how to represent them one-dimensionally.
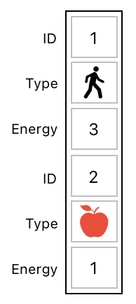
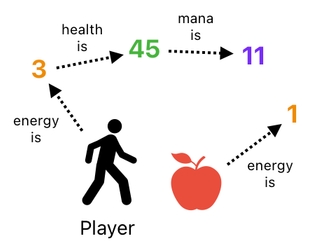
Let us revisit our previous example in which there are two objects - the player and the apple. The player's energy level is 3, and the apple's energy level is 1. They are both listed inside a single column.
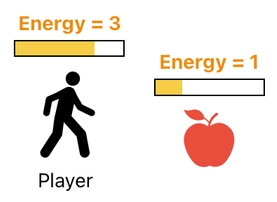
A more pictorially enriched depiction of this scenario is shown below. Here, I am representing each energy level as a bar.
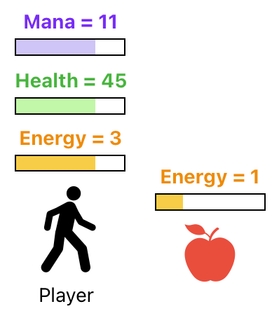
While designing a video game, however, we often feel the necessity to add more types of numbers (i.e. state variables) to a game character. For instance, we may want the player to be equipped with not only energy, but also health and mana.
Perhaps the most direct way of implementing these in our data table is to let each object have 2 additional slots - one for "health" and the other one for "mana".
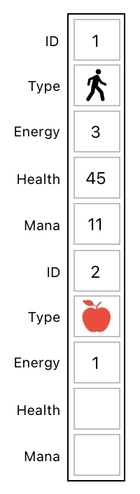
This, of course, is not a scalable solution at all. Imagine that we decided to let the player have hundreds of numbers associated with him, while still requiring the apple to possess just a single number called "energy". This will force the apple's section of the table to carry hundreds of empty slots just to fill the gap.
Fortunately, this kind of scaling issue can be avoided by using relations, such as the ones shown here:
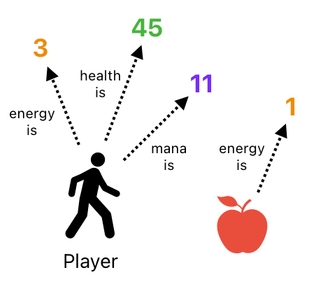
Here, we have a bunch of relations that are responsible for denoting the characteristics of both the player and apple. The "energy is" relation denotes the player's energy, for example.
If we represent every one of these relations as an object, it will look something like this:
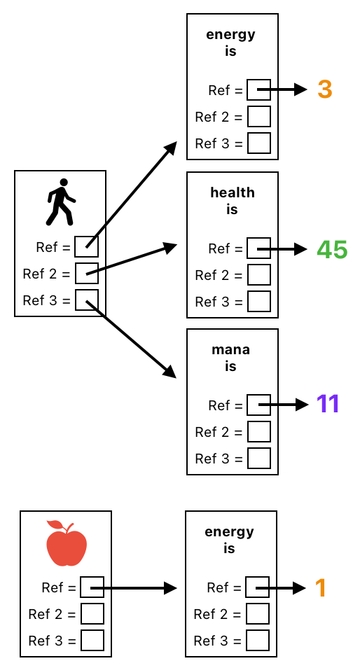
Each object contains 3 reference slots, implying the capacity to point up to 3 other objects. As you can see, the player is pointing the 3 relations which describe his energy, health, and mana respectively. The apple, on the other hand, is pointing a single relation which describes its energy.
This looks neat. But again, we ought to be aware of the problem of scalability. If we are to convert the above diagram into a one-dimensional table, we will have to come up with a quite undesirably long list of values, which begins like this:
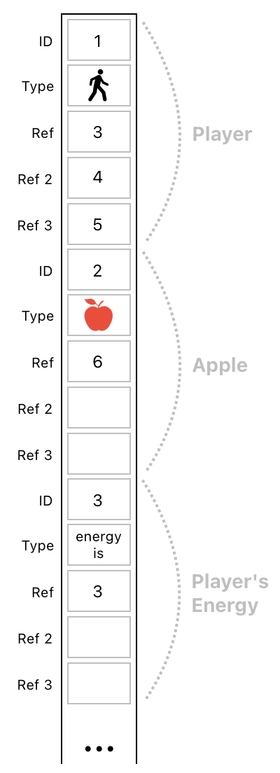
... and continues all the way down to:
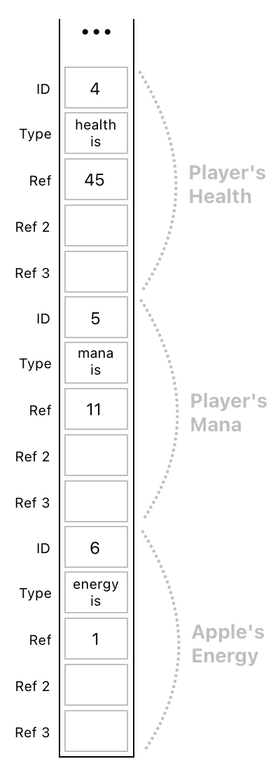
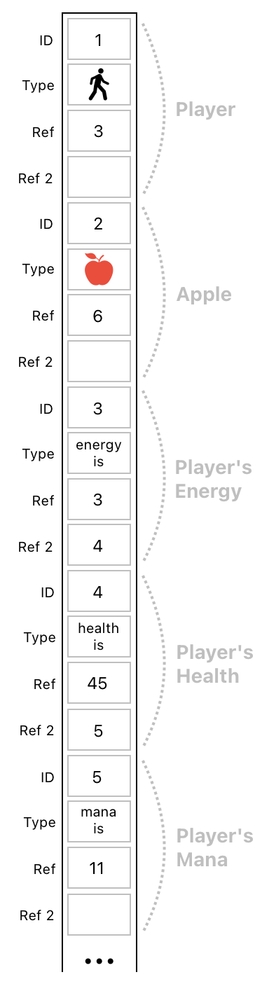
In this table, every object consists of 5 data entries (1 for ID + 1 for Type + 3 for references). Since every relation is an object and there are 4 of them (aside from the player and apple), we need 6x5 = 30 entries in our data table.
This does not seem too much in our particular scenario. If we want each object to be able to bear an enormous number of properties, however, a great deal of wasted space will emerge.
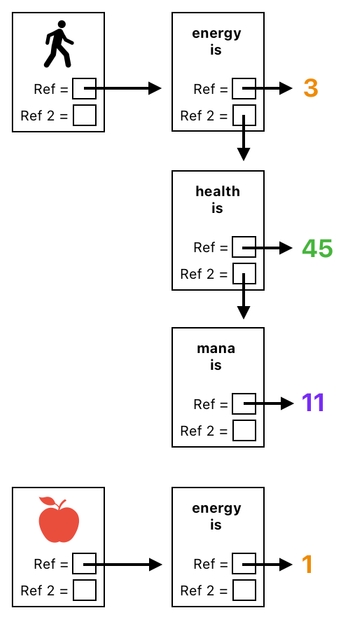
So, here is a better solution, Why don't we just tie up the player's relations as a single chain (as illustrated in the picture below)?
If we do it this way, we will be able to get away with just up to 2 references per relation. Inside each relation, the first reference will hold the value (e.g. energy, health, etc), while the second reference will be pointing the "next" relation in the chain.
In table form, it can be written like the one shown below.
Oh, but not every property can be represented as a single number. Some of them, such as position, velocity, and other multidimensional species of information, must be expressed in terms of vector quantities. For example, we might wish to record the player's current position as a 2D vector (a pair of numbers). How shall we implement that?
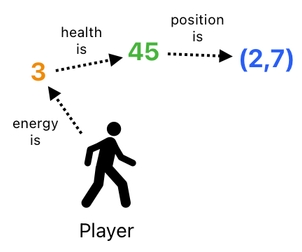
Okay, it is not that difficult. All we have to do is leverage a relation's first and second references as the two spatial coordinates (X and Y). Such a relation may be referred to as a "pair of" relation, since it relates a pair of numbers (X and Y) to the player's position.
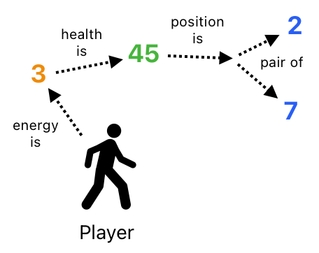
In terms of objects, it can be structured as the following:
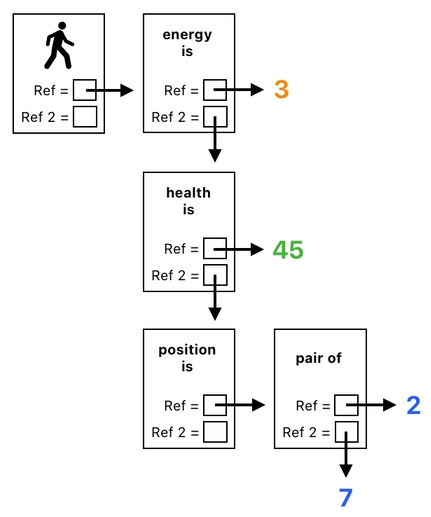
There is yet another limit to the aforementioned solution, though. What if the player is associated with not just a single 2D vector, but multiple 2D vectors? For example, we could easily imagine a scenario in which we need to keep track of the player's velocity besides position.
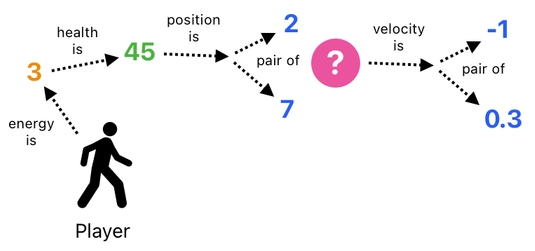
In case we encounter a situation like this, we will be unable to group all of the player's properties as a single chain of relations unless we let each object carry more than 2 references. So, shall we assign 3 references to each object instead of 2?
But wait - hold on. We've got a much better way of handling this level of complexity.
Here is a hint. Relations can come in multiple layers; that is, a relation can refer to other relations, which in turn can refer to yet another group of relations, and so on. It may as well be stated that there could be "relations about relations".
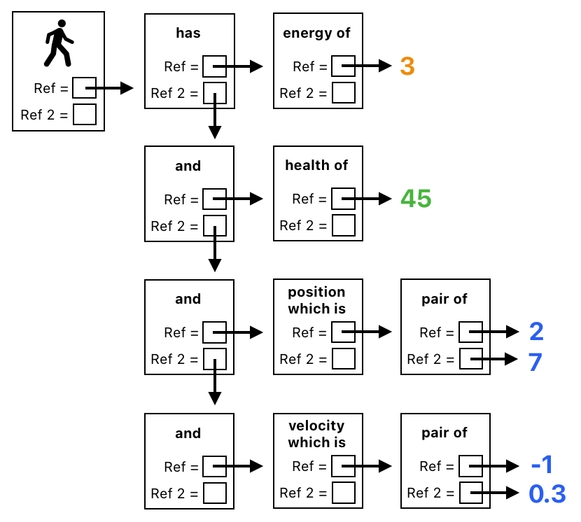
This sounds confusing, so I will give you a concrete example to clarify things a bit. First off, if we express the above diagram as a single English sentence, it will be written like this:
The player has the energy of 3, the health of 45, the position which is a pair of (2, 7), and velocity which is a pair of (-1, 0.3).Here, we are seeing different types of relations. Some of them simply describe properties that the player happens to possess (such as "energy of", "health of", "position which is", etc), while others play the role of joining such elementary relations with one another (such "has" and "and").
Pictorially, the sentence written above can be structured in the following manner:
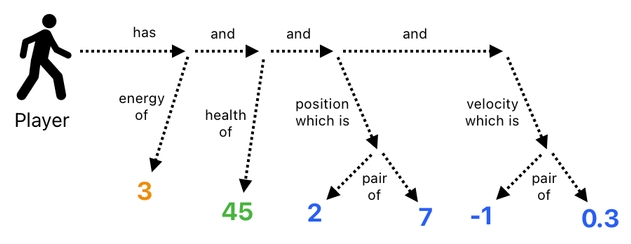
The player still carries a chain of relation, which goes like: [has -> and -> and -> and]. However, the chain itself branches out into more specific relations, some of which further branch themselves out to be able to hold multidimensional data (such as a pair of numbers).
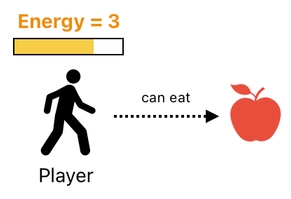
By letting relations refer to other relations, we are able to express pretty much any gameplay scenario without complicating things too much. For instance, imagine a case in which the player has 3 energy points and is able to eat the apple.
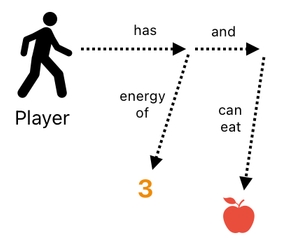
This can be broken down to 4 relations in total - 2 for describing the player's characteristics (i.e. "how much energy he has", "what he can eat", etc), and the other 2 for binding these two relations to the player by means of conjunctions (e.g. the word "and").
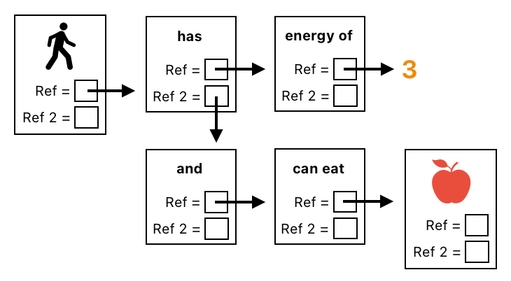
And this, of course, translates to:
Okay, here comes a more intellectually challenging example. Let's say that the player likes the fact that he can eat the apple. How shall we formulate this kind of situation in terms of relations?
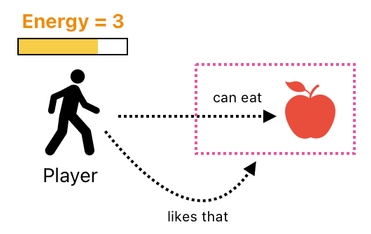
Again, we should remind ourselves that a relation is capable of referencing another relation. So, all we need to do is simply let the player's "likes" relation point to the "can eat" relation.
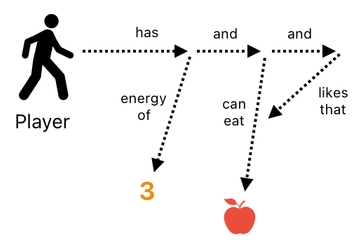
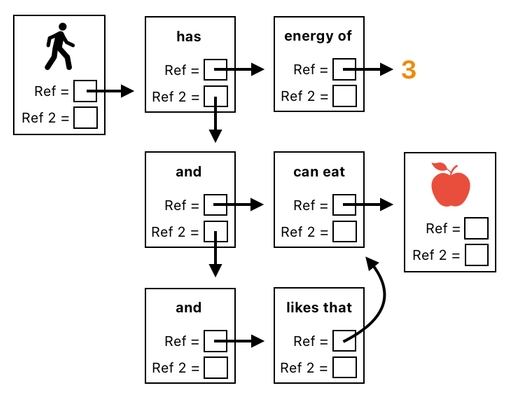
A plain English expression of this would be:
The player has the energy of 3, can eat the apple, and likes the fact that he can eat the apple.
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service