
Author: Youngjin Kang Date: November 22, 2025
This article is Part 25 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
So far, we have been modeling our game world as a table which consists of rows and columns. From a structural point of view, such a table can be described as a two-dimensional grid.
Across the vertical direction, we have a list of rows. Across the horizontal direction, we have a list of columns. Each row is a "thing" inside the universe, whereas each of its column values is a property that the thing happens to possess.

Such a representation is fairly intuitive, and it is perhaps the most popular method of presenting data throughout the industry.
Everywhere, we see people using spreadsheets to keep track of revenue and expenses, customer records, shopping lists, and countless other types of data for business needs. Such sheets are made of rows and columns, just like the ones we have been seeing in our gameplay examples.
We have also encounterd the bitter truth, however, that a two-dimensional table often turns out to be a pain to deal with when it comes to matrix multiplication.
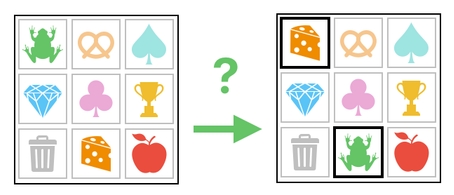
Since a matrix multiplication is unable to modify just a portion of each row/column, the process involved in fiddling with individual data entries requires so many steps and is therefore too complex.
Fortunately, we have a way to circumvent this problem entirely.
The idea is that, if we keep ALL our data in just a single column (or row), we will no longer be facing the problem of having to go through a series of complicated steps (such as spliting the table into parts and rejoining them later on, etc) just to change one of the data entries.
How? Here, let me show you. First off, please have a look at the example shown below.
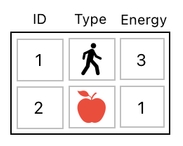
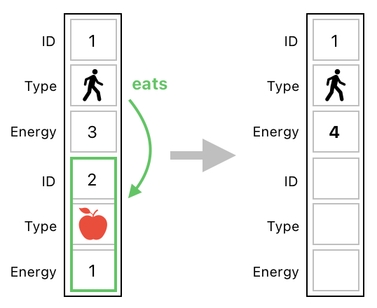
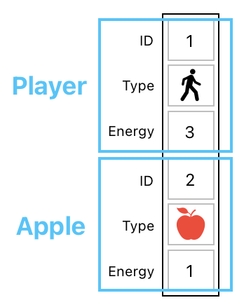
This table tells us that there are 2 objects in the game world - the player (denoted by a human figure) and the apple (denoted by a red apple icon). The amount of energy stored in the player's body is 3, and the amount of energy stored in the apple is 1.
Let us imagine that the player decided to eat the apple in order to absorb its energy. The following image shows us what happens when such a decision gets carried out; the apple's data (row) will be erased due to its destruction, and its energy will be added to the player's energy.
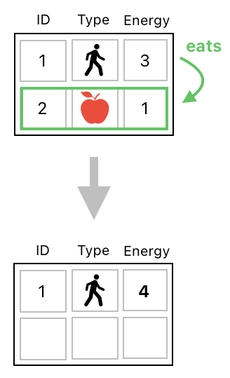
If we are to apply such changes to our table by means of linear operations such as matrix multiplication/addition, we will surely face a hard time. Erasing the apple's row is not difficult at all; the real challenge lies on the act of selectively manipulating one of the column values (i.e. energy) without tampering with the other columns, which is something we cannot accomplish with a single matrix multiplication.
The way we can prevent this sort of concern entirely, is to "flatten out" our data table so that there will be only one column left. The following image shows the result of such a flattening process.
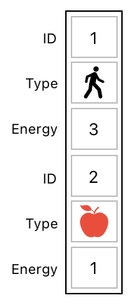
As you can see, both of the table's rows turned into columns (i.e. rotated by 90 degrees), and then joined themselves to yield a single column. In this new table, the first 3 rows represent the player and the last 3 rows represent the apple.
Now, let's say that the player decided to eat the apple. What shall we do to make that happen?
Again, we want the apple to be destroyed (because nothing can exist after being eaten), and the player's energy to be incremented by the amount of energy stored in the apple.
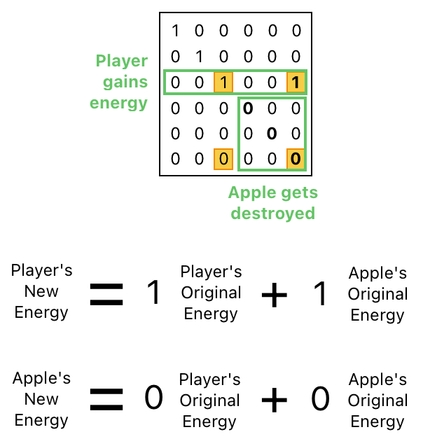
The good news is that, now that everything is in one column, we can do pretty much anything by means of a single matrix multiplication. Here, take a look at the following operation:
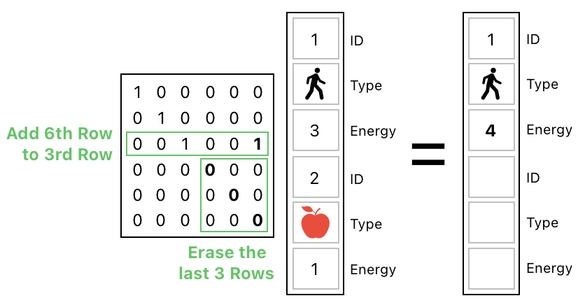
See? I just multiplied the table by a single matrix, and it swiftly achieved both of the goals I mentioned above. The extra "1" in the 3rd row of the matrix resulted in adding the apple's energy to the player's energy, and the zeroes in the last 3 rows of the matrix resulted in wiping the apple's data entries out of existence.
Aside from simplicity, this "flattening" methodology also makes it easy to accurately mirror the atomic nature of our gameplay events - "atomic" in the same sense that a transfer of money from one bank account to another is atomic.
Here is an example. When a guy sends money to someone else via a banking app, we expect 2 events to occur simultaneously:
(1) A decrease in the sender's account balance, and
(2) An increase in the recipient's account balance.
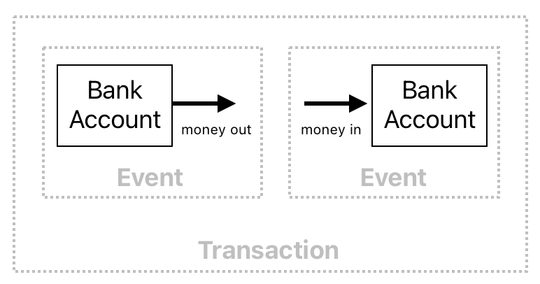
It will be disastrous if only either of these two events manage to take place. These 2 events must either both occur, or both fail to occur, meaning that they are always supposed to be grouped as a single, indivisible entity (hence the word "atomic"). We call such a group of events a "transaction".
The act of eating an apple can be considered a transaction, too, since it involves a group of events which must always happen simultaneously.
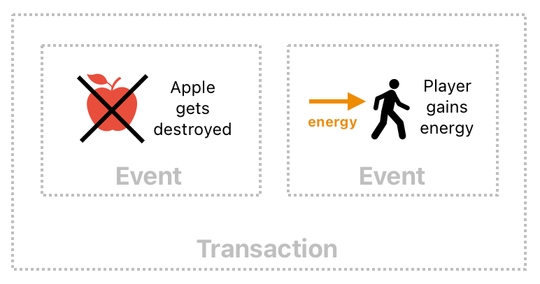
Eating an apple should increase the energy of the eater, while also destroying the apple that is being eaten. We cannot possibly let either one of them happen without letting the other one happen as well; these 2 events must always come together.
And what is so nice about our foregoing matrix implementation is that it lets us pack these 2 events in a single unit of operation. The matrix shown below, for instance, is responsible for incrementing the player's energy AND destroying the apple at the same time, whenever our data table is multiplied by it.
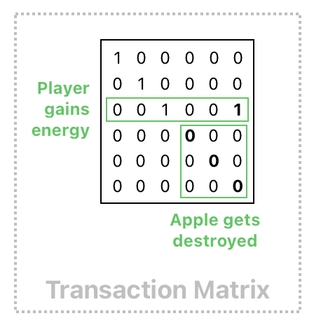
Such a kind of matrix can be stated as a "transaction matrix", since it includes the set of instructions needed to execute a transaction.
One downside of modeling the entire table as a single column (i.e. one-dimensional sequence of values rather than a two-dimensional grid) is that it makes it hard to see which properties are associated with which objects.
In a two-dimensional table, we are able to identify a single list of contiguous values in which properties of the same sort can be found. The table shown below, for example, clearly shows us that its 1st column contains its "ID" values, its 2nd column contains its "Type" values, and its 3rd column contains its "Energy" values.

In the one-dimensional (flattened) version of the table, on the other hand, we can no longer view properties of the same sort in a single list because they are scattered all over the place and are not adjacent to one another.

However, we can still recognize a pattern here which is pretty straightforward. Although properties of each kind are no longer grouped as a distinct column, they are still "grouped" in the sense that they are all separated by an equal distance.
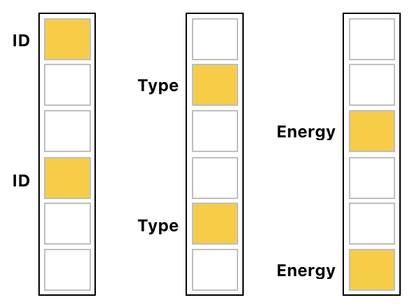
As you can see, "ID" values are 3 entries apart from each other, "Type" values are 3 entries apart from each other, and "Energy" values are 3 entries apart from each other.
The difference among these three categories (i.e. "ID", "Type", and "Energy") is the offset. Let me explain what I mean by this.
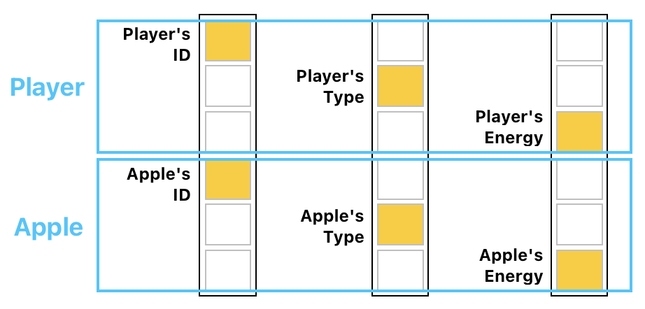
If you split the table into chunks of 3 elements, you will see that each chunk corresponds to an object (In our case, the first chunk is the player and the second chunk is the apple).
It is then obvious why the offset lets us identify the category of each element. The 1st element of each chunk (object) is its ID, the 2nd element is its Type, and the 3rd element is its Energy.
This kind of insight comes in handy when we are designing a transaction matrix. In the case of energy exchange, for instance, we know that the entries which are responsible for transferring the energy always reside in every 3rd row/column of each 3-by-3 block.
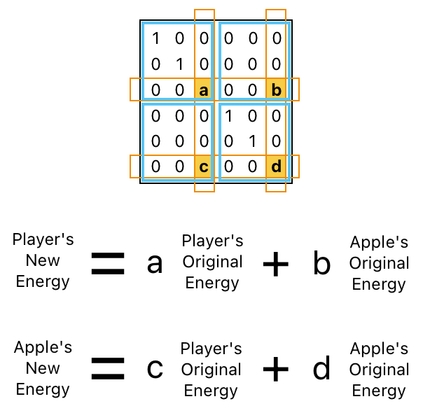
Such a piece of knowledge helps us decipher the anatomy of the matrix we saw before, in the example in which the player consumed the apple and gained energy from it.
 Previous Page
Next Page
Previous Page
Next Page

© 2019-2025 ThingsPool. All rights reserved.
Privacy Policy Terms of Service