
Author: Youngjin Kang Date: November 2, 2025
This article is Part 22 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
By now, you are probably familiar with how collision detection works. If you paid attention to the foregoing article, you must be able to use the technique I described to find out which objects are colliding with which.
So far, so good. But the problem is, we usually do not detect collisions just for the sake of collision itself; we also want to use it for practical purposes, such as triggering interactions between objects based on the manner in which they collide, and so on.
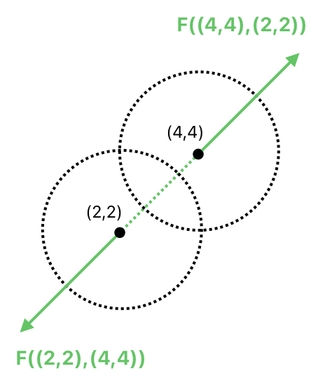
The most basic kind of interaction can be found in the context of physics. When pieces of matter (i.e. rigid bodies) bump into one another, for instance, they must push each other away. Such a phenomenon can be modeled in terms of a pair of force vectors, such as the ones shown here:
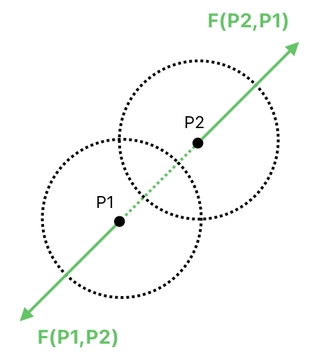
This figure tells us that there are two circles, whose center positions are P1 and P2, respectively. Since their areas overlap, we can say that they are colliding.
If we assume that both of them are rigid bodies (i.e. physical objects with mass and volume), there will have to be a pair of force vectors which are responsible for pushing these circles away from each other. "F(P1,P2)" is the force which pushes P1 away from P2, while "F(P2,P1)" is the force which pushes P2 away from P1.
As soon as the forces get applied, new values will be assigned to both P1 and P2. This will shift the positions of the two circles in way which ensures that their distance is greater than before.
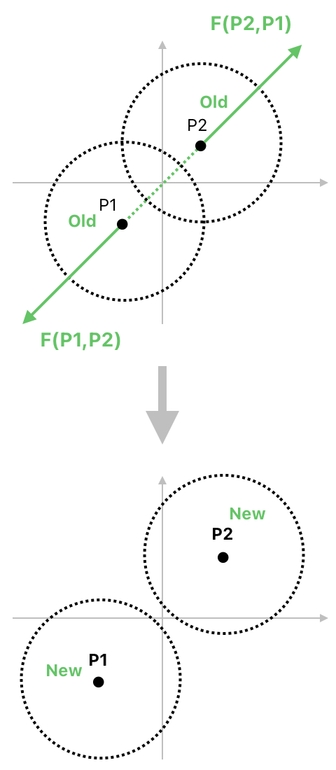
In a realistic context, it should make sense to imagine a force as an indicator of one's acceleration. For simplicity, however, let us just suppose here (in our fictional physics) that simply adding the force to the original position will give us the new position (i.e. the position after the force gets applied).
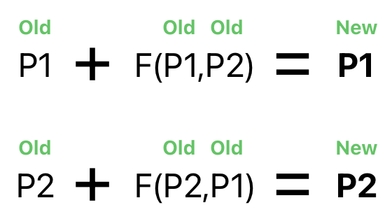
In order to integrate physics into our gameplay system, we need to do something more than just stating the relation between force and position; that is, we ought to come up with a way of actually computing the forces and applying them to their corresponding objects.
For this purpose, we must first begin by redefining our "C" function (i.e. collision detection rule) into something like this:
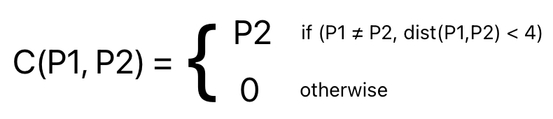
The expression above looks almost the same as the one I have shown you before, except that the "1" is now "P2" instead.
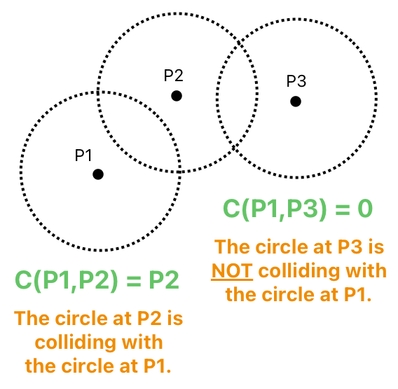
Whereas the "1" in the previous definition of "C" could only tell us whether a pair of circles are colliding or not ("1" for "colliding" and "0" for "NOT colliding"), our new "C" function now provides us with the information which answers the question: "What is the position of the circle (P2) that the given circle (P1) is colliding with?"
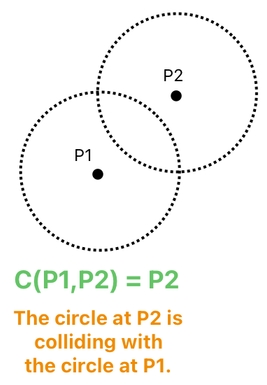
If the result of the function is 0, it means that there is no collision. If the result is something other than 0, on the other hand, it must be the position of the neighboring circle that the given circle (whose "position" is specified in the first argument of the "C" function) is currently colliding with.
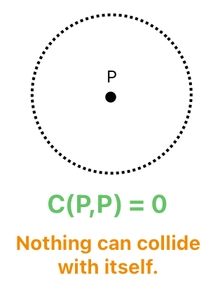
And of course, if the two circles are located at the same exact spot, we say that they are the same circle (assuming that it is impossible for multiple circles to coincide at the same exact spot). Since nothing can collide with itself, it can be asserted that "C(P,P) = 0", where "P" refers to any arbitrary point in space.
With this new version of the "C" function, we are now ready to compute physical forces which will ensue from the state of collision.
Recall that, in the previous article, we saw that the result of detecting collisions turned out to be a grid of 1s and 0s.
The reason behind this was that, in our previous definition of "C", the result was always supposed to be "1" whenever a collision occurred between a pair of circles and "0" otherwise. There was no information to tell us anything about the "other circle" with which the given circle was colliding.
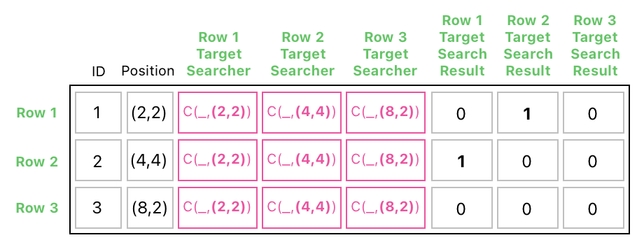
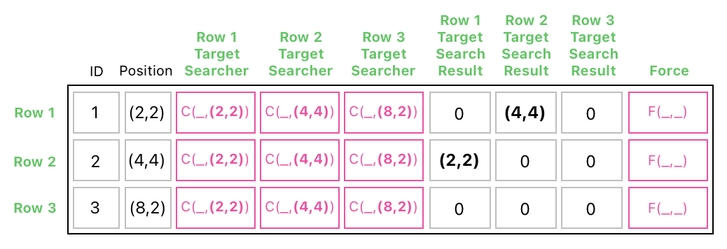
Now that we have redefined our "C" function, however, we are able to fill our search results with a richer set of data. Let us re-evaluate the instances of the "C" function, which are reproduced below.
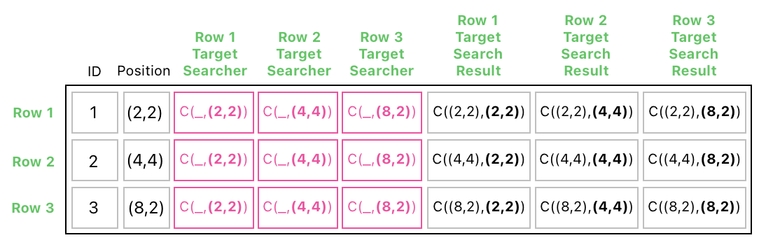
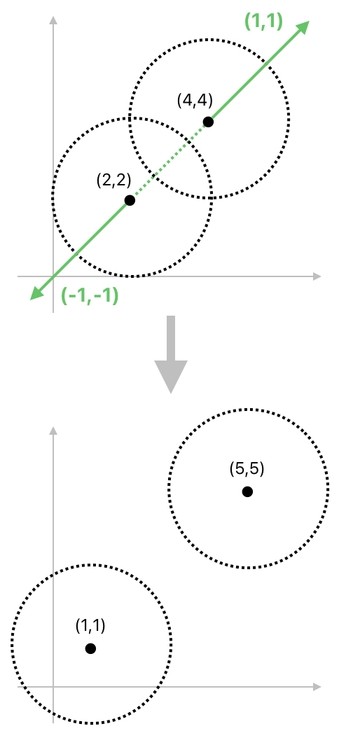
Okay! As you may remember from the previous example, only the circles at (2,2) and (4,4) are colliding with each other. So, we can still conclude that only "C((2,2),(4,4))" and "C((4,4),(2,2))" will result in nonzero values.
What is the value of "C((2,2),(4,4))"? By our new definition, it must be (4,4) because (2,2) and (4,4) are not identical and the distance between them is less than 4 (where 4 is the minimum distance required to ensure that the two circles do not overlap). For a similar reason, the value of "C((4,4),(2,2))" must be (2,2).
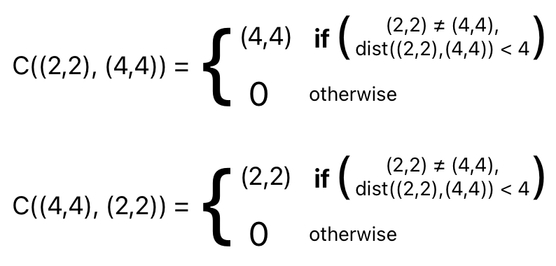
This eventually yields the following search result:
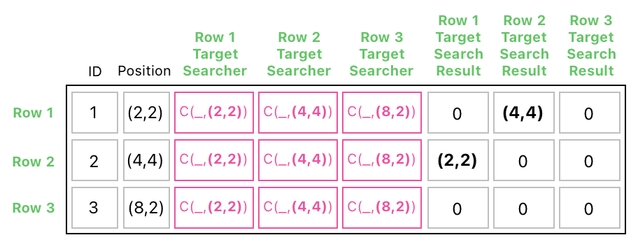
Instead of just 1, here we've got the origins of collsion - i.e. positions of those who are "pushing" their neighbors due to physical contact.
The 2nd element of "Row 1's Search Result" is set to (2,2). This indicates that the 2nd row's circle is being pushed away by the circle at (2,2).
Similarly, the 1st element of "Row 2's Search Result" is set to (4,4). This indicates that the 1st row's circle is being pushed away by the circle at (4,4).
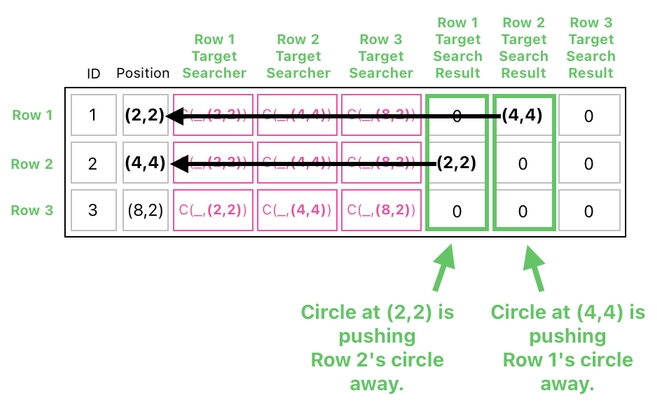
And by "push", I mean a force which is being applied from one circle to the other.
For example, a push that the circle at (4,4) receives from the circle at (2,2) can be written as "F((4,4),(2,2))", since the first argument of "F" denotes the force's recipient whereas the second argument denotes the force's sender (and vice versa for the circle at (2,2)).
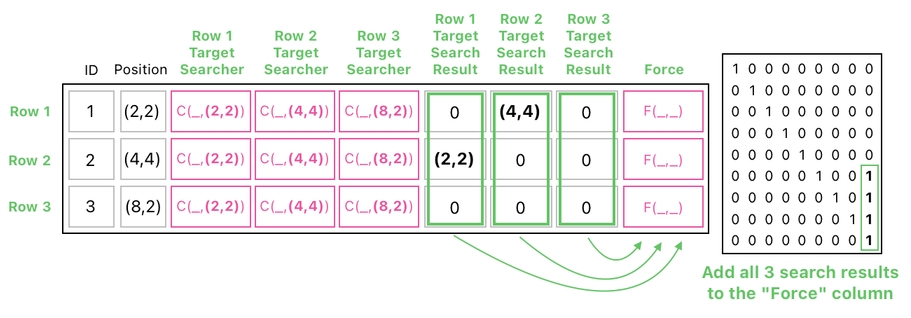
Our next goal is to generate forces by means of this "F" function. For this purpose, we will first need to add an extra column to our data table, and fill it with "F(_,_)".
This is where we will start constructing force vectors. First, let us add our search results to the column of "F" functions, by means of the multiplication shown below.
This will result in the following table, in which the "F" functions are now partially filled out.
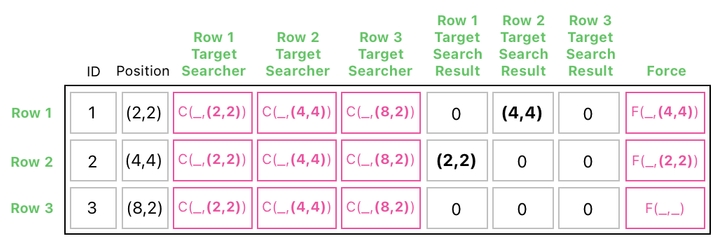
The "F" function inside the 3rd row, though, still has its second argument left as unknown because nothing was added to it (adding 0 is the same thing as adding nothing).
Next, let us add our circle's positions to these partially filled "F" functions:
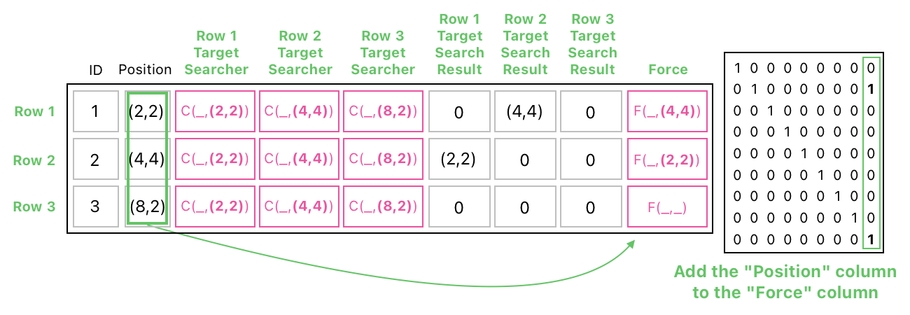
Can you guess what it's about to do? Yeah, you got it right (probably). The positions, (2,2) and (4,4), will fill out the remaining underbars (_) of their respective "F" functions.
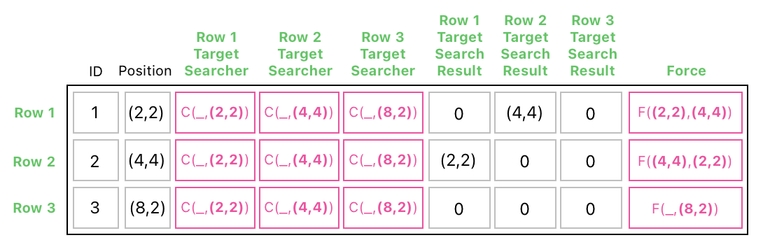
Now, how shall we evaluate these resulting "F" functions? Indeed, it is possible for us to come up with an algebraic formula which will tell us how "F" should be computed, but it takes too much time to go through such a process.
Therefore, let us simply assume for now that "F((2,2),(4,4))" evaluates to (-1,-1), while "F((4,4),(2,2))" evaluates to (1,1) and "F(_,(8,2))" evaluates to (0,0).
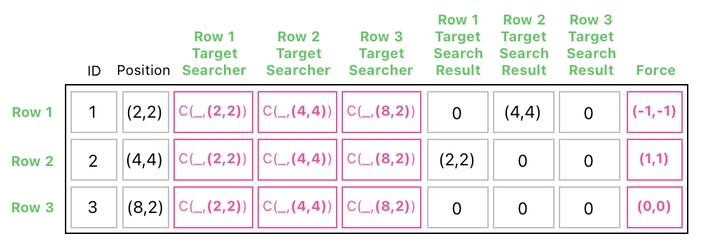
These are the force vectors which will be responsible for "pushing" circles away from each other, so that they can practice social distancing. In order to make that happen, let us add these forces to the current position values (via the multiplication shown below).
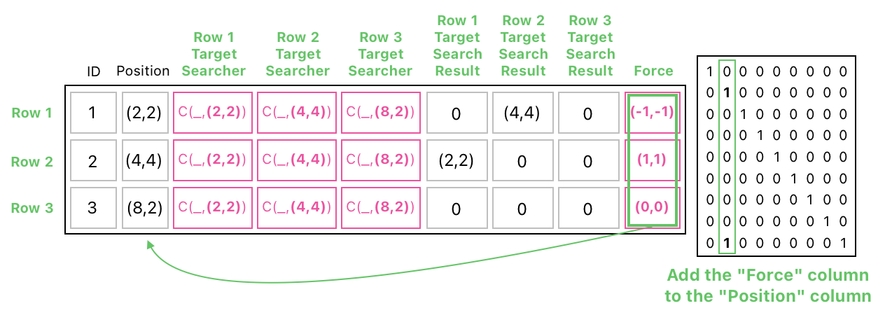
This will update the positions of our two colliding circles.
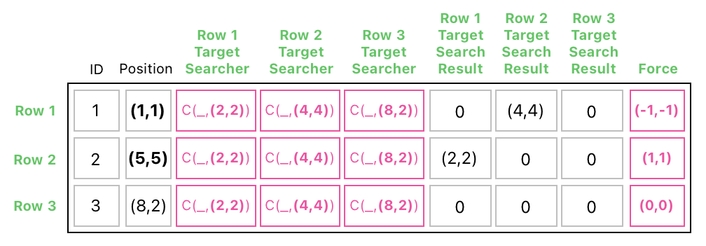
As you can see in this table, 2 events happened due to collision:
(1) The circle at (2,2) got pushed by the circle at (4,4), thereby being relocated to (1,1).
(2) The circle at (4,4) got pushed by the circle at (2,2), thereby being relocated to (5,5).
 Previous Page
Next Page
Previous Page
Next Page

© 2019-2025 ThingsPool. All rights reserved.
Privacy Policy Terms of Service