
Author: Youngjin Kang Date: October 29, 2025
This article is Part 21 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
So far, we have been dealing with an imaginary scenario in which a group of frogs were simultaneously attacking one another.
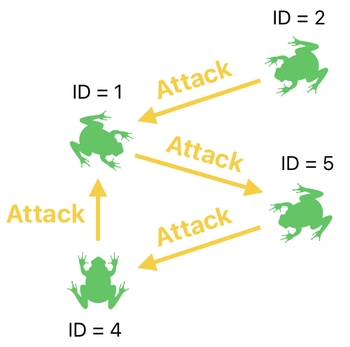
And we have clearly seen that it is possible to process such instances of attack in parallel, by means of matrix multiplications.
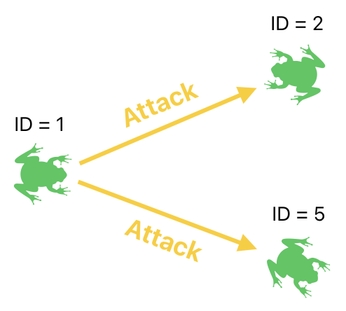
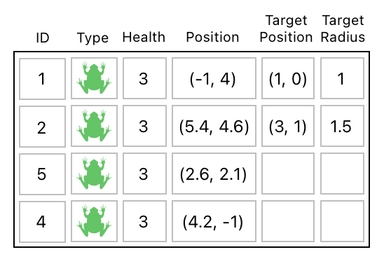
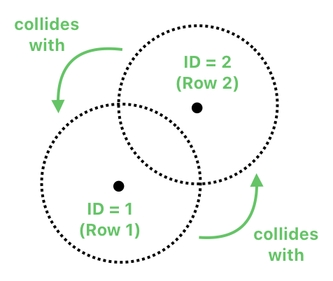
There may as well be, however, cases in which a single frog happens to be attacking more than just one frog, as illustrated in the diagram below.
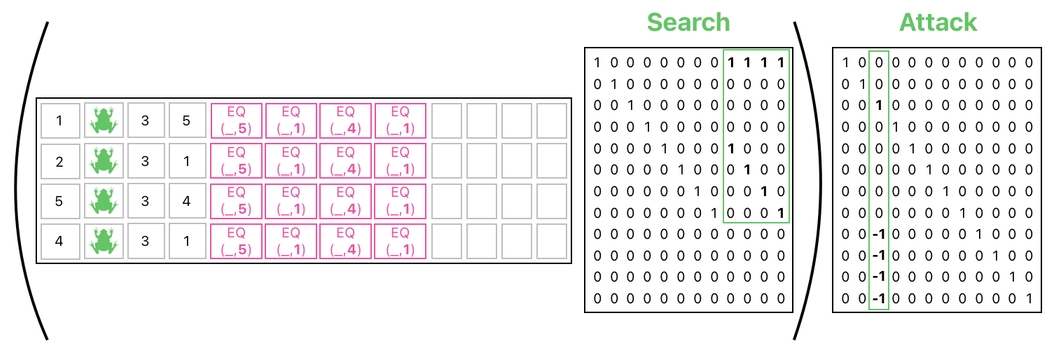
Obviously, we are unable to represent this kind of action in our current table. It has only one column for storing target IDs, which implies that each frog can hold only up to one target at a time.
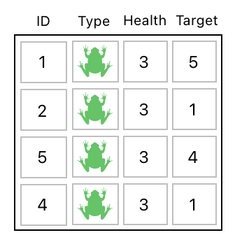
A direct solution to such a problem, of course, is to simply add an additional column to let each frog store up to 2 target IDs at a time.
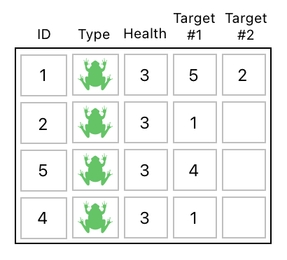
This approach is not scalable, though. What if a frog wants to attack 3 other frogs at a time? What about 4? 5? Or even, 100? Shall we add 100 new columns to our data table just to let a frog attack 100 other frogs?
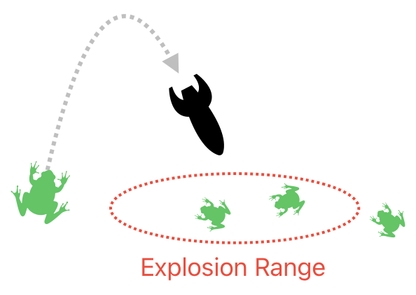
What I just mentioned is not an overstatement. Concepts such as "area damage" and "splash damage" are pretty common in video games, and it is not hard to imagine a gameplay scenario in which a single attack move (e.g. a drop of a bomb or a magic spell) manages to wipe out an enormous number of lives.

And we obviously do not want to write down the target ID of every single one of the victims each time such a massacre happens, do we?
Instead of specifying individual targets, therefore, we need to employ a generalized means of handling victims and their appropriate consequences. For instance, we may consider defining the "target" of an attack not as a collection of specific targets, but as an area in space in which damages should occur (e.g. bomb's explosion range).
How? Oh, it's easy. A quick example is to model such an area as a circle, and represent it in terms of its center position (i.e. X and Y coordinates) and radius.
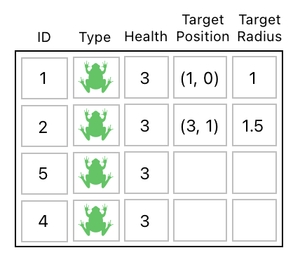
In a graphical sense, this sort of design can be interpreted in the manner shown below. As you can see from the graph, each attack is now being imagined as a circular area of impact.
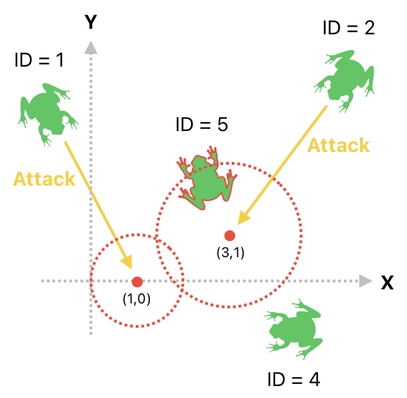
But of course, we still need a way to determine which frogs are supposed to be affected (damaged) by such areas. The logic is straightforward; just look for those who happen to be located inside one of these circles. In order to formulate an algorithm for it, however, we will need to make sure that each frog possesses its own position (i.e. X and Y coordinates of its body) as well, so that we can check to see if the position is inside a circle.
Now that we are provided with enough geometrical data, we can then proceed to extend our table with special columns which can be utilized for conducting searches and storing their results, and so forth.
This particular example of handling area effects, however, is a bit too complicated for a beginner to follow. Therefore, I will start with a much simpler (and more fundamental) example, which is commonly known as "collision detection".
Collision is one of the most important mechanics in video games. It allows us to have physical objects in our virtual universe - objects which continually try to push each other away, so as to make sufficient room for themselves.
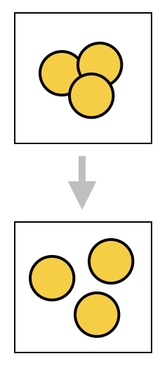
And in order for such a mechanic to work, we need a way to tell which objects are colliding with which.
We can imagine collision as some kind of area effect, where "area" means a volume in space which is being occupied by an object (aka "hitbox" or "collider" in video game nomenclature). When a pair of objects get too close to each other, their areas begin to intersect, in which case it can be stated that these objects are "colliding".
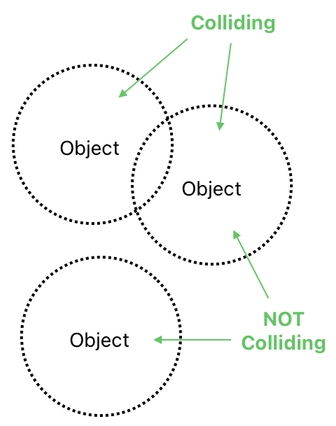
The problem of detecting collision, therefore, can be defined as a task of finding out areas which are intersecting with one another.
How shall we do it, then? There are indeed a variety of methods of solving such a problem, and the adequacy of each one of them depends on multiple factors such as the object's shapes, their distribution, whether they move or not, and so on.
For the sake of simplicity, however, I will stick to something easy for the time being. Let us imagine, for now, that there are 3 circles of uniform radius in two-dimensional space (See the graph below).
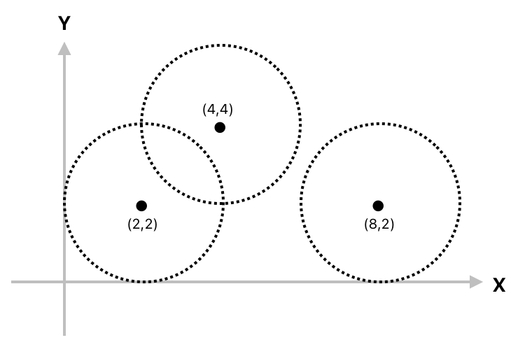
Each of them has the radius of 2. And as you can immediately tell, the two circles on the left are colliding because their areas are overlapping, whereas the other circle on the right is not undergoing any collision at all.
Okay, we are clearly able to tell which circles are colliding just by looking at them, but the thing is that it is not our desire to detect collision manually like this. We need to automate this process, in a way similar to what we did with the case of frogs attacking each other.
For a systematic solution, we will first need to mark every one of our circles with a unique ID, like the ones displayed here:
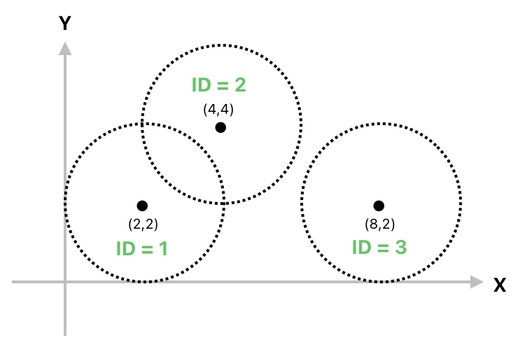
This will let us express these 3 circles as 3 rows in a data table, which is shown below. The table has three columns, which denote the ID and the (X,Y) coordinates of each circle respectively.
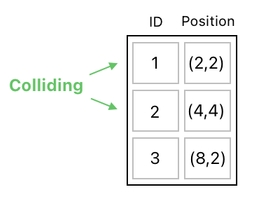
Our goal is to let the system figure out the fact that circle-1 and circle-2, which correspond to the first and second rows of the table, are colliding with each other.
To make this into reality, we must first come up with a rule for telling whether two circles are colliding or not.
Remember that, in our example, every circle has the radius of 2. This means that, the very moment a pair of them touch each other, their distance will be 4 (See the picture below).
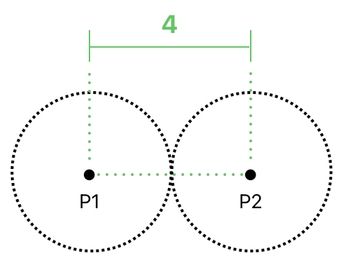
Whenever the distance becomes less than 4, the two circles will be colliding. And whenever the distance becomes greater than 4, they will stop colliding.
If we refer to their center positions as P1 and P2, then, we will be able to define our collision rule (abbreviated as "C") as the following:

The value of "C(P1,P2)" tells us whether a pair of circles of radius 2, whose center positions are P1 and P2 respectively, are colliding with each other. "1" means they are colliding, whereas "0" means they are not.
Whenever P1 and P2 are equal, we know that they must both be indicating the same exact circle (unless we assume that multiple circles are able to coincide at the same location). Since a circle cannot collide with itself, we can say that collision happens only when P1 is NOT equal to P2.
The "dist(P1,P2)" function gives us the distance between P1 and P2. As mentioned earlier, two circles collide whenever the distance between their center positions is less than 4. This can be expressed as "dist(P1,P2) < 4".
All right, then. With this new definition called "C(P1,P2)", what shall we do to detect collisions? The answer is, it is not so different from what we did with the frogs attacking each other. We just need to extend our table and fill it with the appropriate search criteria and results.
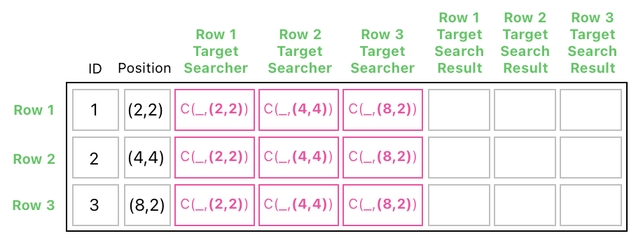
In this new scenario, though, we will no longer use the "EQ" function because we are not searching for the IDs. Instead, we will use the "C" function I just introduced above, in order to be able to tell whether two circles are colliding or not.
We can then proceed to fill out the "P1" part of "C(P1,P2)" by adding the 2nd column (i.e. "position" column) to the 3rd, 4th, and 5th columns in parallel, and assigning their results to the 6th, 7th, and 8th columns, respectively. This process can be carried out by means of the multiplication shown below.
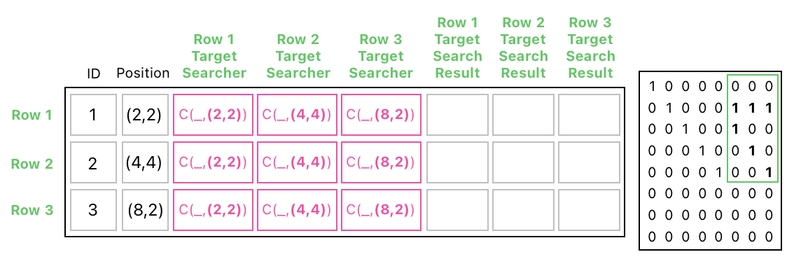
This produces the "search result" of our collision detection scheme, which is shown here:
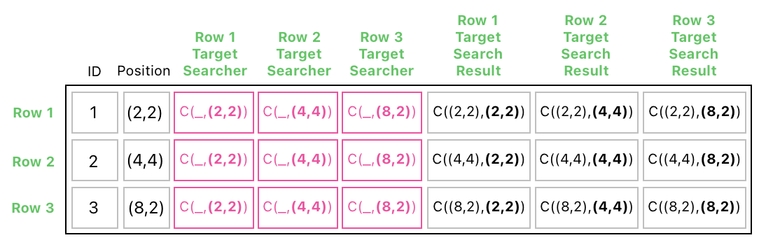
which evalutes to:
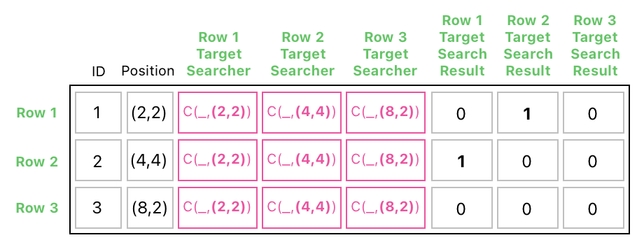
Here is how it should be interpreted:
(1) The 1st row's circle is colliding with the 2nd row's circle because the 2nd row of "Row 1 Target Search Result" is set to 1.
(2) The 2nd row's circle is colliding with the 1st row's circle because the 1st row of "Row 2 Target Search Result" is set to 1.
 Previous Page
Next Page
Previous Page
Next Page

© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service