Back

Home/Library/Concepts of a Plan (2025)/Linear Algebra for Game Development - Part 20

Linear Algebra for Game Development - Part 20

Author: Youngjin Kang Date: October 26, 2025

Before You Read

This article is Part 20 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.

Processing Multiple Targets

Last time, we saw that it is possible to let the system automatically generate a basis which can be used to find any number of existing targets in our game. That is, we saw that there is a way to extend a table which looks like this:

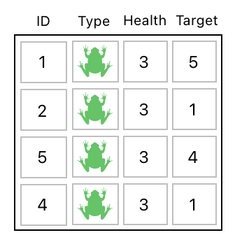
Linear Algebra for Game Development - Part 20 (Figure 1)

into something which looks like this:

Linear Algebra for Game Development - Part 20 (Figure 2)

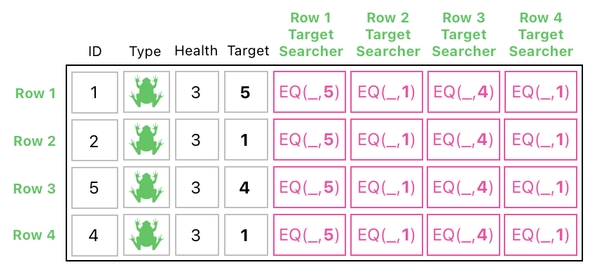
The right half of this table (i.e. 5th, 6th, 7th, and 8th columns) is a basis for processing the targets. For the sake of understanding the reasoning behind this, let us review the scenario which our table is illustrating.

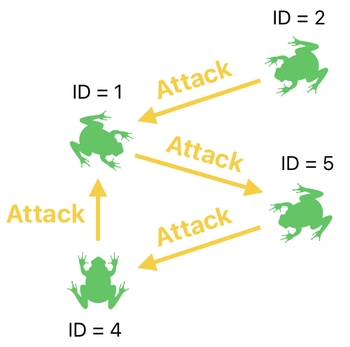
Linear Algebra for Game Development - Part 20 (Figure 3)

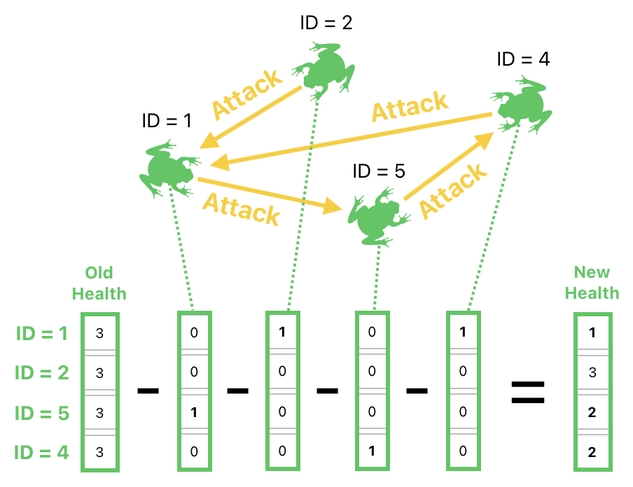
As the picture suggests, 4 frogs in our game are simultaneously attacking each other. Every one of them has its own attack-target, which is represented by one of the "target" ID values in the 4th column of our data table.

What shall we do with these targets?

Oh, for sure, we want their attacks (i.e. damages) to be applied to their appropriate targets. The picture below shows who's attacking whom, and how these frogs' health numbers should change once the attacks are over.

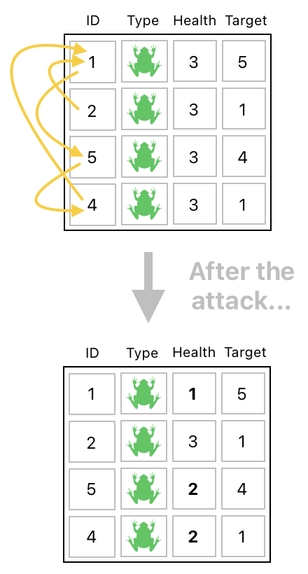
Linear Algebra for Game Development - Part 20 (Figure 4)

Let us assume that each attack deducts 1 from the target's health. Given this, we are able to say that frog-1's health will be reduced by 2 because BOTH frog-2 and frog-4 are attacking frog-1 at the same time. Frog-2's health will stay the same because it is not being targeted by anyone else, whereas frog-5 and frog-4 will each have its health reduced by 1 because each of them is being attacked by one other frog.

How to automate this kind of process?

Since the targets are supposed to be attacked (i.e. receive damage), we know that we need to search for the rows which correspond to these targets, and then move on to reduce their health values. Since there are 4 targets, we will need to search for their corresponding 4 rows and reduce their health values accordingly.

Linear Algebra for Game Development - Part 20 (Figure 5)

And this is where the right half of our extended table (shown above) comes in handy. We can use these 4 extra columns to look up and update not only a single frog (row), but all 4 of them.

In order to search for all 4 targets in parallel, we must first append 4 additional columns to our table in order to make room for the search results.

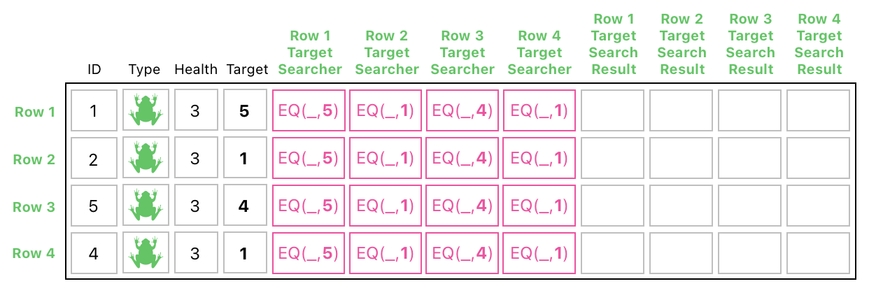
Linear Algebra for Game Development - Part 20 (Figure 6)

The way we carry out the searching process is the same as what we saw in the previous article, but this time we will be executing the same type of calculation 4 times, in the manner shown below.

Linear Algebra for Game Development - Part 20 (Figure 7)

If we were only searching for row-1's target, we would only need to take the sum of the 1st and 4th columns of the table and declare it as the search result. In our current scenario, however, we are searching for the targets of all 4 of the rows, which means that we need to perform 4 separate searches and group them into 4 columns.

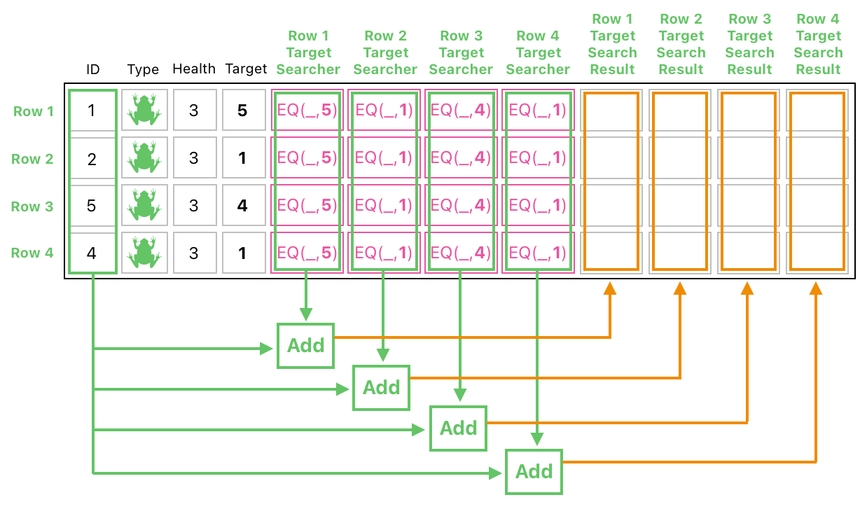
The procedure shown above can be carried out by means of a single matrix multiplication. See the picture below, and you will see how it works.

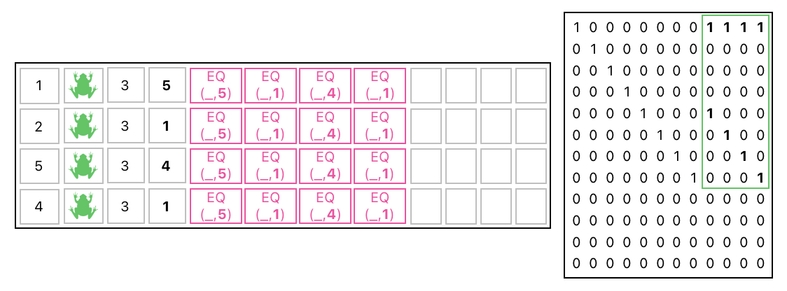
Linear Algebra for Game Development - Part 20 (Figure 8)

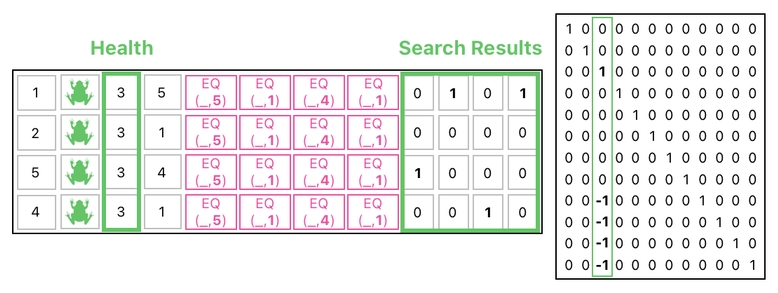
The result of such a computation will be the table displayed below. The "search result" columns in this resulting table, as you can tell, are filled with instances of the "EQ" function which have BOTH of its arguments specified and none of them left as unknown.

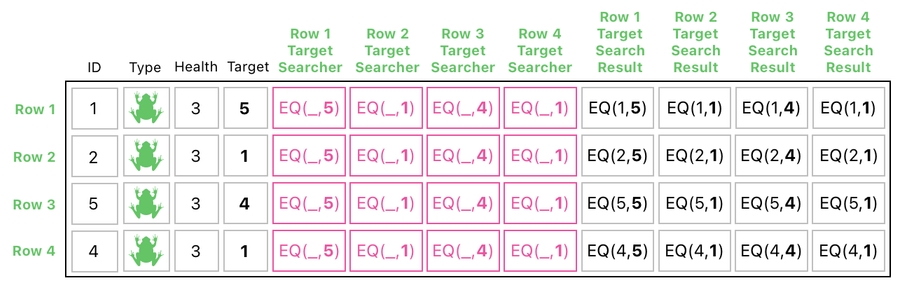
Linear Algebra for Game Development - Part 20 (Figure 9)

Since both of the function's arguments are fully identified at this point, we can simply evaluate the values of "EQ" according to its rule.

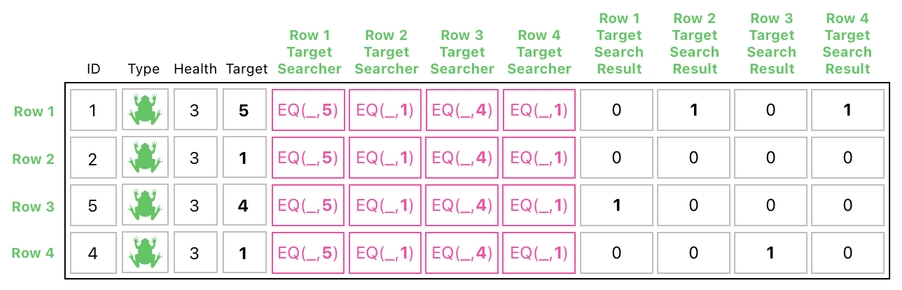
Linear Algebra for Game Development - Part 20 (Figure 10)

This is the result of the searching process, made up of 1s and 0s ("1" means "found" and "0" means "not found"). Let me explain what I mean by this, as well as how to interpret the result shown here.

For the ease of comprehension, I will go over the meaning of the resulting data step by step.

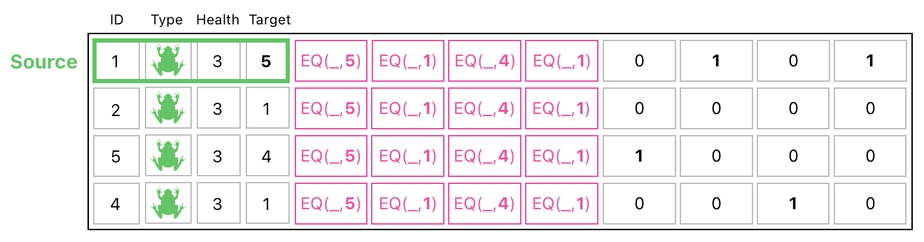
Linear Algebra for Game Development - Part 20 (Figure 11)

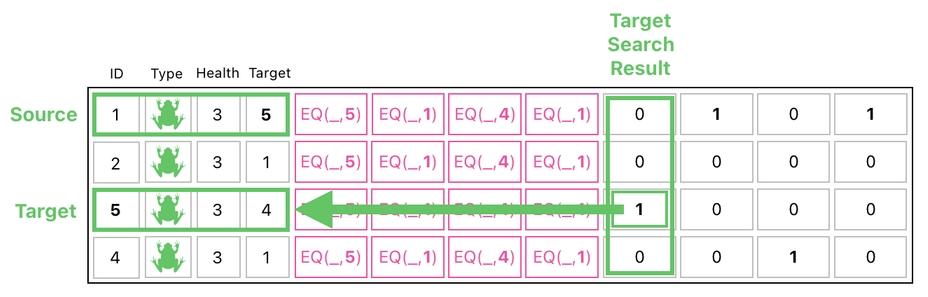
Let us take a brief look at the 1st row of the table, which is representative of the frog whose ID is 1. This can be called the "source" of an attack, as opposed to the "target" who is being attacked by the source.

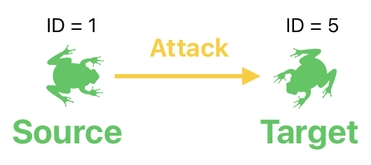
Linear Algebra for Game Development - Part 20 (Figure 12)

And in this particular example, we know that if the source's ID is 1, its target's ID must be 5 because that's what is written in the "target" entry of the source's row.

The thing is, we need an automated (i.e. computational) way of figuring out that the ID of the target is 5 when the ID of the source is 1. For such a purpose, we will take a look at the 9th column in our table. This column denotes the search result for the 1st row's target.

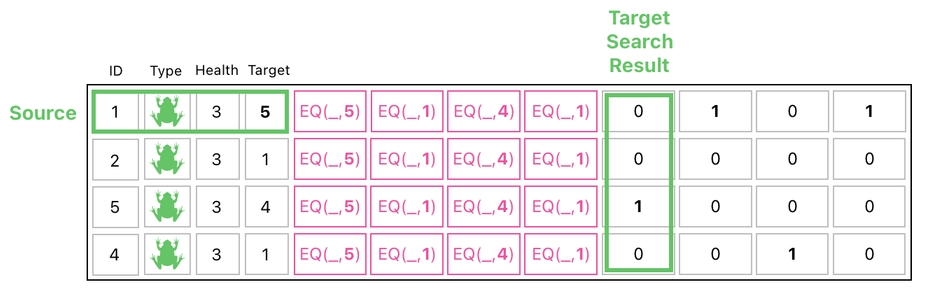
Linear Algebra for Game Development - Part 20 (Figure 13)

This column consists of four binary digits: [0, 0, 1, 0]. What does this mean? Here, I will tell you the meaning of this esoteric sequence of 1s and 0s.

The 1st element of search result is 0. What this means is that the 1st row of the table is NOT the 1st row's target.

The 2nd and 4th elements of the search result are 0s as well, which means that NEITHER of the 2nd and 4th rows of the table is the 1st row's target.

The 3rd element of the search result, on the other hand, is 1. Do you know what this means? It means that the 3rd row of the table must be the 1st row's target.

Linear Algebra for Game Development - Part 20 (Figure 14)

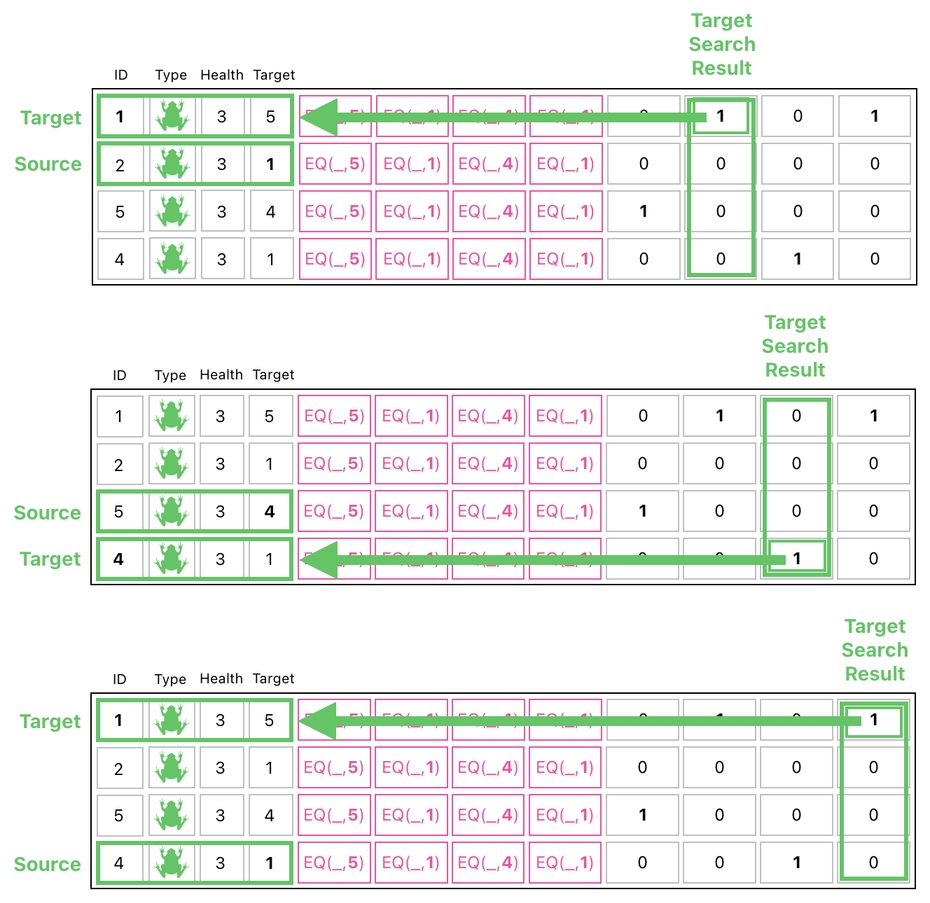
We can apply this sort of interpretation to the other 3 rows (frog) as well. They are displayed below.

Linear Algebra for Game Development - Part 20 (Figure 15)

Parallel Computation

All right. What is the point of having these, then? As you may remember, our ultimate goal is to apply damages (i.e. decrements in health) to the targets. And it turns out that the search results we managed to derive can be used to fulfill such a goal. Let me show you how.

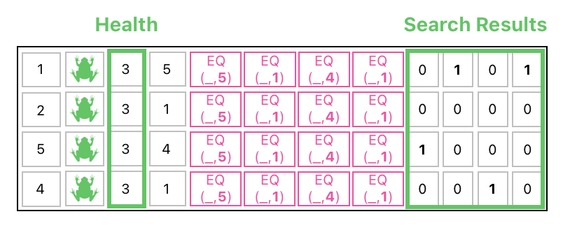
Take a look at the labels shown below. As you can see, the table's 3rd column contains the current health values of the frogs, while the last 4 columns contain the search results of the frogs' respective targets.

Linear Algebra for Game Development - Part 20 (Figure 16)

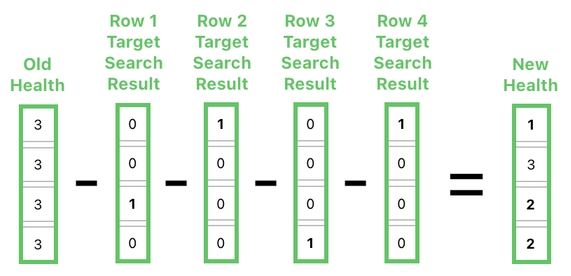
Let me tell you what we are supposed to do to compute the aftermath of the attacks. We first need to grab the column of health values (i.e. 3rd column of the table), and subtract all 4 of the search results from it. If you think about the implication this this process a bit, you will soon realize that the resulting column is the new health values of the frogs after the round of attacks.

Linear Algebra for Game Development - Part 20 (Figure 17)

Here is a breakdown of what is going on here.

First, we subtracted the 1st row's search result from the health values. By doing this, we decremented the health of the frog who was being targeted by the frog in the 1st row.

Next, we subtracted the 2nd row's search result from the health values. By doing this, we decremented the health of the frog who was being targeted by the frog in the 2nd row.

This pattern continued down to the bottom (4th row) of the table, leading to 4 subtractions in total (1 for each source of an attack).

If you are confused, just stare at the picture below for an hour and you will get it.

Linear Algebra for Game Development - Part 20 (Figure 18)

The 4 subtractions I mentioned above can be carried out by means of a matrix multiplication as well (See the image below).

Linear Algebra for Game Development - Part 20 (Figure 19)

Overall, we can summarize the whole procedure of executing multiple attacks into two matrix multiplications. The first multiplication fills out the "search result" columns with their appropriate values (i.e. 1s and 0s), and the second multiplication applies damages to the targeted frogs based upon the computed search results.

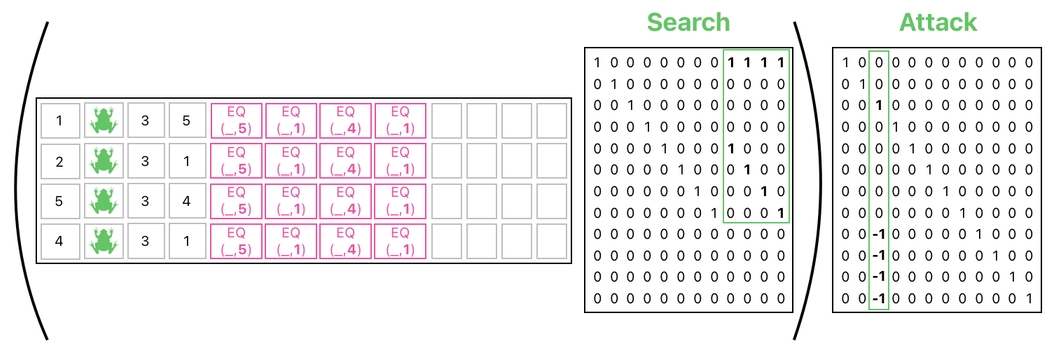
Linear Algebra for Game Development - Part 20 (Figure 20)

And again, the first step of calculation is not really an authentic "matrix multiplication" in linear algebra because it involves a nonlinear function called "EQ". For this reason, I had to put parentheses around the first step to denote that the search must be performed first before applying damages (i.e. that the two matrices, labeled as "Search" and "Attack", cannot be combined into a single matrix).

Previous Page Next Page