
Author: Youngjin Kang Date: October 17, 2025
This article is Part 19 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
In this part of the series, we will continue with the problem of finding a frog by its ID and applying damage to it.
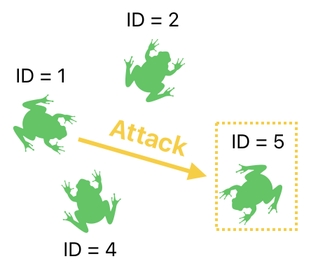
I have recently demonstrated how to spot a specific frog in our game by means of a matrix multication, which yields a "search result" in the form of an array of 1s and 0s.
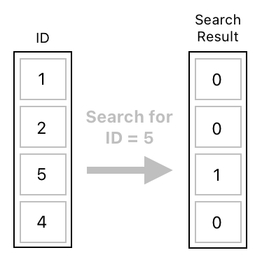
But of course, there is nothing practical we can do with this result alone. In order for the gameplay logic to work, we need to figure out a way of applying our search result to the game's data table in some way or another.
For example, we ought to make sure that the attacked frog (whose ID is 5) will have its "health" value decreased after receiving the attack.
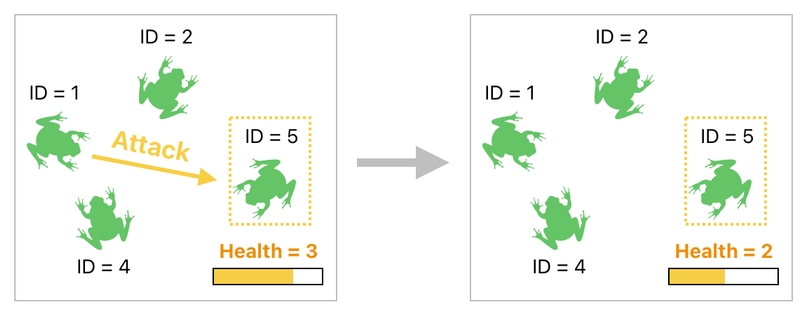
This can be done by selecting the table's row whose ID is equal to 5, and then changing its "health" value to something smaller than what it used to be (Let's say that it is supposed to drop from 3 to 2).
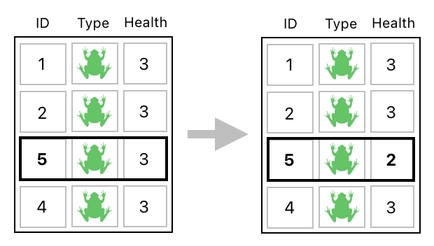
How to implement this kind of mechanic? First of all, we should recall that the process of searching for the ID of 5 requires the addition of a special column, whose entries are all set to "EQ(_,5)".
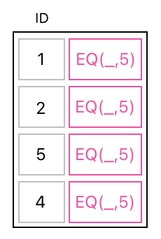
If we wish to modify our data table instead of just looking up a row, though, we ought to do something more than what we did in the previous article.
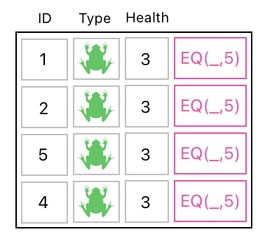
Instead of just taking out the column of ID values from the table and applying a search process to it, we must take the entire table and append our search result to it.
Here is how it can be done. First, just leave the data table as it is (without discarding anything) and simply attach our special column to it (as illustrated in the picture below).
Next, add this special column to the column of ID values (which yields the "search result") and append the result of the addition to the table.
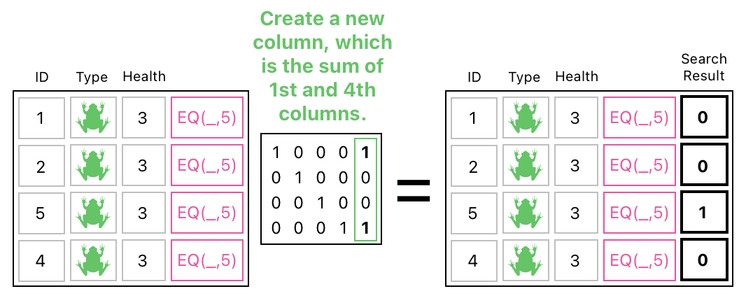
Okay, now we've got our search result as an additional column in our data table. We are one step closer to the final goal.
Here is the next step. Let us subtract this search result from the column of health values. Do you see the line of reasoning here?
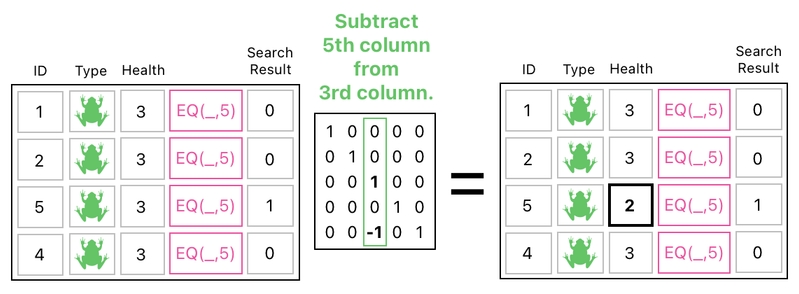
Since the search result is 1 in its 3rd row (which is the row where the ID is equal to 5) and 0 in every other row, subtracting it from the "health" column will subtract 1 from the 3rd row's health value only. This is how we can apply damage to a single frog, whose ID happens to be 5.
The diagram below depicts the full process, which consists of two steps I just demonstrated. The first step performs the search by filling out the last column (aka "search result"), and the second step performs the attack by subtracting 1 from the frog's health.
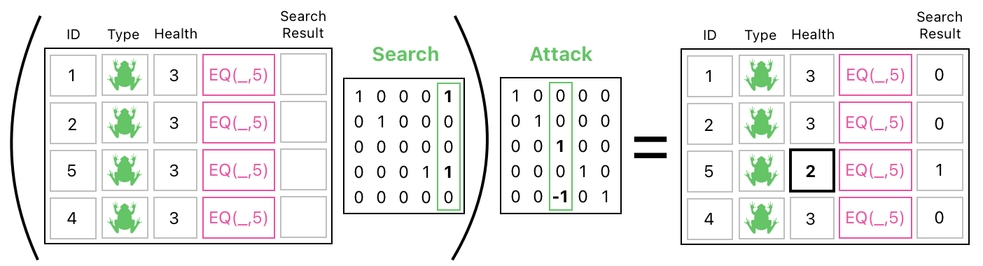
Notice, though, that the first step ("Search") is not a real matrix multiplication in the context of linear algebra.
Since it utilizes a nonlinear function called "EQ", it does not obey the usual properties of matrix multiplication (such as associativity). This is why I had to put the parentheses around the first matrix, for the purpose of denoting that this part of the formula must be evaluated first.
There is still something missing here, though.
In order to find a frog whose ID is 5, we used the special function called "EQ" and supplied the number "5" to it as the second argument. If we were to find a frog whose ID turned out to be 1, for instance, we would have to provide the function with the number "1" instead.
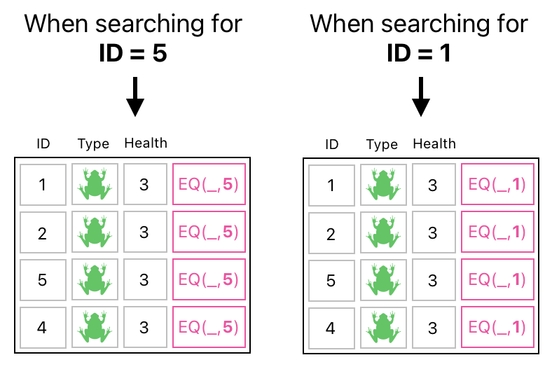
What is so annoying in this kind of approach is that we have to manually fill out the second argument of the "EQ" function every time we are trying to search for an ID.
In order for our gameplay logic to be scalable, we need to automate the task of choosing the desired target in the first place. To illustrate what I mean by this, I will revisit the scenario in which one of the frogs (ID = 1) happened to attack another frog (ID = 5).

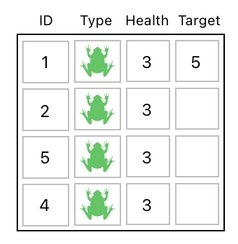
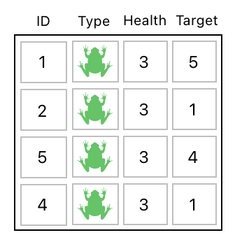
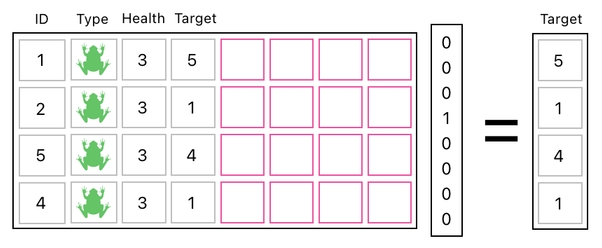
It turns out that, to be able to accurately depict what's happening here, we need a new column in our table called "target". In this column, each entry refers to an ID of a frog which is being targeted. For example, when the target number of the row with the ID of 1 is set to 5 (as in the picture below), it means that the frog whose ID is 1 is currently targeting the frog whose ID is 5.
All right. What if 4 attacks are happening simultaneously (like in the example shown below)?
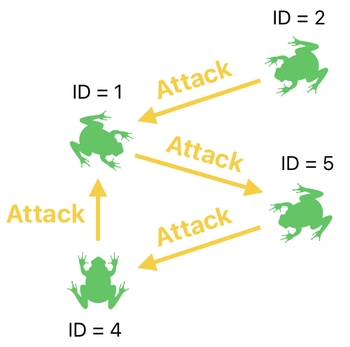
As long as we have a column called "target" in our data table, this sort of parallelism is not tricky to express at all. All we have to do is just specify all of the 4 target IDs in their corresponding "target" entries.
But of course, this kind of representation alone does not accomplish anything useful. We need to figure out how to find and access these targets, so as to be able to apply the appropriate effects (e.g. damages) to them.
Since there are multiple targets coexisting in our example, it is not enough to search for just a single ID in our table.
For example, we might consider having an extra column, filling it with the "EQ" function, and then using this column to search for an ID.
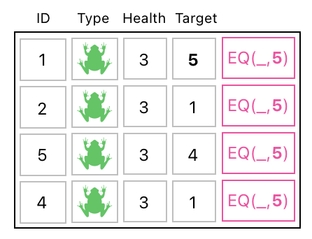
This, however, is not enough when it comes to finding multiple targets. The extra column shown above, for instance, can be used for finding the target whose ID is 5, but it cannot be used for finding the other 3 targets whose IDs are 1, 4, and 1, respectively.
So, what should we do? Without a glimpse of hesitation, I would say that we need a multitude of such extra columns whenever we are looking for multiple IDs at once. Since there are 4 targets in our scenario, we will need 4 columns, each of which is carrying each row's target ID.
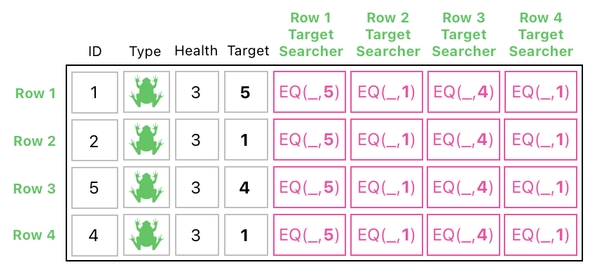
Okay, but we do not want to manually fill out these columns. Targets may change over time, and it will be too cumbersome for us to regularly intervene to keep these columns up to date. The system needs to do it automatically instead.
But how? Here, I will show you how the full procedure can be automated.
First of all, forget about the content of the extra columns and leave them as empty for now. It is because we are not the ones filling them out; we ought to let the system do that instead.
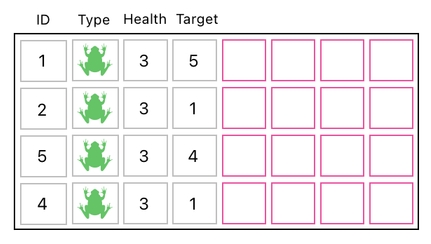
In order to solve this problem, we will first grab the column of target IDs from our data table.
Now, before continuing further, let me introduce an additional rule for evaluating the "EQ" function (We will need this for our next step). Take a look at the expression below, where both of the function's arguments are underbars (_).
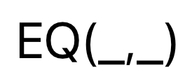
This means that both of the function's arguments are unknown. Whenever we encounter such a case, we shall be following the two rules stated below:
(1) Whenever a function with two unknowns undergoes an addition, we must simply replace rightmost unknown with what is being added.
(2) Then, if the result of the addition undergoes yet another addition, we must replace the remaining unknown with what is being added in this new addition.
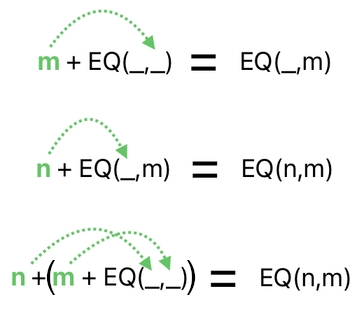
With this in mind, let us take the product between the column of target IDs and a row which is filled with "EQ(_,_)".
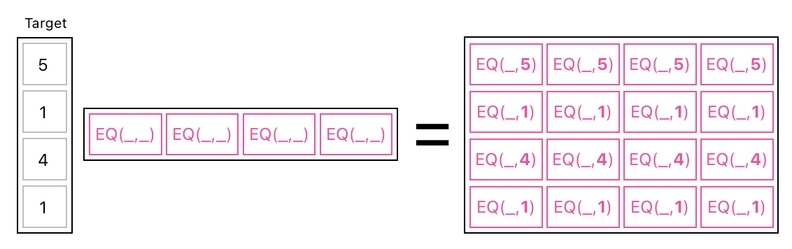
As you can see in the picture above, such a multiplication yielded a two-dimensional array of permutations between the target IDs and "EQ(_,_)", where each instance of "EQ" has its rightmost underbar replaced by one of the target IDs.
The next step is to take the transpose of this result. This will turn all of its rows into columns and columns into rows.
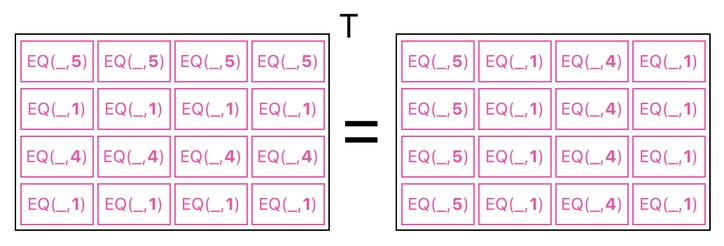
See? Now we are almost there. The result we just got is exactly the same thing as the right half of the data table we are seeking to construct. The only remaining work is to insert our result into the appropriate place.
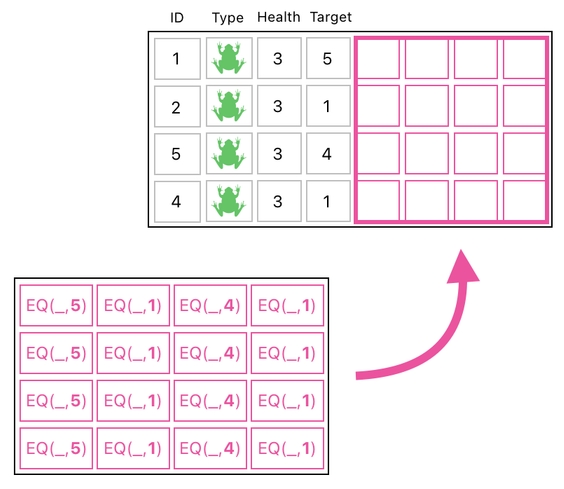
In order to do that, we need to add 4 empty columns on the left side of our result,
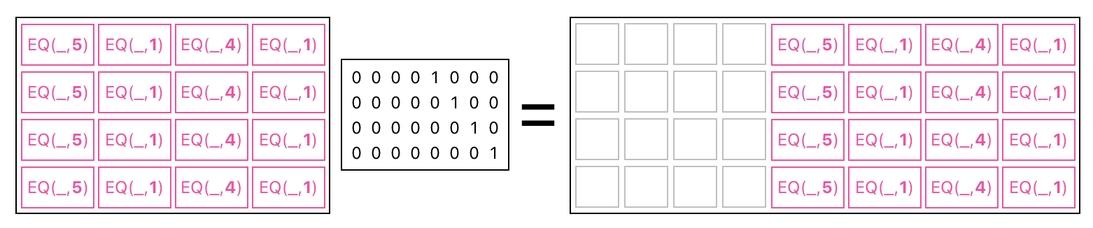
and then simply add this extended thing to our original data table.
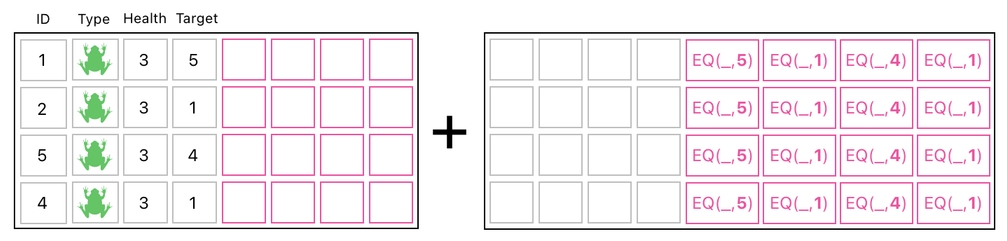
The result of this addition is the table we have been seeking to obtain.
 Previous Page
Next Page
Previous Page
Next Page

© 2019-2025 ThingsPool. All rights reserved.
Privacy Policy Terms of Service