
Author: Youngjin Kang Date: October 13, 2025
This article is Part 18 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
I have hitherto introduced quite a variety of gameplay concepts, such as birth/death, score calculation, winning condition, and so on.
There is one important topic which is yet to be discussed, though - the problem of establishing unique identities.
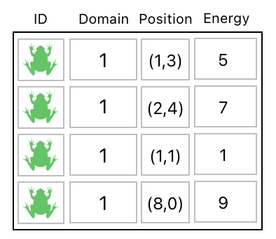
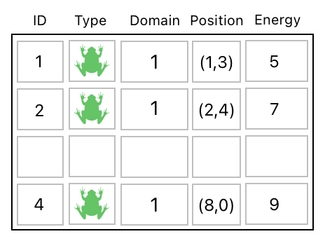
The table above defines a game world which consists of 4 frogs. These 4 frogs share the same exact identity (ID), symbolized by the the green frog-shaped icon.
Does this shared representation suffice in the context of the game? The answer is, it depends on how sophisticated the game is.
If it is okay to let these frogs be anonymous (i.e. not distinguishable from one another), we will happily stick with what we have been doing. In contrast, if it happens to be necessary to ensure that each one of these frogs be unique, we will need to assign a distinct ID to each frog. Let's say that each ID is a positive integer (Think of it as a personal identification number).
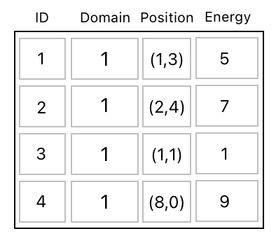
Oh, but we still have to specify that these creatures are frogs rather than something else. Therefore, we will need two separate columns of data to represent our frogs - one for uniquely identifying them, and another one for classifying them as frogs.
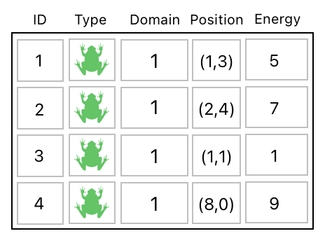
See? Here is a new column called "Type", which tells us what type of object the row is supposed to represent.
In the table above, the 1st row indicates a frog whose ID is 1, the 2nd row indicates another frog whose ID is 2, and so forth. The 4 rows represent 4 frogs, yet they are all unique because they all have different ID values.
At this point, one may ask:
"Okay, what's the use of the ID value, then? Shouldn't the uniqueness of the row itself suffice when it comes to distinguishing one frog from another? Why not just assume that the 1st row corresponds to ID = 1, the 2nd row corresponds to ID = 2, etc?"
This makes sense, but only up to a certain extent. Suppose that we decided to destroy one of the frogs (Not just kill, but completely destroy). This means we will erase the data from the frog's row.
Let's say that the frog with the ID of 3 was destroyed, meaning that we no longer have this frog in our game world.
Imagine, now, that we made a decision to create a brand new frog. What shall we do to express it in our data table? Obviously, it is natural to allocate the 3rd row (which has been emptied out) to this new frog.
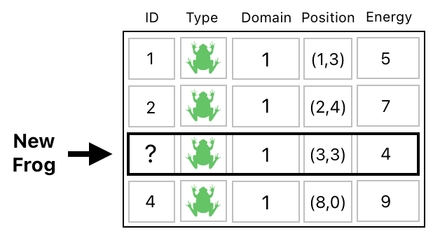
The next question is, which ID should be chosen for this newcomer? It cannot be one of the existing ID numbers (i.e. 1, 2, or 4), since it will break the uniqueness of the IDs. It cannot be 3 either, since it will imply that the new frog is a resurrected body of the one we just destroyed.
This leads us to conclude that we must come up with an ID number which is different from any of the ones we used before. Since the ID of 1, 2, 3, and 4 have been used so far, it will make sense for us to assign the ID of 5 to our new frog.
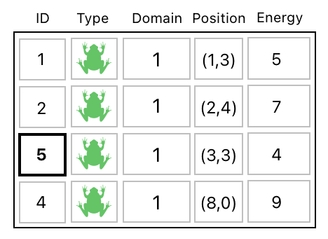
At this point, you can clearly see why we can't just use the row itself as a unique identifier. It is because any row can be repurposed to indicate something other than what it used to indicate.
In our case, the 3rd row used to refer to the frog whose ID was 3. Once this original frog was replaced by a new one, however, we had to mark the row with a new ID in order to distinguish the new from the old. This is why we need to have this explicit identifier called "ID", aside from the uniqueness of the row itself.
There is yet another use case of IDs in our data table.
When playing a game, we often encounter moments in which a character selects another character (an enemy, for example) as its target and triggers some action against it, such as an attack, etc. And whenever such an event occurs, the systems takes the responsibility of applying the appropriate changes to the target such as a reduction in its HP (Health).
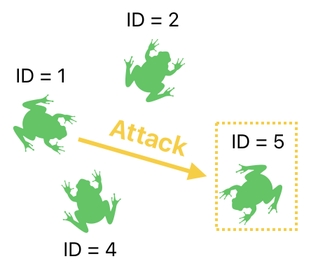
In order for such a selective type of operation to be feasible, we need to ensure that there be some way of finding a character in the table based upon its ID.
How shall we do that? For the sake of simplicity, let us first reformat our table a bit to reflect a scenario in which one of the frogs happens to attack another frog and applies damage to it (e.g. drops its health by some amount). For that, we will just imagine here that each frog possesses only one property called "health" (aside from its ID and type).

The problem we are trying to solve is to find the attacked frog by its ID, and then decrement its health. Let's assume that the attacked frog's ID is 5.
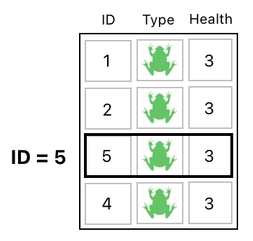
The very first thing we ought to do is search for the row whose ID is equal to 5. And the way we do that? Oh, well! Let us solve this problem step by step. For now, just focus on the table's "ID" column only, and pretend that nothing else exists.
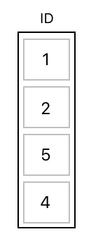
Our mission is simple. Inside this column of IDs, we want to find the entry whose value is equal to 5. And in order to accomplish such a kind of task, we need a new function called "EQ" (shorthand for "Equals").
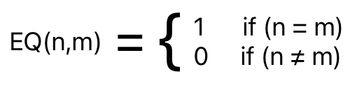
This function takes two arguments, and returns "1" whenever they are equal. If they are NOT equal, it will return "0" instead.
And, do you remember the special algebraic rule I had introduced before? It goes like this: Whenever there is an underbar (_) in place of a function's argument, the previously added term will be transferred into it.
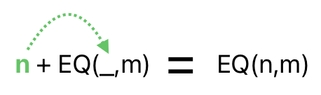
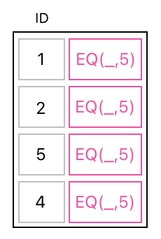
With these constructs in mind, let me attach an additional column to the column of ID values. Every entry of this new column is filled with the expression "EQ(_,5)".
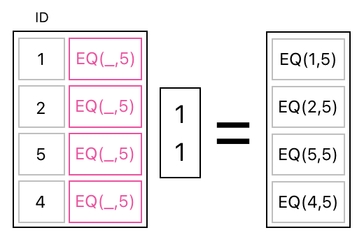
Now, let me add these two columns together by means of a simple matrix multiplication (which is shown below).
Do you see why the result is the way it is here? To clarify, I will show you the full breakdown of how the aforementioned combination of columns yielded "EQ(1,5)", "EQ(2,5)", "EQ(5,5)", and "EQ(4,5)". Take a look at the equations below:

Here is what's going on.
What happens when we add the two columns together? Since the list of values in the first column is [1, 2, 5, 4] and the list of values in the second column is [EQ(_,5), EQ(_,5), EQ(_,5), EQ(_,5)], adding them up will produce a new column which is made up of: [1+EQ(_,5), 2+EQ(_,5), 5+EQ(_,5), 4+EQ(_,5)].
And, guess what? According to the special algebraic rule I have previously mentioned, this particular list of values will transform themselves into: [EQ(1,5), EQ(2,5), EQ(5,5), EQ(4,5)].
Now, it is time to evaluate the value of "EQ" in each of these entries. This final step is straightforward. Whenever the two arguments happen to be identical (as in the case of "EQ(5,5)"), the value becomes 1. Whenever the two arguments differ (as in the case of "EQ(1,5)", "EQ(2,5)", and "EQ(4,5)"), the value becomes 0.
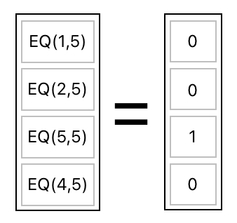
This is it. The resulting column values, [0, 0, 1, 0], is our "search result". We looked for the ID of 5, and the outcome signaled us that the 3rd row is where this ID is located (because the resulting value is 1 in the 3rd row and 0 everywhere else).
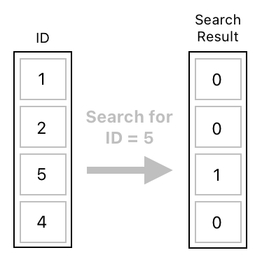
With this result, we can then proceed to select our attacked frog and apply damage to it.
Previous Page Next Page
© 2019-2025 ThingsPool. All rights reserved.
Privacy Policy Terms of Service