
Author: Youngjin Kang Date: October 8, 2025
This article is Part 17 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
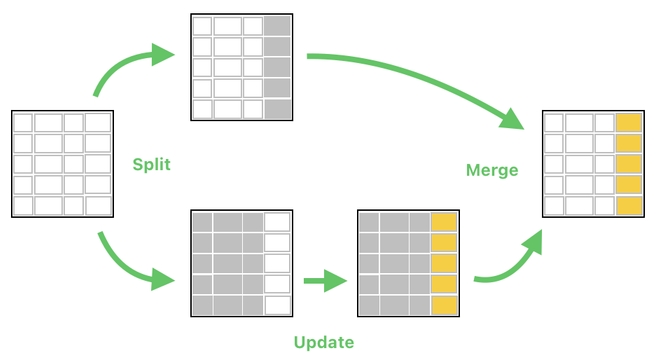
In the previous article, we saw how much of a burden it is to go through a bunch of matrix operations just to modify a single row or column. The picture shown here, for instance, succinctly illustrates how hard it is to update just a single column in a table.
Therefore, we need to come up with a notational shortcut to be able to express such a procedure more elegantly. For this purpose, let me introduce a special superscript which denotes that only a portion of the table should be touched. Take a look at the matrix multiplication below:
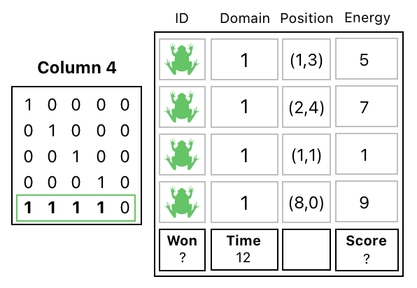
You are probably already familiar with this example. It sums up the table's first 4 rows and assigns the result to the table's last row.
Note, however, that "Column 4" is written right above the matrix. This means that only the 4th column of the data table must be changed when the matrix gets multiplied. Its full algebraic expansion is shown below.
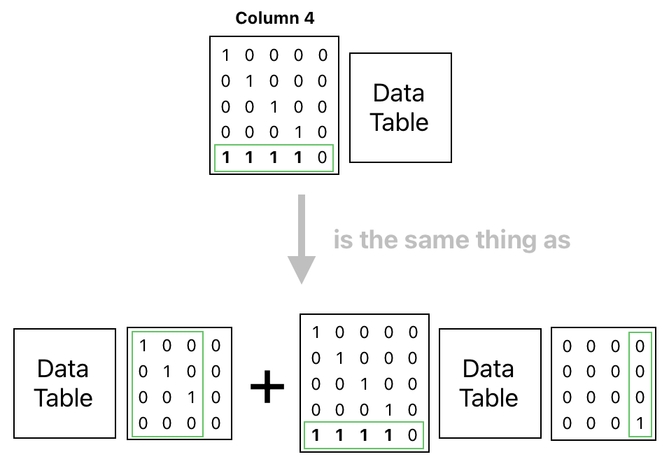
Here, you can see that a "matrix" with the superscript "Column 4" is equivalent to performing two matrix multiplications and one matrix addition.
Of course, it is mathematically wrong to call this a "matrix", since it is a shorthand expression for denoting a multitude of matrix operations. Thus, it makes more sense to say that it is just an unconventional way of denoting what one may refer to as a "matrix function".
The biggest advantage of this new notation is that it allows us to just draw a single matrix to express the concept of partial manipulation.
In the picture below, for example, we can see that a single matrix is being used to denote the process of taking the sum of the frogs' energy values and registering it as the game's score.
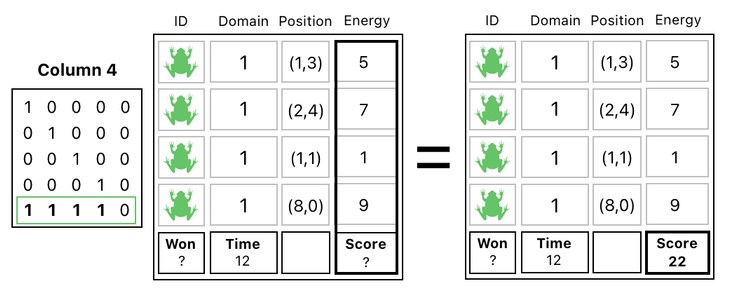
Notice how much easier it is to write it this way, in contrast to what we had done before.
Such a type of syntactic shortcut may also be extended to support any interaction between elements which are diagonally apart.
For the sake of demonstrating what I mean by this, I will revisit one of the previously mentioned scenarios - that of calculating the score AND putting the result in a different column (See the picture below).
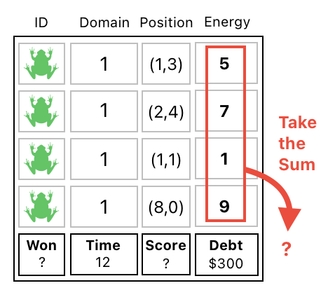
Here, we can clearly see that the "score" slot is located within the column of position values, instead of the column of energy values (from which the score is being derived). So the problem we are facing here is that we must transfer the result of the sum (of the energy values) diagonally, so as to let it land at the very bottom of the column of position values.
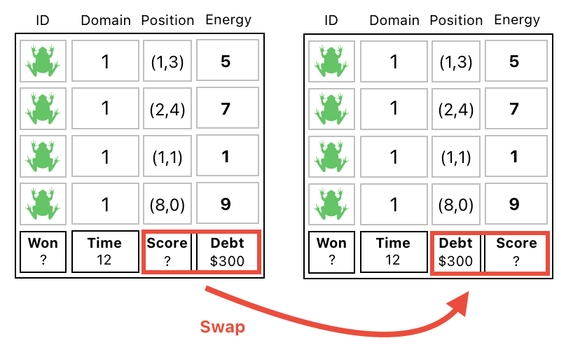
And a way we can accomplish this task has already been illustrated. First, we swap our "score" slot with the one that is right underneath the energy values.
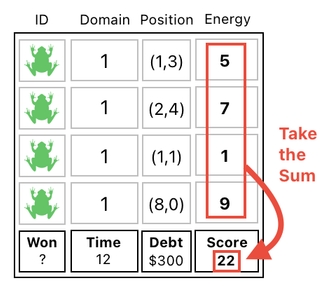
Then, we compute the sum of the energy values and put it into the "score" slot.
Finally, we swap the two slots back in order to recover the table's original format.
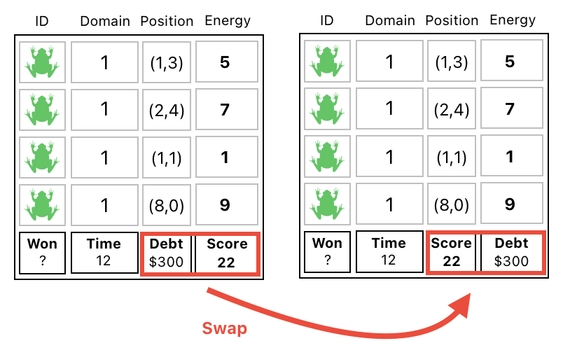
This 3-step process would've been a nightmare to carry out if we still insisted in manually splitting out the table into sub-tables, updating one of them, and then merging them back together in every one of these steps.
Fortunately, we are now equipped with a shorthand notation which lets us express the whole process in a much more elegant manner. In each step, all we need to do is draw a single matrix and attach a notation to it to tell in which portion of the table it is supposed to be operating.
Let me go through this step by step. First, we swap the 3rd and 4th columns inside the table's "Row 5" (5th row).
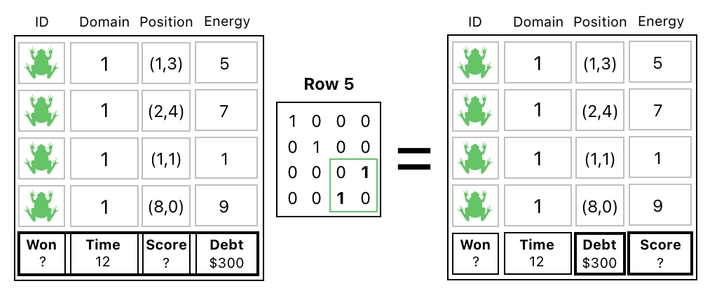
Then, just as usual, we calculate and record the score inside the table's "Column 4" (4th column), by summing up the first 4 rows and assigning it to the last row.
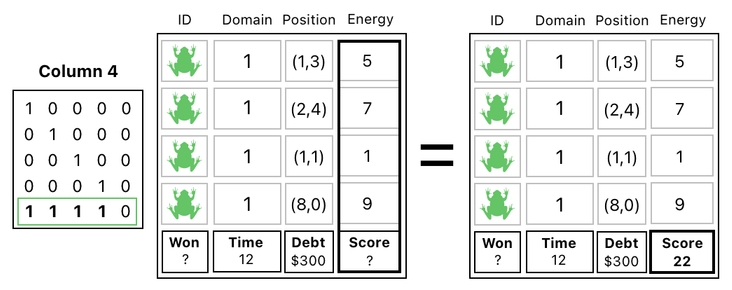
Finally, we swap the 3rd and 4th columns inside the table's "Row 5" (5th row) once again, just like we did in the first step.
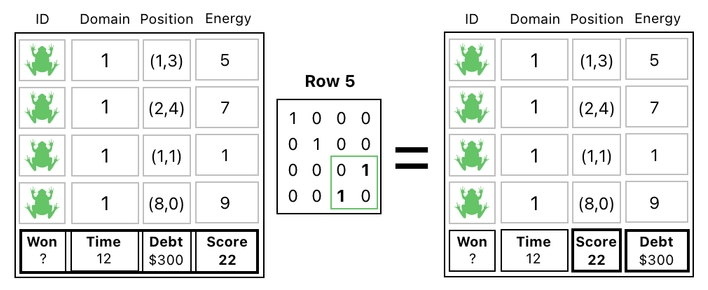
This completes our task of computing the score and putting it in a different column. If we gather all of these steps in one place, we will see something which looks like this:
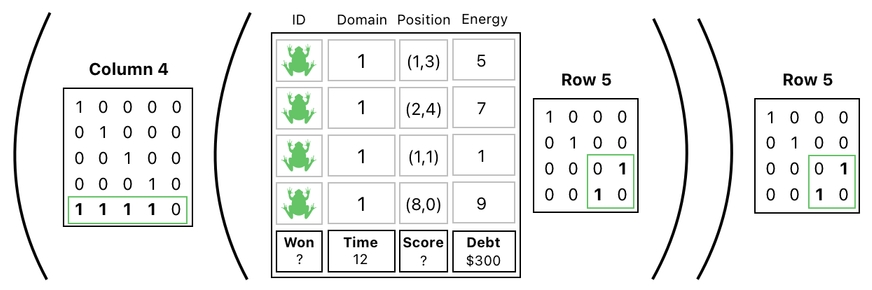
Each curved black line represents a parenthesis.
I am using parentheses here for the purpose of clearly defining the order in which these 3 steps need be executed (i.e. that a swap must happen first, score calculation must happen next, and then another swap must happen last).
Notice that each rectangular block of numbers shown here, while it graphically resembles a matrix, is not really a "matrix" in the algebraic sense.
Therefore, it is erroneous to assume that the properties of matrix algebra must also apply here. For example, it is wrong to suppose that these "pseudo-matrices" are associative in nature (i.e. that their order of multiplication doesn't matter).
This, as you may have noticed already, is the reason why parentheses are necessary in this case.
Let us go back to one of the earliest in-game data structures we've seen in this series of articles - a 2D grid of items. The following image is an example of a 3x3 grid.

The concept of diagonal data exchange, which I have recently illustrated, proves itself to be quite important in the context of a 2D inventory (such as the one shown here). Suppose, for instance, that the player wants to swap the frog with the cheese.
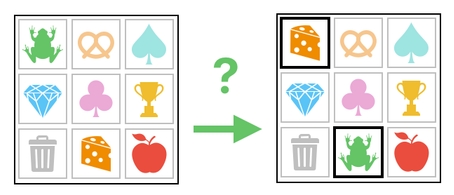
How shall we accomplish this task? Oh, it used to be VERY challenging before the shorthand notation was introduced. Since we are armed with a much more succinct way of expressing movements, however, we can now approach this sort of problem without a rigmarole of painfully verbose algebra.
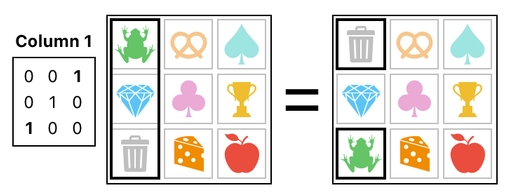
Here is how a quick swap between the frog and the cheese can be done. First, we select the 1st column of the inventory and exchange its 1st row with the 3rd row.
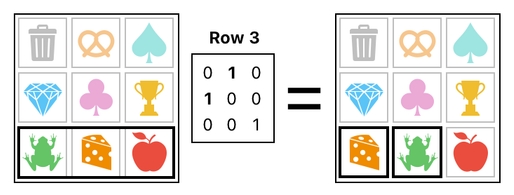
Next, we select the 3rd row of the inventory and exchange its 1st column with the 2nd column.
And then, finally, we select the 1st column and exchange the 1st and 3rd rows again.
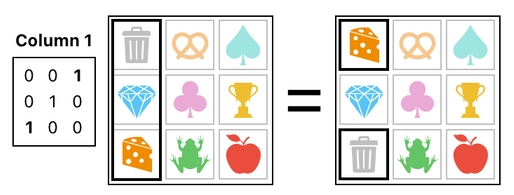
This completes the full swapping process (between the frog and the cheese). The full list of steps is summarized below.
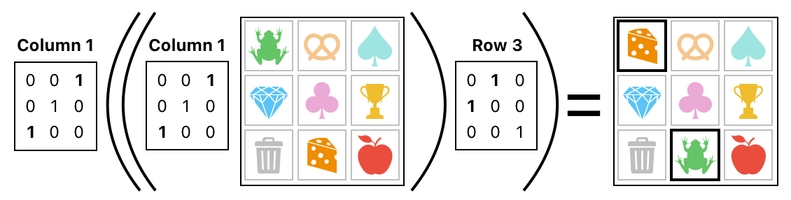
Please beware, though, that what is written here is just one of two possible solutions.
In the method shown above, we made a vertical swap, a horizontal swap, and then another verical swap to generate the effect of swapping the two items (i.e. frog and cheese).
On the other hand, it is also possible to generate the same effect by making a horizontal swap, a vertical swap, and then another horizontal swap instead. What's shown below is the summary of such an alternative solution.
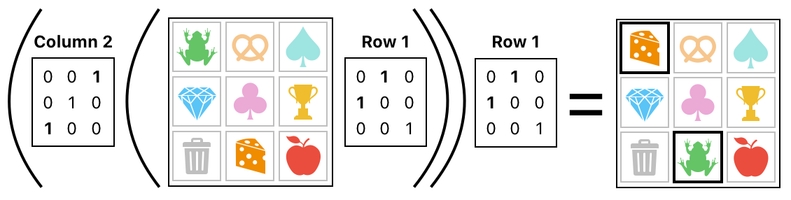
It is not so difficult to come up with a notational shortcut for quickly representing any kind of diagonal exchange. For this purpose, we first need to define the problem clearly.
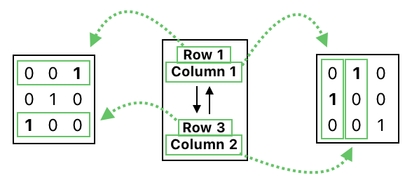
In our example, our frog was located at the 1st row and 1st column of the grid (i.e. "Row 1 Column 1"), and our cheese was located at the 3rd row and 2nd column of the grid (i.e. "Row 3 Column 2"). Our mission was to swap these to locations.

Let us express this particular swapping operation as a block, which contains the two target locations and a pair of arrows denoting the concept of an exchange.
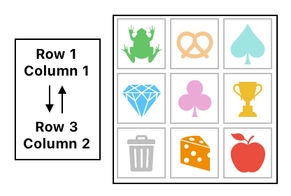
We can then say that this new notation is a shorthand for either one of the two formulas we saw before:
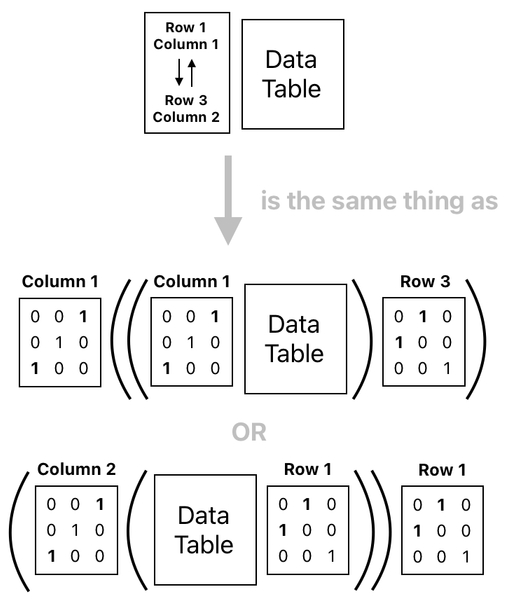
Notice that there are only two distinct matrix expressions in any one of these formulas; one of them is used for horizontal swaps, and the other one is used for vertical swaps. After a bit of observation, you will be able to tell that the exact placement of the 1s and 0s in these matrices directly mirrors the two locations we are swapping.
 Previous Page
Next Page
Previous Page
Next Page

© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service