
Author: Youngjin Kang Date: October 4, 2025
This article is Part 16 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
So far, I have introduced the concept of global properties as well as their use cases in the context of gameplay. The example I came up with was that of the logic involved in determining whether the player has won the game or not, based on the current score.
The next question is, how to calculate the score in the first place? Indeed, we ought to know the score first, in order to make any decision off of it. And to fill out this missing piece of the puzzle, I will demonstrate one possible way of computing the player's score.
Let us revisit our previous table, which tells us that there are 4 frogs in our game world. It is reproduced below.
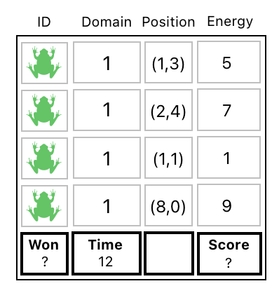
How to determine the current score of this particular game we are playing? Well! It really depends on what kind of game we are playing. Since there are only frogs here, it seems that the score should depend on what these frog are up to.
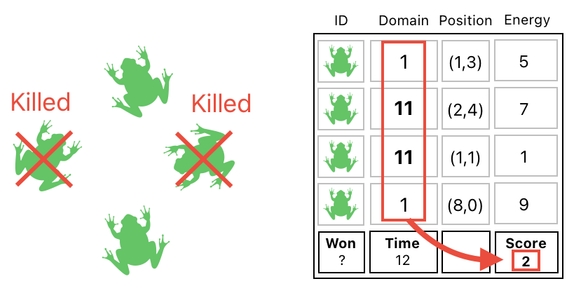
If the goal of this game is to kill as many frogs as possible, it will make sense to calculate the score by adding up the number of frogs who currently reside in Heaven (= 11) instead of Earth (= 1). This is because, when you kill a frog, you are sending it to Heaven.
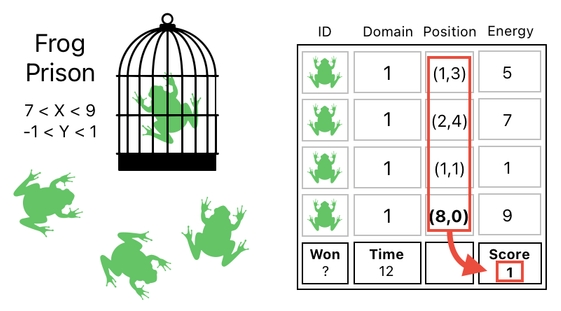
If the goal is to put as many frogs as possible into some kind of "frog prison", on the other hand, we will have to calculate the score by counting the number of frogs whose positions happen to fall within the boundary of that prison.
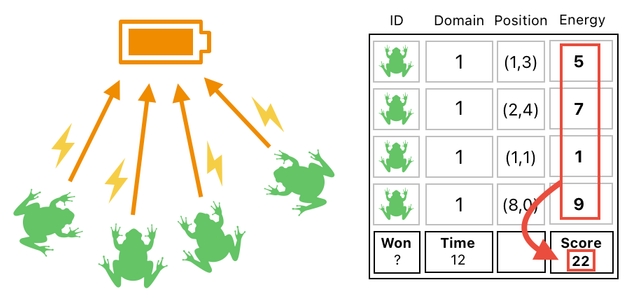
If the game is some sort of "frog power plant simulator" in which your mission is to store as much energy as possible inside your frogs so as to be able to charge your cellphone with them, the score will need to be the sum of all the energy points owned by your frogs.
For the sake of demonstration, let me implement this last scenario.
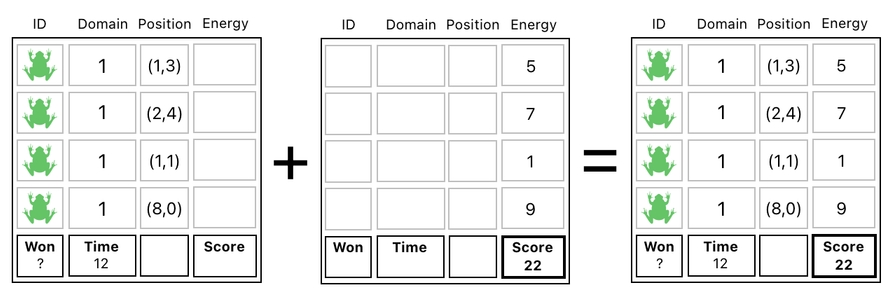
What we need to do to compute the score of a frog-based power generation game is pretty simple on a conceptual standpoint. All we need to do is just sum up the frogs' energy values and put the result in the "score" slot. Easy, isn't it?
A major challenge, though, inevitably reveals itself when we realize that it requires us to fiddle with only one of the columns of the table, and none of the others.
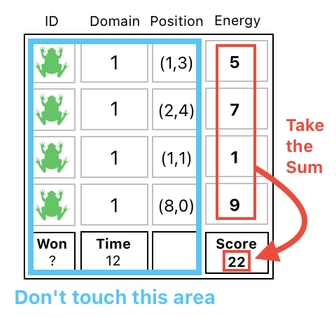
Here, you can see that we are supposed to use only the "Energy" column for computing and storing the game's score. We are not expected to tamper with any other column, for otherwise it will produce nonsensical results.
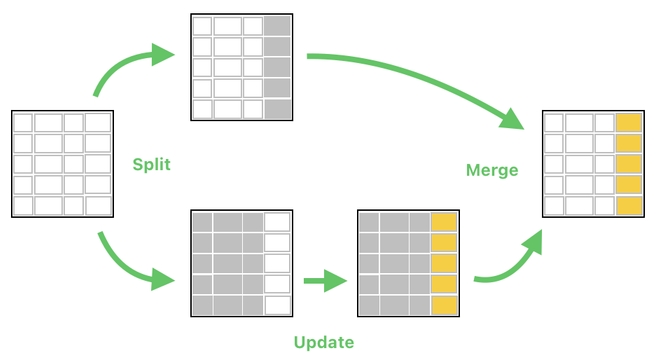
Fortunately, we already know how to handle this kind of problem. All we've got to do is just split our table into parts, process them separately, and then merge them back together.
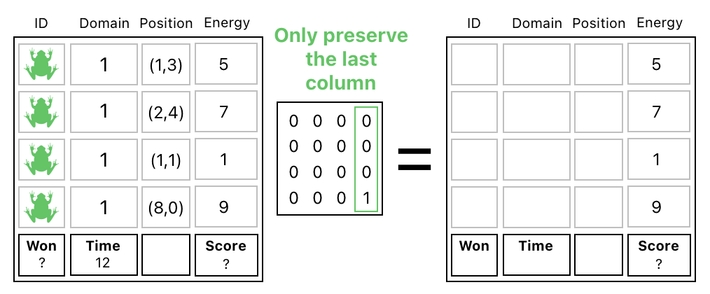
In our case, we want to do something with the "Energy" column only, and keep all the other columns untouched. This means that we need to split our table into two parts - (1) The "Energy" column, and (2) All the other columns.
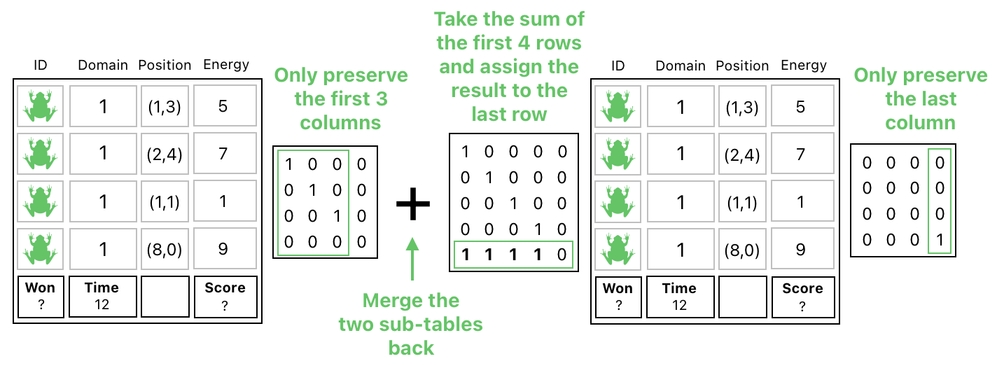
By applying the following matrix multiplication, we can obtain the first part.
And by applying the following matrix multiplication, we can obtain the second part.
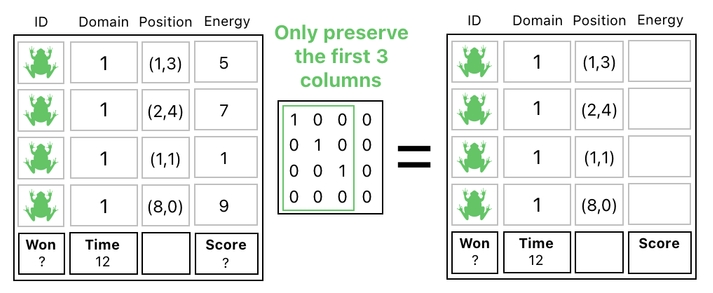
Now that we have the "Energy" column safely isolated from the rest, we are able to sum up the frogs' energy values simply by adding up their corresponding rows. Since only the "Energy" column contains nonzero values here, only the energy numbers will be summed up and nothing else.
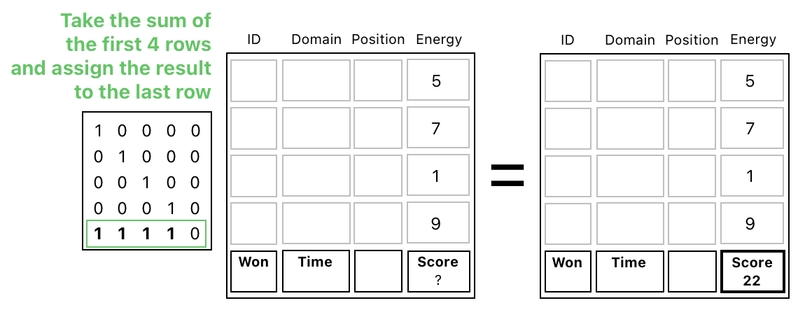
The only remaining step is to combine this intermediary result with the other split part to reconstruct the full table. Here, you can clearly see that the "score" slot of the final result contains the sum of all the energy numbers listed above.
This is just one of many examples of gameplay. The main point, though, is that statistical analysis plays a huge role when it comes to the implementation of game mechanics.
Sometimes it may be as simple as taking the sum or average of a given list of data, or sometimes it may as well be as complex as deriving advanced statistical properties (such as "covariance" or "confidence interval") for the sake of obtaining deeper insights.
Modeling our game world as a table allows us to implement such concepts easily, without taking too much trouble dealing with structural complexities.
The score calculation we just did was fairly straightforward not because it is always guaranteed to be so, but because the particular case we were dealing with happened to involve only a single column. This made it possible for us to just ignore all the other columns.

There could be, however, cases which are more complicated than this. Suppose that the "score" slot happens to be located in a different column. How on earth shall we manage to put the sum of the energy numbers in this location?
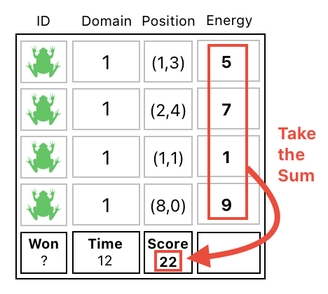
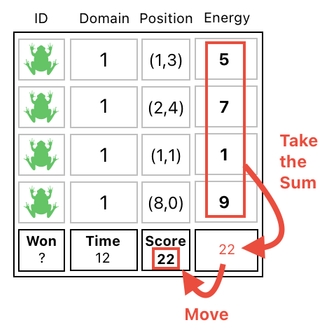
An immediate solution would be to leverage the empty space which is right beneath the energy numbers. You see, the last entry in the column of energy numbers is not filled with anything, so we may just temporarily store the result of the sum there, and then move that value over to the final destination later on.
But, what if there is already something which occupies the space underneath the list of energy values?
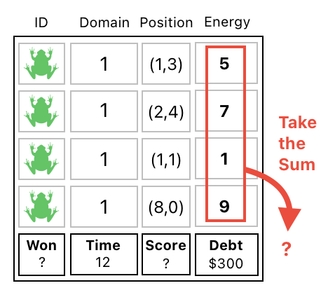
In such a case, we will need to attach an empty row to the table and use it as a temporary storage instead (Think of it as a road, through which things can be transported). This will involve a three-step procedure: (1) Push the value into the storage, (2) Transport the value across the storage, and then (3) Pull the value out of the storage.
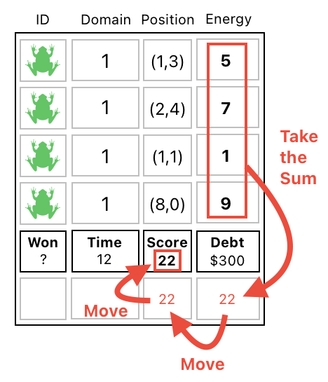
There is a simpler way of doing this, though. Instead of moving the result of the sum downward, leftward, and then upward, we might as well consider temporarily swapping the destination entry with the one which belongs to the "Energy" column, calculating the score, and then swapping it back.
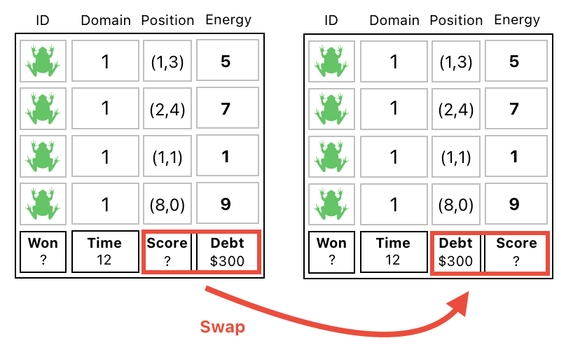
Here is how it is done. We first bring the "score" entry right underneath the individual energy numbers by means of a simple swap.
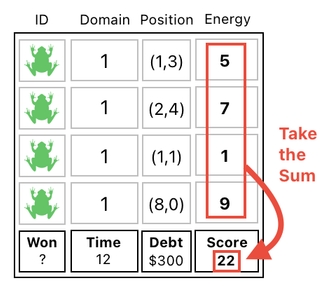
We then take the sum of the energies and store it right underneath them (just as we did before),
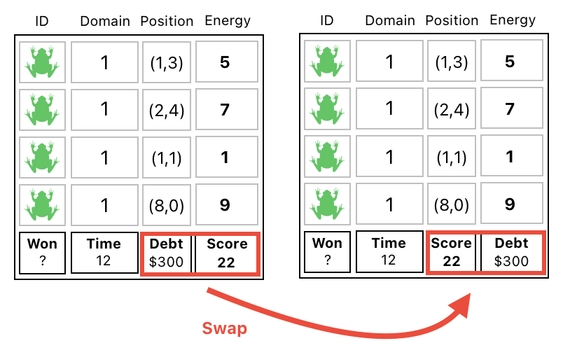
and then bring the updated "score" entry back to its original place by means of another swap.
This alternative method is probably more elegant, since it does not require us to add an extra row to our table just to let it serve as a medium of transportation.
All solutions mentioned so far, however, may feel a bit too painstaking. And you are absolutely right; it is such a pain, indeed, to be forced to undergo a number of cumbersome processes just to be able to manipulate rows and columns separately from one another.
The steps involved in modifying a single column (or row) can be summarized as the following. In the picture below, you will see that in order to make changes to a single column, we need to express the table as a sum of two sub-tables and then make sure to update only one of them.
Algebraically, this kind of procedure can be formulated in the manner shown below. Here, it says that we must perform 3 matrix multiplications as well as an addition, just to record the sum of the frogs' energy numbers in the "score" slot.
Therefore, it is now time to invent some kind of shortcut to let us do things more efficiently. We will go over this topic in the next article.
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service