Linear Algebra for Game Development - Part 15

Author: Youngjin Kang Date: September 30, 2025

Before You Read

This article is Part 15 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.

Scoring and Winning

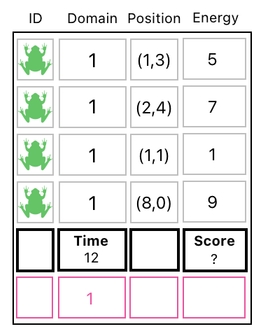
Okay. Now that we have a special row in our data table which is dedicated to storing global numbers, it is now time to talk about one of the most important mechanics in the context of gameplay - winning.

In most cases, people play games in order to win. So it makes sense to assume that a game needs to have a winning condition which, as soon as it is satisfied, allows the player to win.

To decide at which moment the player is supposed to win, we must first come up with a way of measuring the degree of success that the player has achieved so far during gameplay. To fulfill such a purpose, let us create a global number called "score".

Linear Algebra for Game Development - Part 15 (Figure 1)

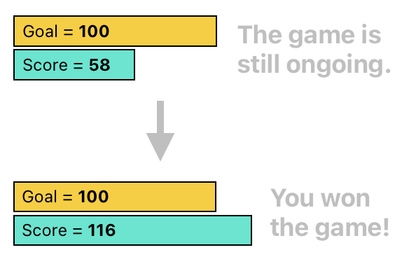
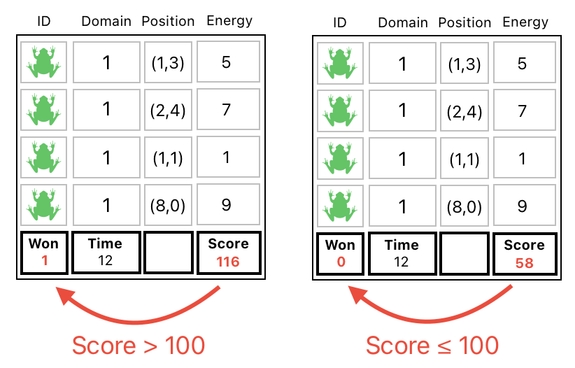
The rule is clear. You win this game when the score surpasses (i.e. becomes greater than) the goal. Let's say that this goal is 100.

Linear Algebra for Game Development - Part 15 (Figure 2)

Besides the score, we need another global property called "won" which explicitly states whether the player has won the game or not. This way, we will be able to tell at which moment we ought to stop playing and congratulate the winner.

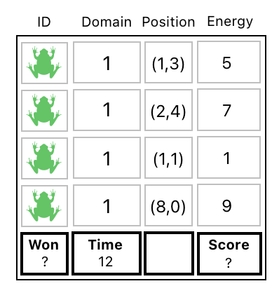
Linear Algebra for Game Development - Part 15 (Figure 3)

The following question, though, is: "What kind of value should be assigned to this 'won' slot?"

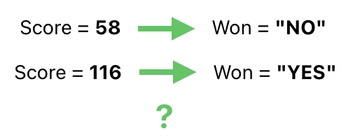
From a conceptual point of view, it might be sensible to simply set the value of "won" to either "YES" or "NO" (or any other pair of English words that are easy to understand), so as to make it crystal clear whether the game is won or not.

From a technical perspective, however, letting numbers and words coexist inside the same table usually turns out to be a hindrance to the consistency of logic. In our case, for example, using "YES" and "NO" as potential values of "won" necessitates us to translate the score (which is a number) to something that is not a number (i.e. a word in English).

Linear Algebra for Game Development - Part 15 (Figure 4)

While it is possible to write an algorithm which accomplishes such a job, we should also be aware that it requires us to introduce an arbitrary set of rules (e.g. if-then statements) which unnecessarily complicates the way we compute things.

A more elegant approach is to use a number to represent the value of "won". This should work, since we can simply let 0 stand for "NO", and anything other than 0 stand for "YES".

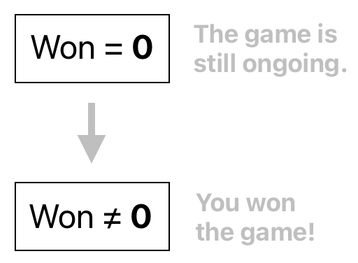
Linear Algebra for Game Development - Part 15 (Figure 5)

In this model, all we have to do to determine the value of "won" is to set the value of "won" to a nonzero number if the score is greater than 100, or zero otherwise.

Linear Algebra for Game Development - Part 15 (Figure 6)

Logic via Arithmetic

The question is, how?

Here, I will show you a hacky little trick which can be used to solve the aforementioned problem without even introducing a new mathematical operator. Take a look at the following expression:

Linear Algebra for Game Development - Part 15 (Figure 7)

Do you remember that the outcome of the "MAX" function is simply the greatest of its arguments (which, in this particular case, are "0" and "Score-100" respectively)? With this in mind, please examine the formula I've shown here and see what it does.

And, yes. You probably guessed it right. The output depends on whether the score is greater than 100 or not.

Linear Algebra for Game Development - Part 15 (Figure 8)

If it is greater than 100, the value of "Score-100" will be greater than 0, which will in turn suggest that the output of MAX will be equal to "Score-100" (since we know that the maximum number between 0 and "Score-100" will always be "Score-100" under such a circumstance). This is a positive number because "Score-100" is positive.

If "Score" is less than or equal to 100, the value of "Score-100" will be less than or equal to 0, meaning that the output of MAX shall be 0 (due to the fact that the maximum number between 0 and "Score-100" will always be 0 under such a circumstance).

Makes sense so far, doesn't it? A major difficulty, though, is that applying this MAX formula to the correct data entries may be tricky.

Luckily, however, we do have a way to mitigate such a trouble. As you may recall from Part 13 of the series, it is technically possible to do some nonlinear, function-based computations using a matrix. Take a look at the augmented table below, where I attached an extra column with the formula "MAX(0,_-100)" in it.

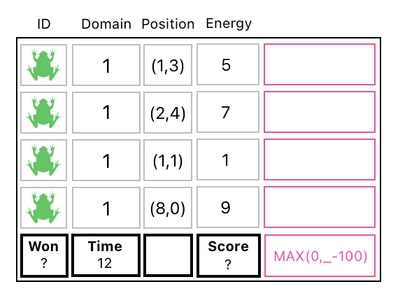
Linear Algebra for Game Development - Part 15 (Figure 9)

What we want to do with this can be described as the following.

(Step 1) First, we want to put the game's current score into the tiny placeholder ("_") which is sitting inside "MAX(0,_-100)", thereby making it "MAX(0,Score-100)".

(Step 2) Next, we want to put the result of computing "MAX(0,Score-100)" into the "won" slot of the table, so as to make sure that the value of "won" will be set to a nonzero number if the score is greater than 100 (or zero otherwise).

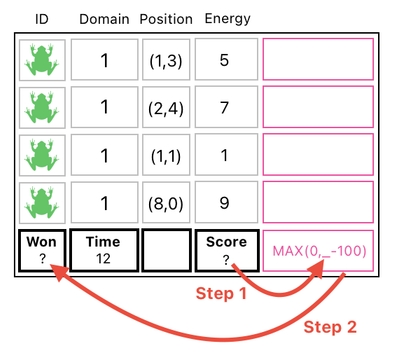
Linear Algebra for Game Development - Part 15 (Figure 10)

And the way we carry out the first step, as illustrated in Part 13, is to add the score to "MAX(0,_-100)". As long as we all implicitly agree that "_" is assumed to be the value of the other term which is being added. This should yield the desired outcome.

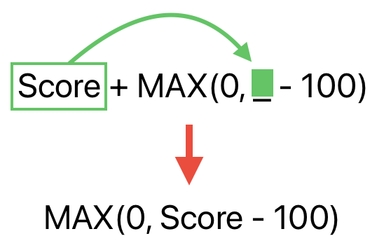
Linear Algebra for Game Development - Part 15 (Figure 11)

Divide and Conquer

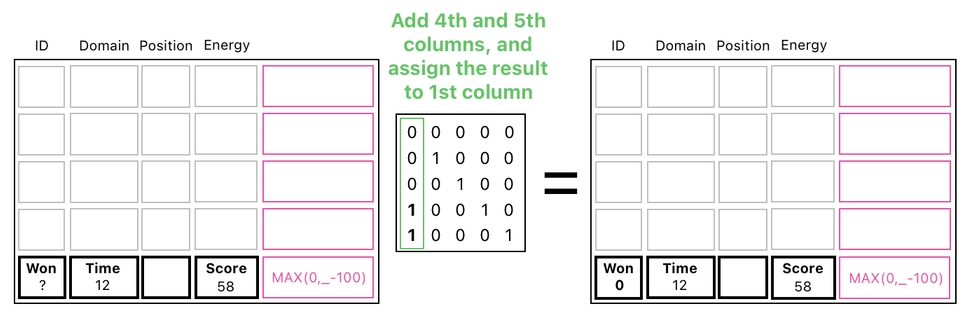
Here is yet another thing which ought not to be overlooked. When it comes to implementing the aforementioned addition, we might be tempted to simply do a matrix multiplication like this:

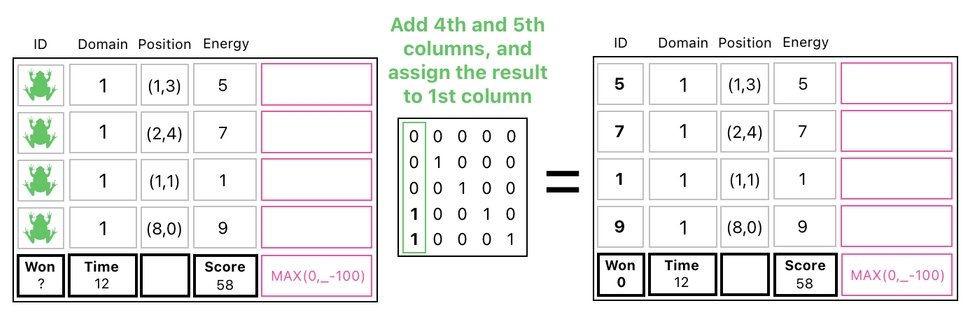
Linear Algebra for Game Development - Part 15 (Figure 12)

Its job is fairly straightforward; we just add the score's column and the MAX formula's column together and assign the resulting column to the one where the "won" value is located. This, without a doubt, yields the correct value of "won" based on the current score.

While doing this, however, it also inadvertently replaced the IDs of the frogs with their respective energy values. The reason is obvious; whenever we are adding a column, we are adding ALL of its entries in parallel!

Luckily, we already know a solution. If you recall the "splitting" method which was demonstrated in Part 5, you will notice that we can just split our table into smaller pieces and process them individually to bypass such an obstacle.

So, let us first divide our table into two segments, okay? The first segment will only contain the four frogs and their properties, which we are able to obtain by erasing the last row.

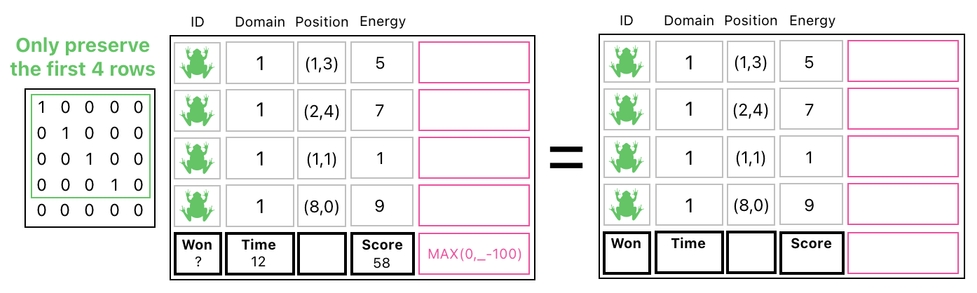
Linear Algebra for Game Development - Part 15 (Figure 13)

The second segment, on the other hand, will only contain the last row (where global properties reside), which we are able to obtain by erasing the first four rows.

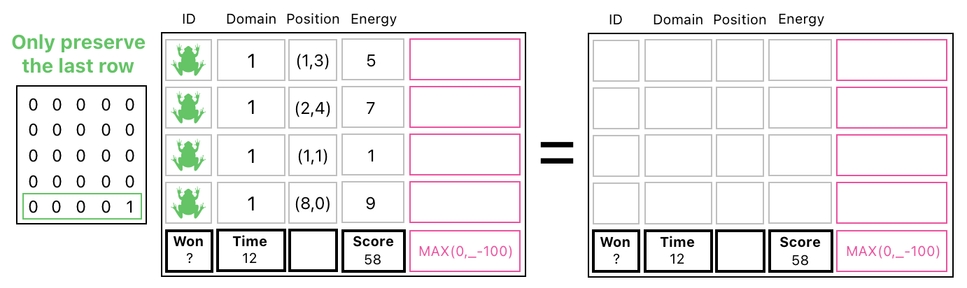
Linear Algebra for Game Development - Part 15 (Figure 14)

We can then safely compute the "won" value of our game by simply adding columns in the second segment (See the picture below). I say it is "safe" because there's no frog that can be interfered with.

Linear Algebra for Game Development - Part 15 (Figure 15)

After recording this new "won" value, all we need to do is bring the two segments back together so as to reconstruct the full table. And the way we do this is by simply adding these two segments up, on an element-by-element basis.

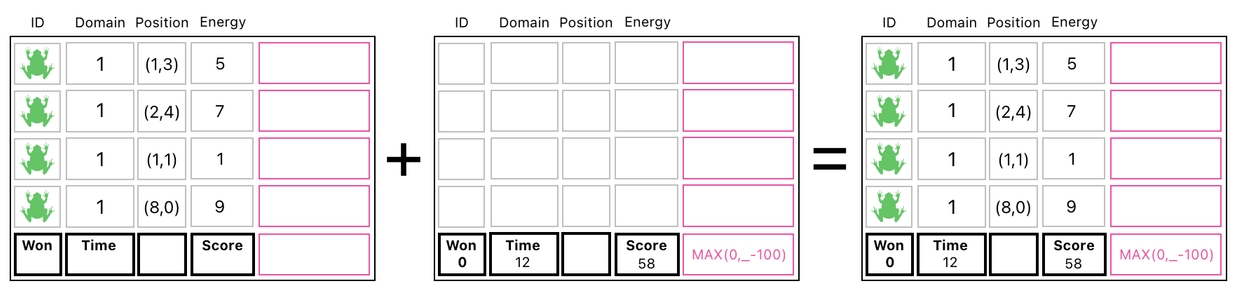
Linear Algebra for Game Development - Part 15 (Figure 16)

The right side of the equation, which you can see in the picture above, is our desired result. The "won" value was successfully set to 0 (which means "You haven't won yet"), since the score is less than or equal to 100. If the score were greater than 100, the "won" value would've ended up being a positive number.

Anyways, the point I want to make is that it is possible to keep track of the game's state by means of adding and multiplying the table's entries. Think of it as some kind of office work involving spreadsheets, wherein you would often find yourself writing a function which reads values from a set of cells, processes them, and assigns the result to another cell.

And the truth is that the whole game might be represented as one big spreadsheet, in which you can establish the rules of play by writing such functions.