Linear Algebra for Game Development - Part 14

Author: Youngjin Kang Date: September 26, 2025

Before You Read

This article is Part 14 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.

Linear and Nonlinear Processes

What we just saw in the previous article is an example of collaboration between two types of processes - one of them being linear, and the other one being nonlinear.

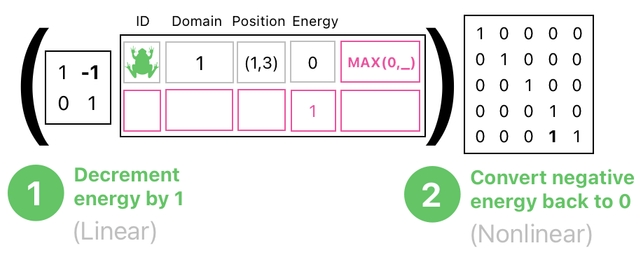
Linear Algebra for Game Development - Part 14 (Figure 1)

In our frog example, there is 1 linear process and 1 nonlinear process.

The job of the linear process is to decrease the frog's energy level by 1, thereby simulating the effect of the frog's periodic consumption of energy (An animal must keep burning its body's fuel to stay alive, you know).

The job of the nonlinear process, on the other hand, is to "filter out" erroneous energy values (i.e. negative numbers) by turning them back to 0. This way, we are able to guarantee that the frog's energy level will make sense no matter how many times the system tries to decrement it.

Two-Step Cycle

In a away, therefore, we are able to imagine our gameplay system as a cycle of two alternating steps - one being linear, and the other one being nonlinear.

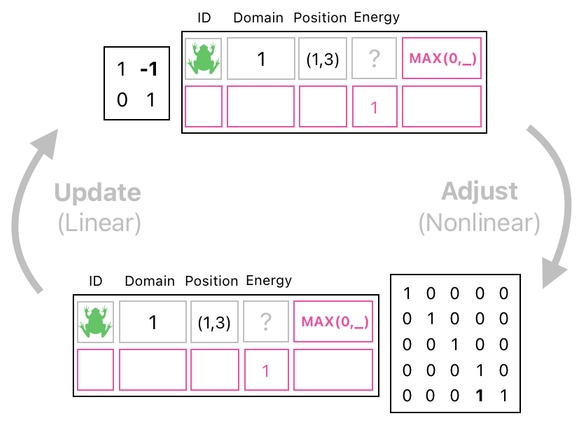
Linear Algebra for Game Development - Part 14 (Figure 2)

During the linear step, we simply update the entries in our table by means of plain old matrices - that is, those involving numbers only, without any strange nonlinear operations such as the "MAX" function we saw before.

Right after doing this, we subsequently wrap up our results by conditionally adjusting them. This is something which should be done by a nonlinear step.

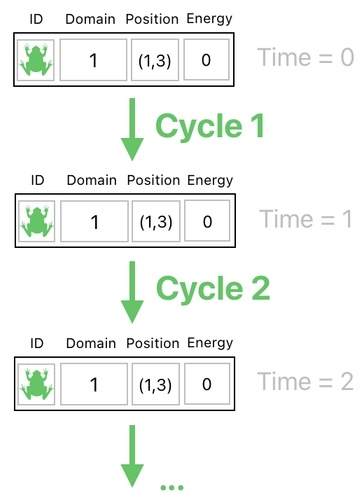
And for the sake of not only updating our data entries but also ensuring their sanity at all times, we must keep repeatedly executing the two aforementioned steps in an alternating manner. That is, once we update the table, we should then adjust it, and then update it again, and adjust it once more, and so forth.

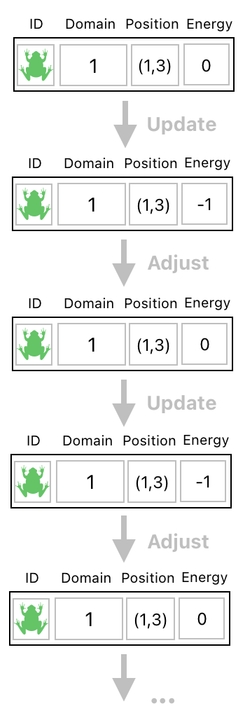
Linear Algebra for Game Development - Part 14 (Figure 3)

As you may have guessed already, the underlying pattern here is that each pair of the two alternating steps (i.e. "update" and "adjust") represents each cycle in the system's clock.

Each time we update our data table and then subsequently adjust its values, a cycle completes itself and the game's clock ticks once. And every time the clock ticks, we increment our current time by 1 (assuming that time is a sequence of discrete units, each of which is quantified by the value of 1).

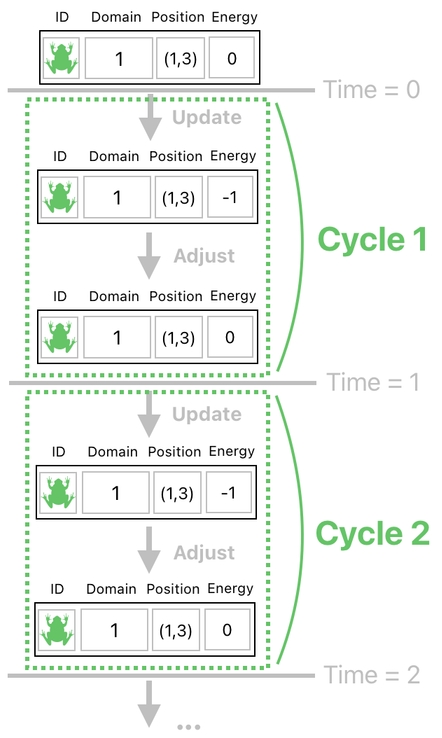
Linear Algebra for Game Development - Part 14 (Figure 4)

Note that each cycle contains two instances of the game's state (aka "snapshots"). Let us take a look at them individually.

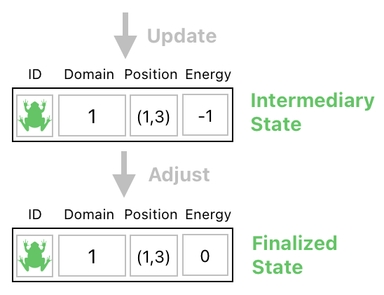
Linear Algebra for Game Development - Part 14 (Figure 5)

The upper one is the immediate result of the crude update process, which is purely linear and thus have none of the necessary adjustments applied yet. The lower one, one the other hand, is the finalized (i.e. adjusted) version of it.

Since the upper one is just an intermediate byproduct, we may as well just ignore it in the context of gameplay and only take the lower one as what is really happening in our game.

Linear Algebra for Game Development - Part 14 (Figure 6)

The philosophy behind this two-step logic is quite clear; it is the decoupling between parts of the system which are linear, and parts of the system which are nonlinear.

Parts that are linear can easily be combined into a linear operator (such as a matrix multiplication), without forcing the developer to worry about violating the rules of linear algebra.

Meanwhile, parts that are nonlinear will have the privilege to be playing in their own playground without hurting the ego of mathematical fundamentalists whose highest achievement in life is that they have memorized every axiom in linear algebra and learned how to apply it without any exception.

Global Properties

Speaking of gameplay cycles and their implication of the concept of time, I would like to mention one major thing which has hitherto been missing. It is the implementation of the universal quantity called "time", which exists independently of any individual objects in our game.

Take a look at the picture below.

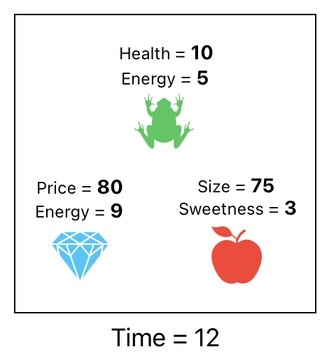
Linear Algebra for Game Development - Part 14 (Figure 7)

Here are 3 objects - a frog, a diamond, and an apple. Each of them possesses its own set of properties, such as energy, health, price, and so forth. Such properties describe the characteristics of these individual objects.

However, there could also be a property which exists independently, such as time.

Time does not belong anywhere; it is a number which is directly associated with the universe as a whole. Whenever we discuss anything related to time, we do not say, "My frog's time is 2:00PM". Instead, we simply say, "The time is 2:00PM" because time is a global property rather than something that is local to any specific object.

The question is, how to represent such an omnipresent being within the context of our data table?

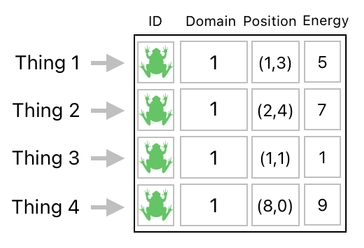
Linear Algebra for Game Development - Part 14 (Figure 8)

As you can tell from the image above, each row typically represents a "thing" in our game, such as a character, an item, or a prop. Therefore, it wouldn't really make sense to record the current time in one of such rows.

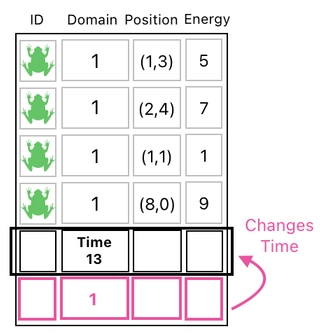
This kind of formulation, however, is not strictly necessary. We may just come up with a special row which will serve as the game's "global record" - that is, a list of data entries which are representative of the game as a whole, rather than mere portions of it.

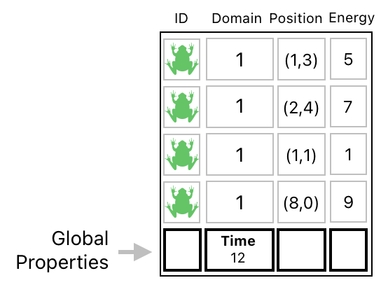
Linear Algebra for Game Development - Part 14 (Figure 9)

Here, for example, I justed added a new row and declared that its second column value indicates the universe's current time (which is apparently "12" right now).

Normally, numbers listed on the second column would all refer to domains to which the game's objects (e.g. frogs) belong. In our example, however, we are designating separate labels to the columns of our "universal row", which make it somewhat special and thus behave differently from any of the other rows.

Time

How to let our time flow, then? That is, how to ensure that the clock is ticking, so that our time will periodically increase, from 12 to 13, from 13 to 14, from 14 to 15, and so on?

Linear Algebra for Game Development - Part 14 (Figure 10)

To achieve such an objective, we need some way of adding 1 to the current time. And you what? For this particular purpose, we can just reuse the same "domain building block" we used before, when we were killing/reviving the frogs. Here, I will include this particular building block at the bottom of the data table (See the picture below).

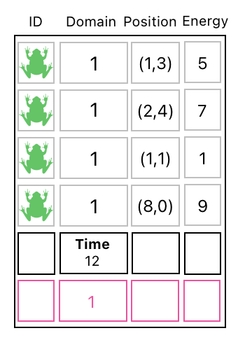
Linear Algebra for Game Development - Part 14 (Figure 11)

The role of the bottommost row here depends on its usage.

Whenever we add it to one of the "frog rows" (in which case it will be transforming the frog's domain value), it will play the role of a "domain building block".

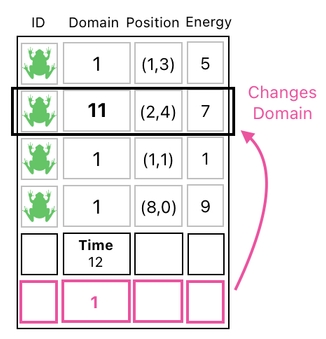
Linear Algebra for Game Development - Part 14 (Figure 12)

Whenever we add it to our "universal row" (in which case it will be transforming the universe's time value), on the other hand, it will play the role of a "time building block".

Linear Algebra for Game Development - Part 14 (Figure 13)

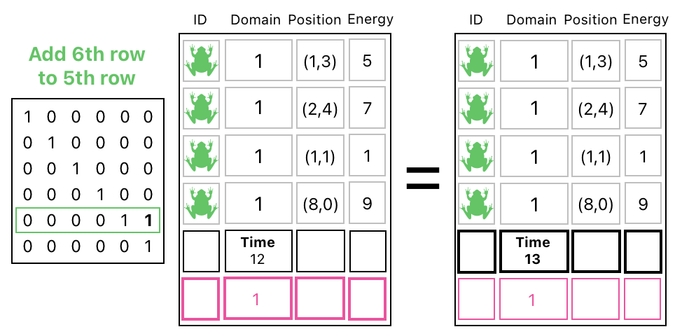
Here is an idea. By accumulating this "time building block" in a periodic manner, we are able to simulate the passage in time. And the way we do this is not so different from what we have been doing so far with the so-called building blocks; we just add them to the rows we want.

We know that, in our case, the goal is to periodically increment the time by 1. This can be done by adding the "time building block" to the row of global properties, wherein the time value resides.

Linear Algebra for Game Development - Part 14 (Figure 14)

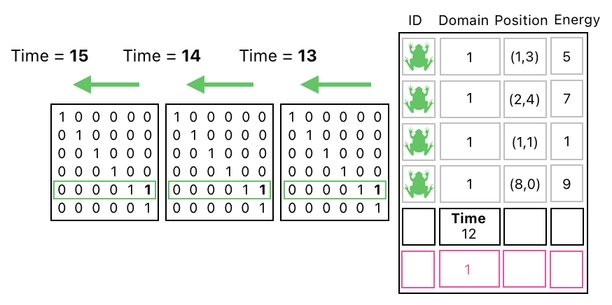
As you can see, this operation is equivalent to the act of ticking the clock. Every time we multiply our table by the matrix shown above, we tick the clock (i.e. increment the time by 1). And we need do this over and over at regular intervals. This will keep the time flowing.

Linear Algebra for Game Development - Part 14 (Figure 15)