
Author: Youngjin Kang Date: November 11, 2025
This article is Part 23 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
We have seen quite a number of examples so far, in the context of gameplay mechanics. We have seen how game characters are able to interact with one another by means of search protocols such as target-finding, collision detection, etc.
The ultimate roots of such interactions are what we typically refer to as "relations".
The world is made up of things, and things are related to each other. If things weren't related to each other, no interaction would exist because everything would end up being a completely isolated singleton - a self-enclosed universe of its own.
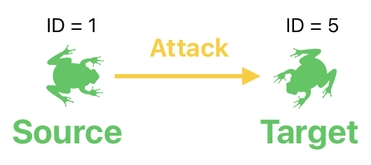
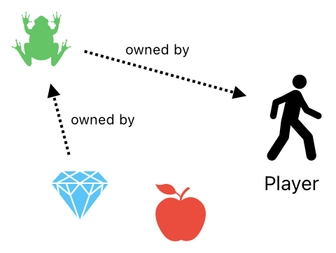
When a frog attacks another frog, we say that there is a relation called "attack" which involves one of them as the source, and the other one as the target.
When a pair of circles collide, we say that there is a relation called "collision" which involves both of them, each of which is trying to push its opponent away by means of a mechanical force.
Another example can be found in the concept of "inventory", which I introduced during the early part of this series. Inside a video game, we usually expect the player to have its own inventory, in which items can be stored and carried around.
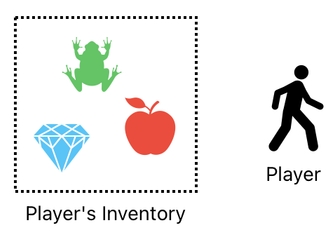
This, too, is an example of a relation. Each item in the inventory is "related" to the player in the sense that the player owns it. In other words, we can suppose that there is a relation called "ownership" which is made up of two constituents - the owner (i.e. player) and the thing that the owner owns (i.e. player's item).
If there are 3 items in the player's inventory, therefore, we may as well claim that there are 3 instances of the "ownership" relation between these 3 items and their owner (i.e. player).
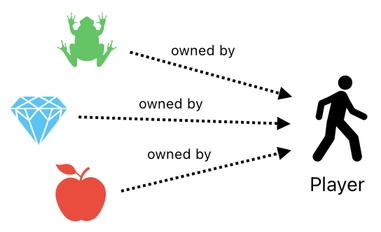
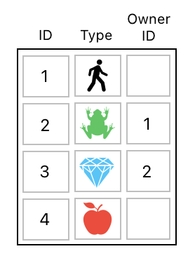
Such a relation can be modeled as a column in our data table, like the one shown below:
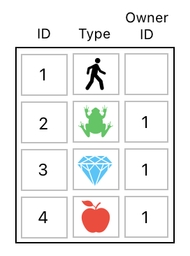
Here, the column labeled "Owner ID" is used for storing the ID of each item's owner. Since all 3 of the items (i.e. frog, diamond, and apple) are owned by the player in our example, their owner IDs are all set to the player's ID (which is 1). The owner ID of the player itself is empty (0), since the player itself is not owned by anybody.
What happens when the player no longer owns the apple?
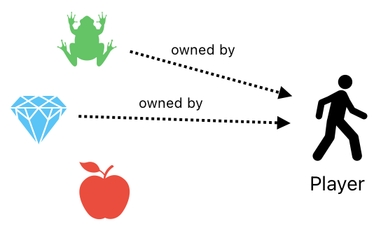
In this case, the apple's owner ID will be empty (0) as well because it is no longer owned by anyone.
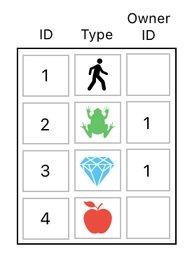
Now, here is another twist. What if the diamond is no longer owned by the player directly, but is owned by the frog, which is in turn owned by the player?
Oh, it's simple. The diamond's owner ID should be set to the frog's ID (which is 2) because it is now owned by the frog.
As we can see in these short examples, relations can be modeled in terms of references.
A "thing" can make a reference to another thing by means of an identifier, such as the ID of a row. And wherever there is a reference, it can be stated that there must be SOME relation between the thing that is being referenced, and the thing that is referencing it.
Depending on what kind of gameplay mechanic we are looking for, though, there might be an issue of inconvenience with regard to the handling of multiple items. To demonstrate what I mean by this, I will revisit the earlier example in which all 3 of the items (i.e. frog, diamond, apple) are owned by the player,

which can be expressed by the following table.

Here, what we are witnessing is the fact that we have to set the "owner ID" of all 3 of the items to the player's ID (which is 1), in order to be able to state that they are all owned by the player.
This is hardly a hassle, but imagine a scenario in which the player happens to be carrying hundreds of items in the inventory. Do we really have to assign the player's ID to every single one of their "owner ID" slots, in order to express the idea that the player owns them all? I think not.
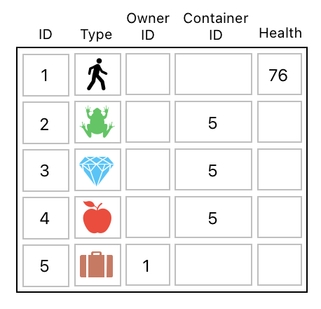
Fortunately, there is a much more elegant way of handling ownership. First, think of the player's inventory as an item of its own, which occupies a row in the data table (just like the frog, diamond, and the apple).

Then, instead of allowing the frog, diamond, and apple to be directly owned by the player, let us define them as things that are "contained" inside the player's inventory, whereas the inventory itself is owned by the player.
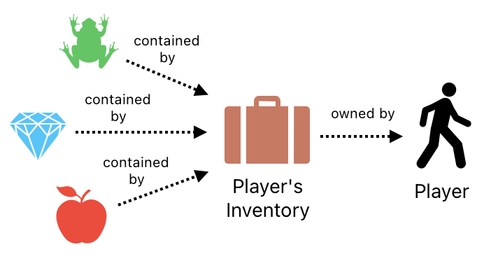
In table form, this can be modeled as the following.
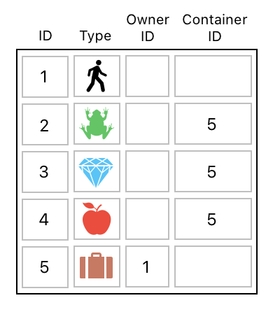
Do you see the new column called "container ID"? The use of this is to indicate which items are contained by which. By looking at it, you will be able to tell that the frog, diamond, and apple are contained in the inventory (which is denoted by the brown suitcase), while the inventory itself is owned by the player.
The practical implication of this is pretty self-explanatory. By modeling the player's inventory as a separate item and making it a container which holds all the items that the player owns, we are able to group multiple items together under the authority of a single entity. This lets us handle all of them at once, instead of having to deal with them individually.
The major advantage of this new approach will be evident once you see the example below.
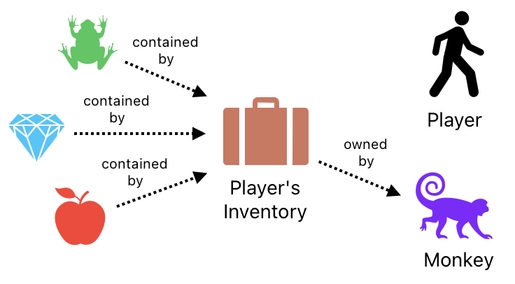
Here, I just changed the owner of the 3 items (i.e. frog, diamond, apple) from the player to a monkey (Let's say that the monkey stole the suitcase from the player or something).
How shall we represent this sort of situation? If we were to stick to our original method, we would have to modify the "owner ID" of every one of the 3 items in order to declare that their owner has changed. In our new method, on the other hand, all we need to do is simply change the "owner ID" of the inventory to the monkey's ID.

Since the frog, diamond, and apple are all part of the inventory, changing the owner of the inventory alone will be sufficient to ensure a change in the owner of every one of them.
What we have seen so far is nothing more than the tip of the iceberg. One thing I want to emphasize is that pretty much ANY part of gameplay can be considered a relation. And this includes some of the most fundamental building blocks of game design such as state variables (e.g. stats).
Imagine, for example, that besides owning an inventory of 3 items (i.e. frog, diamond, apple), the player also carries a health bar.
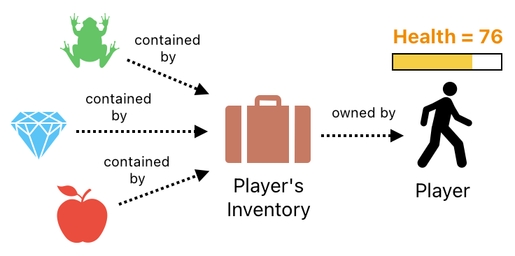
Let us say that, according to the health bar, the player's current health is 76. How shall we express this fact?
Oh, for sure, we can add an additional column called "health" to our data table, and fill its entry in the player's row with the number 76. This will clearly indicate that the player's health is 76.
Here is something important to keep in mind. From a mathematical point of view, there is no fundamental difference between the player's health and what we've hitherto been referring to as "relations". That is, it is perfectly valid to say that "health" is just another type of relation.
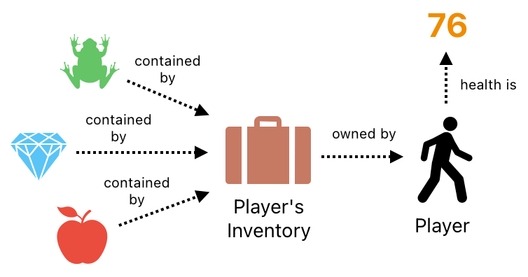
Just like the 3 items (i.e. frog, diamond, apple) are related to the inventory by the "contain" relation and the inventory itself is related to the player by the "own" relation, we can claim that the player is related to the number 76 by the "health" relation.
Previous Page Next Page
© 2019-2025 ThingsPool. All rights reserved.
Privacy Policy Terms of Service