
Author: Youngjin Kang Date: September 18, 2025
This article is Part 12 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
Let me revisit the methodology I just introduced recently. As you may remember, it is possible to kill (i.e. send to Heaven) all of the frogs in our gameplay universe by simply adding to them multiples of the "domain building block", which is just an extra row attached to the data table.
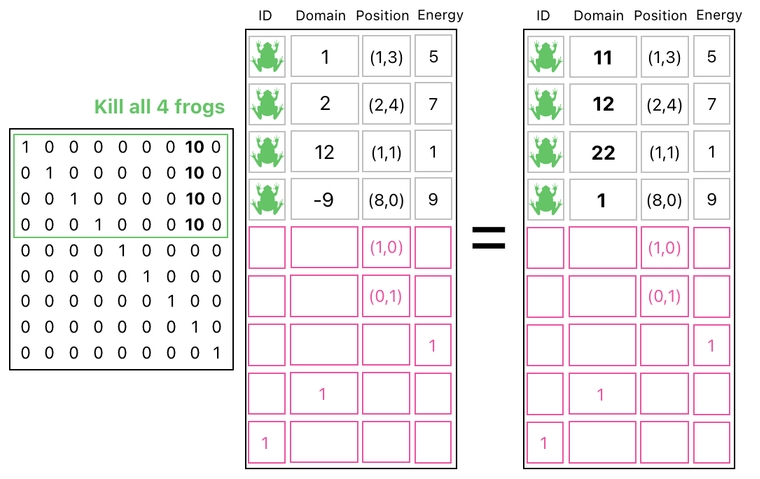
In the picture above, for instance, I am multiplying the 8th row of the table by 10 and adding it to every frog-occupied row. This has the effect of adding 10 to every frog's domain value.
There is something which bugs us, though. As you can see in the matrix, we are responsible for filling out 4 entries with number 10 to be able to kill 4 frogs. This seems like a trivial matter, but imagine that there are 1000 frogs in total, and that we are trying to kill all of them at once. This means that we will have to fill out 1000 entries in the matrix, which is too much work to do.
Fortunately, there is a nice shortcut.
In order to to explain how this shortcut works, let me first mention that all of the so-called "building blocks" we have been dealing with are rows, instead of columns.
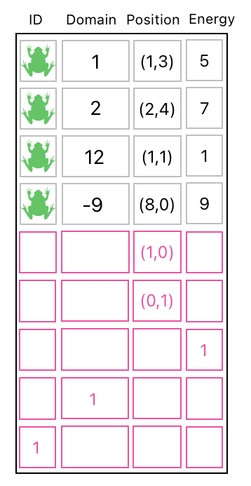
Here, we are seeing 5 distinct building blocks out of which a frog can be made - one for the frog's X-position (5th row), one for the frog's Y-position (6th row), one for the frog's energy (7th row), one for the frog's domain (8th row), and one for the frog's ID (9th row).
Building blocks, however, are not required to be in the form of rows. We may as well devise them as columns, which in some circumstances is more appropriate than having them as rows. And I will show you why.
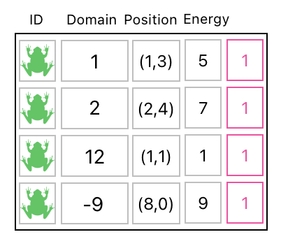
Take a look at the table above. Do you see an extra column, filled with all 1s? We can interpret it as a building block, too. In this particular case, it represents a building block of what we could refer to as "uniform change" - an act of shifting the values of an entire column by a fixed amount.
It turns out that, by means of a matrix multiplication on the right side (since we are dealing with columns instead of rows), it is possible to scale this extra column by the factor of 10 and add it to the "domain" column of the data table. This yields a uniform shift in the domain value of every row by 10.
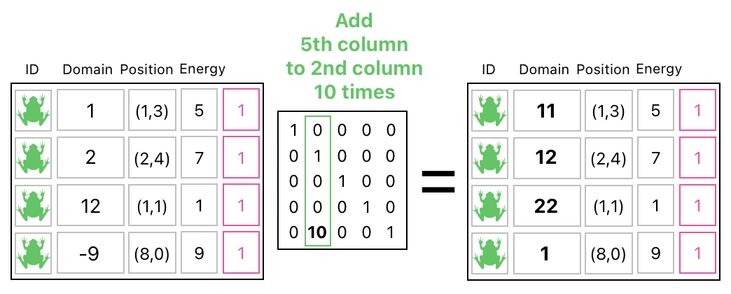
And of course, we know the meaning of such a transformation. It indicates a simultaneous death of every frog in the universe.
The same exact building block can be used for the periodic decay of energy in every frog. Let me come up with an example for the purpose of demonstration.
As common sense tell us, animals must keep spending energy in order to stay alive, and frogs are not an exception. An accurate simulation of our real world would be one which reflects such a concept.
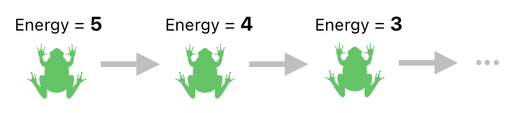
And the way in which we can implement it turns out to be simple as long as we just leverage the extra column we added. Just scale it by -1 and add it to the "energy" column of the data table, and you will see that the energy of every single frog will decrease by 1.
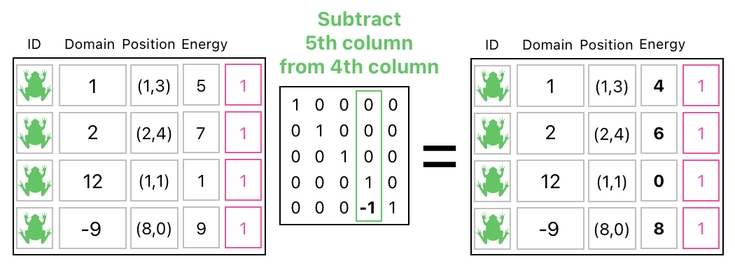
We can carry out such an operation over and over on a periodic basis. This way, we will be able to let every frog consume a single unit (= 1) of its stored energy each time the clock ticks.
What if we wish to drain the energy at half the rate, though? That is, what if our intention is to drop each frog's energy by 0.5 instead of 1 at each step in time (on average)?
One may say that we must be able to achieve it by subtracting only half (= 0.5) of the rightmost column from our "energy" column, but let us assume that energy can only be an integer (due to each unit quantity (= 1) being an indivisible energy particle).
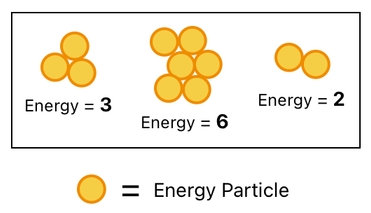
In such a case, we are unable to subtract only a fraction of a unit of energy and thus have to look for another solution.
Fortunately, there is one neat way in which we can produce the effect of reducing each frog's energy at half the rate. It works by dividing our frogs into two groups, and decreasing the energy levels of only one group at a time (in an alternating manner).
In order to do that, let us create two separate columns in our data table. The first one (5th column) is filled with [1 0 1 0...], whereas the second one (6th column) is filled with [0 1 0 1...].
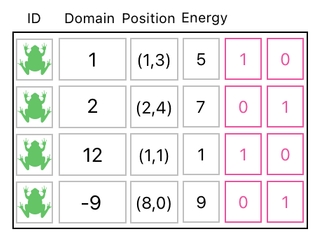
Notice the two opposing patterns here? Both of them are sequences of alternating 1s and 0s, yet the initial values at which they begin differ. One of them starts at 1, while the other starts at 0.
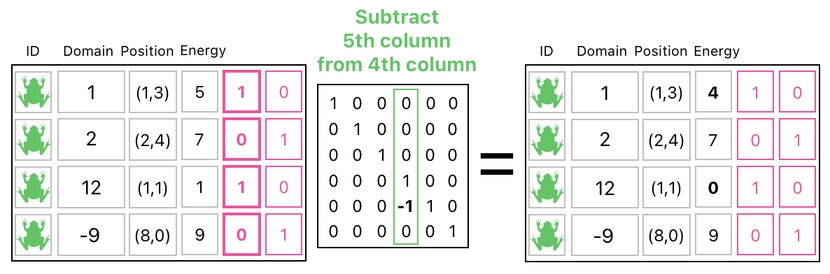
If we subtract the 5th column from the "energy" column, only the 1st and 3rd rows (i.e. frogs) will have their energy values dropped by 1. You can see how it works by looking at the formula below.
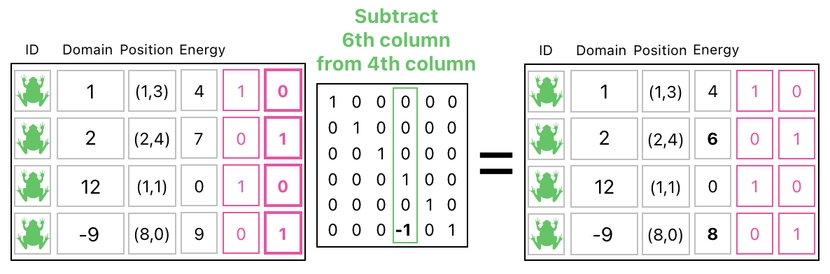
If we subtract the 6th column from the "energy" column, on the other hand, only the 2nd and 4th rows (i.e. frogs) will have their energy values dropped by 1. It is because all the 1s and 0s are flipped in this case.
Now, what is going to happen if we periodically carry out the two operations above in an alternating manner? That is, what sort of effect do we anticipate when we subtract the "energy" column by the 5th column, and then by the 6th column, and then by the 5th column, and then by the 6th column, and so on?
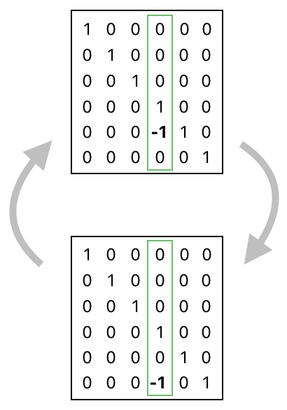
The obvious efect we are bound to see is that of a train of alternating changes which, on average, reduces every frog's energy by 1 per each interval of 2 time steps (aka "2 matrix multiplications"), which means that the overall rate of energy reduction is 0.5 (= 1/2) per time step.
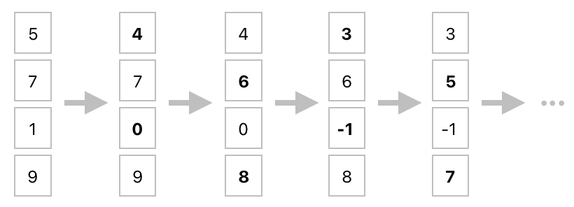
Let me now come up with something slightly more complex. Imagine that there are 4 frogs in the world, and that one of them killed the other ones by spending 4 energy points.
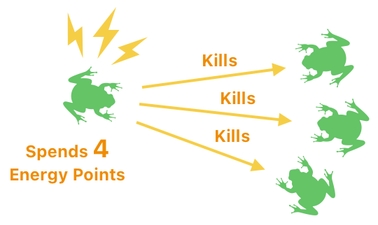
This is such a typical gameplay scenario, right? A game character spending energy to kill its enemies (which in this, are the other 3 frogs) is, as you know, an all too common thing which recurs continually while playing a game. Oftentimes, one feels that it is a good idea to sacrifice one's resources to be able to fulfill a certain wish - an exchange between an end and its means.
In the aforementioned case of a frog consuming its energy to kill the other frogs, we are able to tell that there are two events happening simultaneously:
(1) The energy of one of the frogs being reduced by 4, and
(2) The other 3 frogs being sent to Heaven (i.e. their domain value being increased by 10).
In what manner shall we invoke these two events at once? For such a purpose, we will need both a row-based building block and a column-based building block, like the ones shown below.
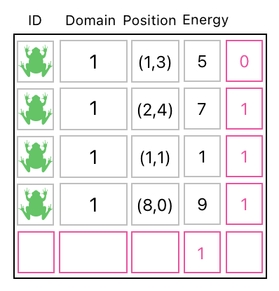
Here, the data table contains both an extra row which can be used for modifying the energy value of any row, as well as an extra column which can be used for modifying the domain values of all the frog-occupied rows except the first one.
Now, what do we need to do whenever we want to fiddle with the table's rows? The answer is, we multiply a matrix on the left side of the table.
And what do we need to do whenever we want to fiddle with the table's columns? The answer is, we multiply a matrix on the right side of the table.
So, now that you are reminded of these two important points, take a look at the arrangement of two matrix multiplications below. You will be able to tell, with a bit of analysis, what these two are doing.
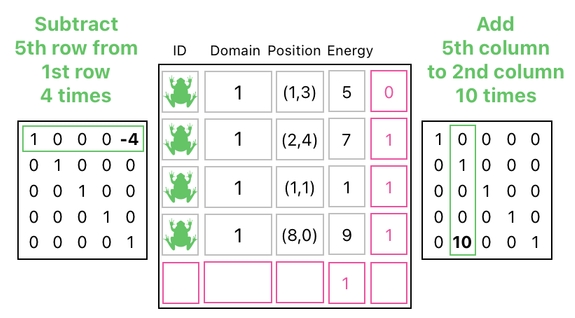
And you probably guessed it right. The matrix on the left subtracted 4 energy points from the first frog, and the matrix on the right added 10 to the domain of every frog except the first one.
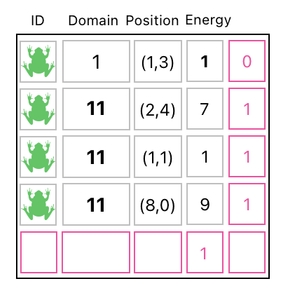
As you can see, it is possible to let our data table have building blocks both on its rows and columns, and use them simultaneously.
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service