Linear Algebra for Game Development - Part 11

Author: Youngjin Kang Date: September 14, 2025

Before You Read

This article is Part 11 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.

Multiple Levels of Heaven

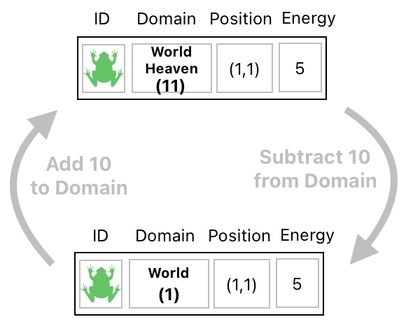
It is now pretty obvious that, by assigning numbers to our domains (e.g. world, inventory, etc), we can simply represent the process of death as the increment of one's domain value by a fixed amount (such as 10), and the process of birth as its inverse (i.e. decrement).

Linear Algebra for Game Development - Part 11 (Figure 1)

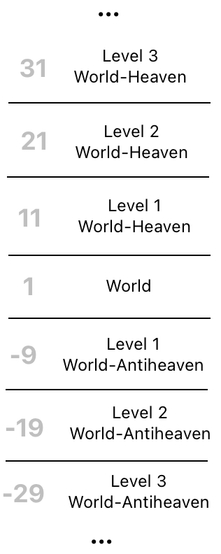
Since both domains and their respective heavens are being expressed numerically, we should be able to imagine them as points on a number line, such as the one illustrated below. Here, the point at "1" indicates the world, whereas the point at "11" indicates the world-heaven.

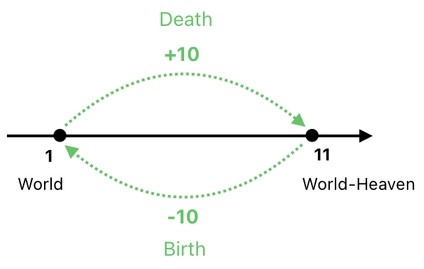
Linear Algebra for Game Development - Part 11 (Figure 2)

When somebody in the world dies, he enters the world-heaven. This is done by adding 10 to his domain value (because the world is located at 1 and the world-heaven is located at 11). If he happen to reincarnate while he is in the world-heaven, we will bring him back to the world by subtracting 10 from his domain value.

And, just like we saw before, there could be multiple domains in Heaven as well as multiple domains on Earth. If we do suppose that 1 and 2 refer to the world and the inventory, respectively, as well as that 11 and 12 refer to their corresponding heavens (i.e. "world-heaven" and "inventory-heaven"), we can plot them as two pairs of points on the number line, such as the one shown here:

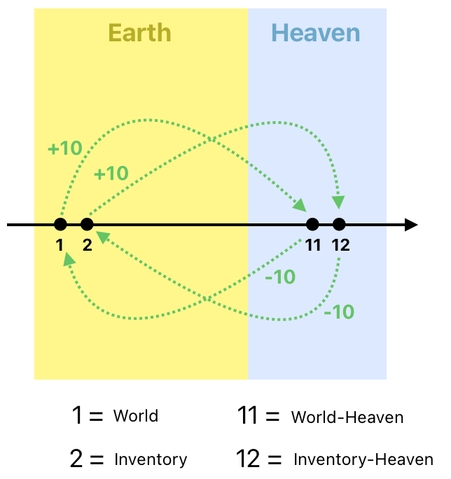
Linear Algebra for Game Development - Part 11 (Figure 3)

In this diagram, you will clearly be able to tell that the number line is divided into two regions.

The points on the left region represent earthly domains which are being dwelled by living creatures, whereas the points on the right region represent heavenly domains which are being dwelled by ghosts.

The act of moving a point to the right by the distance of 10 (aka "adding 10"), then, has the effect of moving the point from Earth to Heaven. In contrast, the act of moving a point to the left by the distance of 10 (aka "subtracting 10") has the effect of moving the point from Heaven to Earth.

Here is a question, though. What happens when we kill something which is already dead (i.e. already in Heaven)? The answer is, it will enter what we could refer to as the "level 2 heaven".

The first time something dies while it is on Earth, it will enter the "level 1 heaven". The next time it dies, it will level-up to the heaven's heaven, which is "level 2 heaven" (Level 0 refers to Earth; it's the "ground level" after all).

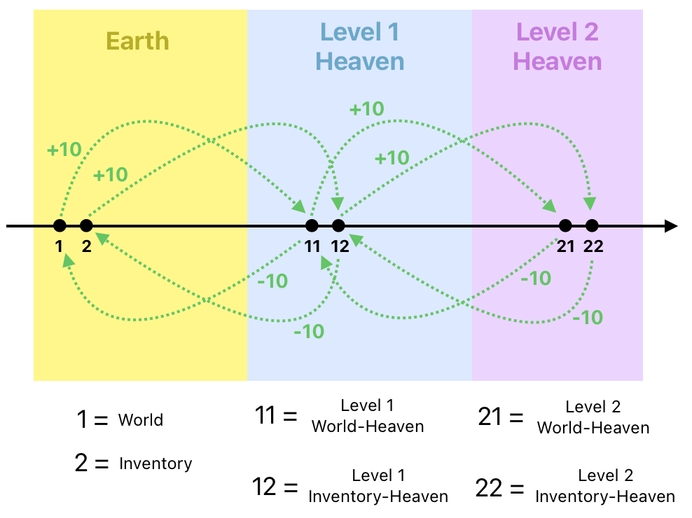
Linear Algebra for Game Development - Part 11 (Figure 4)

And of course, each level itself may comprise multiple domains. At level 0, we have both the world (1) and the inventory (2); these two realms are the ones in which living things reside. At level 1, we have the world-heaven (11) and the inventory-heaven (12). At level 2, we have the world-heaven's heaven (21) as well as the inventory-heaven's heaven (22).

Spectrum of Domains

And you know what? We can extend the aforementioned definition to infinity, so that the act of killing/reviving will make sense no matter what the current value of the domain is.

The truth is that nothing stops us from making things up, since our gameplay universe is purely fictional. With this in mind, let us assume that there are infinite levels of heavens, as well as infinite levels of "antiheavens" which correspond to negative domain values.

Linear Algebra for Game Development - Part 11 (Figure 5)

So, if you happen to "resurrect" while you are still alive, you will enter the level 1 "antiheaven" (instead of heaven) due to the extra layer of life you just acquired. If you get killed while hanging out in this antiheaven, you will be transferred back to the land of living creatures (i.e. Earth).

The general idea, though, is that such an extended definition lets us imagine that there is an infinitely long line of domain values (just like a line of real numbers in mathematics). In this model, we can shift any domain value by 10 however many times we want, and the result will still be a fully legitimate domain value.

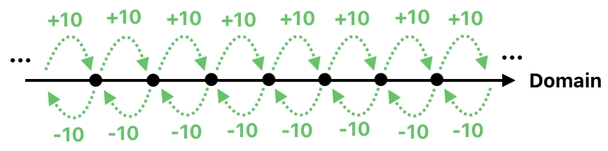
Linear Algebra for Game Development - Part 11 (Figure 6)

This kind of unboundedness allows us to imagine the so-called "domain" as just another dimension in space.

Linear Algebra for Game Development - Part 11 (Figure 7)

In this alternative model, the act of killing somebody is the same as pushing him in the direction of the domain axis by the distance of 10, and the act of reviving somebody is the same as pushing him in the opposite direction by the distance of 10.

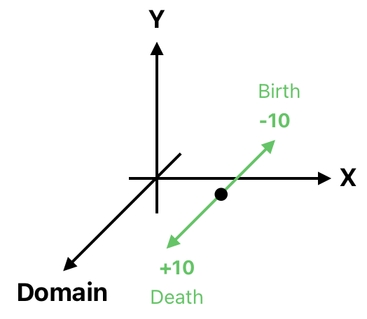
Linear Algebra for Game Development - Part 11 (Figure 8)

Multikill

"Okay, so what's the use of such an abstract model?", you might ask. Here, I will show you a reason why expressing life/death in terms of a spectrum of numbers is so useful.

Suppose that there are 4 frogs in our game, and we want to kill them all by dropping a nuke or something. This sort of event is not so uncommon in a video game, by the way. The player might for example be equipped with a special weapon which, when deployed, will annihilate everything in the known universe.

Linear Algebra for Game Development - Part 11 (Figure 9)

Here is a problem, though. Imagine that the kind of weapon we are about to drop is not just a regular nuke, but some kind of "pandimensional nuke" which is capable of destroying the lives of not just those who are here on Earth, but also those who reside in heavens, antiheavens, and every other supernatural realm we can think of.

So, for example, imagine that each of the 4 frogs in our game exists in a separate domain, and that two of these domains do not even belong to Earth; one of them is a heaven, and the other one is an antiheaven.

Linear Algebra for Game Development - Part 11 (Figure 10)

How, then, are we going to "kill" all of these frogs simultaneously? One of them is already dead (i.e. It is in Heaven), and the other one is anti-dead (i.e. It is in Antiheaven). Will it even make sense to "kill" something which is either already dead or anti-dead?

And the thing is, yes! It absolutely makes sense to kill something regardless of its current state of life/death. The reason is that the process of killing is nothing more than the addition of number 10 to one's domain value.

For the sake of demonstration, let me list the aforementioned 4 frogs as rows in the data table.

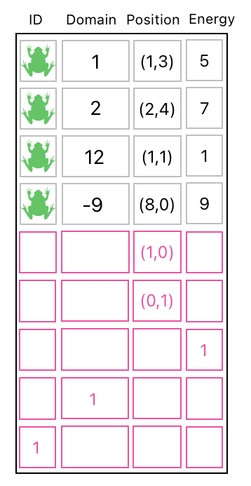
Linear Algebra for Game Development - Part 11 (Figure 11)

As you can see, their domain values are different from each other. The first (topmost) frog belongs to the world, the second frog belongs to the inventory, the third frog belongs to the level 1 inventory-heaven (i.e. This frog is dead), and the fourth frog belongs to the level 1 world-antiheaven (i.e. This frog is anti-head).

The way we kill all these 4 frogs is surprisingly easy from a computational point of view. The only thing we have to do is keep them as they are, while making sure to add 10 to each of their domain values. This can be done by adding 10 copies of the "domain building block" to each of the first 4 rows of the data table.

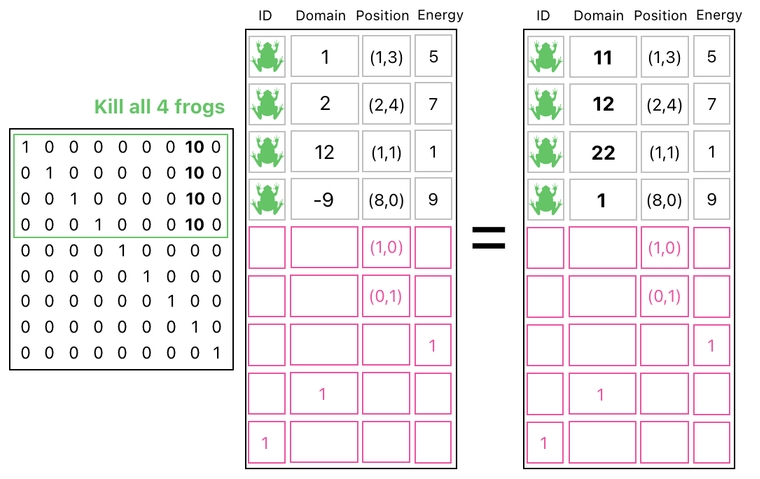
Linear Algebra for Game Development - Part 11 (Figure 12)

And the effect of doing this can be stated as the following:

- The frog in the world (1), after being killed, entered the level 1 world-heaven (11).
- The frog in the inventory (2), after being killed, entered the level 1 inventory-heaven (12).
- The frog in the level 1 inventory-heaven (12), after being killed, entered the level 2 inventory-heaven (22).
- The frog in the level 1 world-antiheaven (-9), after being killed, entered the world (1).

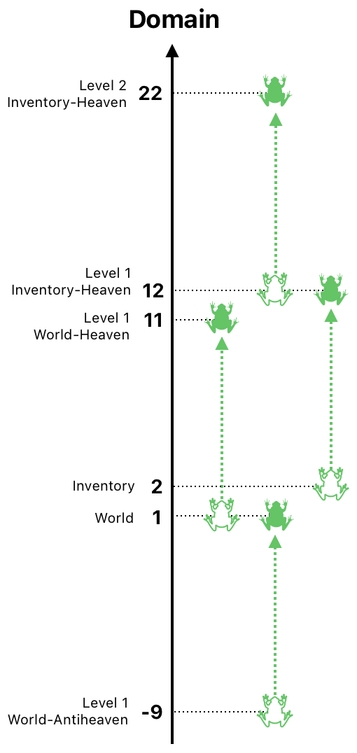
Linear Algebra for Game Development - Part 11 (Figure 13)

What happened here is just a verbose description of the fact that we just "moved" all these 4 frogs by the distance of 10, in the direction of the domain axis.

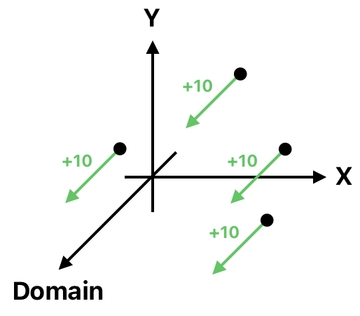
Linear Algebra for Game Development - Part 11 (Figure 14)

And the result of every one of these movements is guaranteed to make sense, since the distance between every domain and its respective heaven (i.e. the place to which the domain-dweller goes when it dies) is always 10.