
Author: Youngjin Kang Date: September 10, 2025
This article is Part 10 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
In the previous article, we saw that it is not so hard to create a new object (such as a frog), introduce it to the world, and then destroy it later on. All we had to do was fill up a row in the data table with some combination of building blocks to spawn something, and then clear out that particular row once we decide to despawn it.
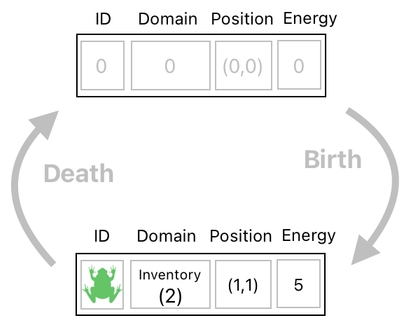
Here is a potential problem, though. When we erase a row (by turning every one of its column values to 0), there is no way to recover its original values, meaning that we are unable to revive something we just killed.
This, of course, makes perfect sense in ordinary life because (unless a miracle happens) a living thing simply cannot come back to life after it dies.
Since a game is a work of fiction, however, it is often fun to grant ourselves a magical power to raise the dead from their graveyard. How shall we implement such a power?
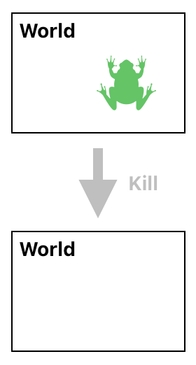
If we want to be able to bring the dead back to life, we must stop completely annihilating something whenever we decide to kill it. To explain the reason why, let me suppose that there is a frog inside the world, like the one shown here.

If we kill this frog by simply erasing it (without making a backup), it will be gone forever! There will be absolutely no way to bring it back to existence, since we won't have access to the piece of information we need ("1 1 5 2 2") to reconstruct the original frog.
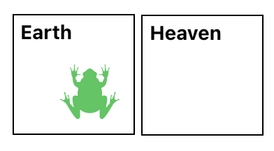
In order for resurrection to be viable, therefore, we need to have some kind of "backup storage" in which we can temporarily store the dead frog, so as to be able to bring it back to life later on. To make room for such a storage, we need to partition the world into two distinct parts - Earth and Heaven.
From now on, when we decide to kill the frog, we will move it over to Heaven instead of just erasing it. Think of Heaven as the frog's backup storage, hosted on the cloud.
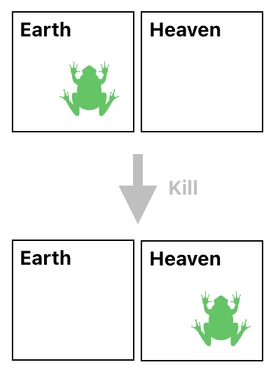
Later on, if we want to resurrect the frog, we will simply need to bring it back to Earth. That way, we will successfully recover the original copy of the frog without having to remember and reconstruct it by ourselves.
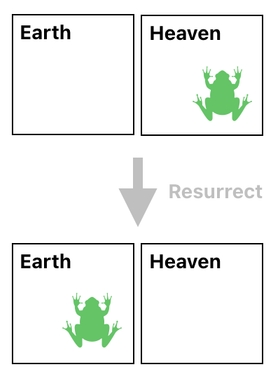
And the way we implement this is easy. All we need to do is change the frog's domain from "Earth" to "Heaven" when it dies, and change it back to "Earth" when it revives.
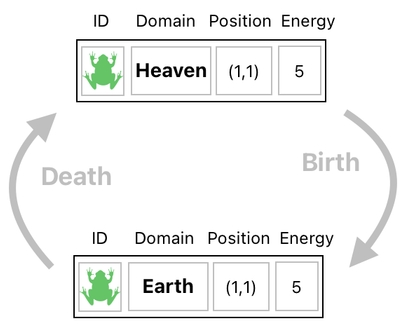
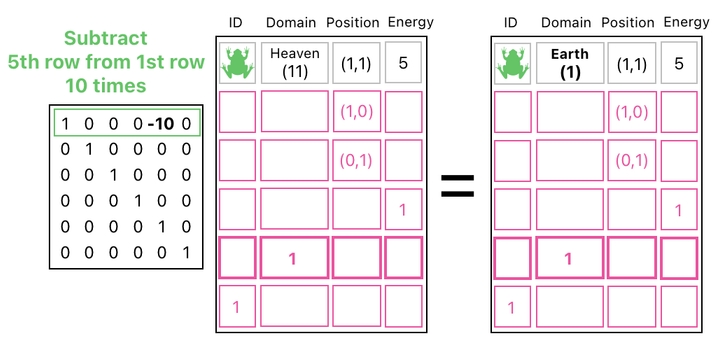
This kind of transformation, indeed, will need to be modeled in terms of numerical operations. For such a purpose, let us begin by assigning numbers to our domains. For example, let's say that Earth is 1 and Heaven is 11.

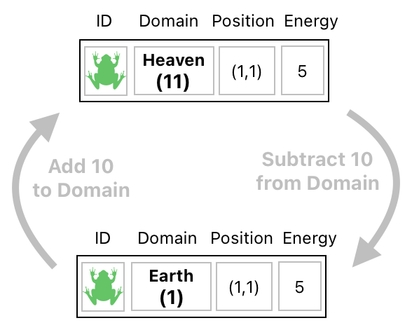
What sort of action, then, will we need to take if we want to kill the frog (i.e. teleport it from Earth to Heaven)? Oh, the answer is crystal clear. Since Earth is 1 and Heaven is 11, we know that adding 10 to Earth will turn it into Heaven. Therefore, if the frog is currently on Earth (1), the only thing we will need to do is increment the domain's value by 10 to change it to Heaven (11).
The opposite scenario is equally straightforward. If the frog is in Heaven (11) and we want to bring it back to Earth (1), all we need to do is decrement the frog's domain by 10.
In the language of matrix multiplication, it is evident that multiplying the domain's building block by 10 and adding it to the frog's row is equivalent to increasing the frog's domain by 10. If the frog is currently on Earth (1), executing such an operation will move it over to Heaven (11). This is how we kill a frog.
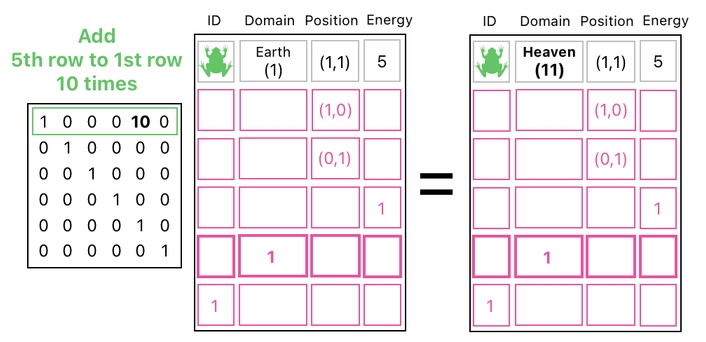
If we multiply the domain's building block by 10 but subtract it from the frog's row instead, the frog's domain will decrease by 10 (instead of increasing). If the frog is currently in Heaven (11), therefore, executing such an operation will move it back to Earth (1). This is how we resurrect a dead frog.
"But, what about the inventory?" you might ask. And in fact, you are absolutely right that the method I just described does not take the idea of inventory into account.
Previously, I had mentioned that it is often necessary to split our game into multiple spatial realms such as "world" and "inventory", where the world refers to some kind of 3D space in which physical interactions happen, whereas the inventory refers to some kind of 2D grid in which items are being stored, and so forth.
A question may arise, then. What is going to happen if a frog in the player's inventory suddenly dies? Will it go to some kind of "inventory-heaven", as opposed to "world-heaven"?
Some people may argue that such a division is unnecessary, yet here is an important point to keep in mind. When a frog in the inventory dies, goes to Heaven, and then comes back to life, at which place will it respawn?
It may be argued that it doesn't really matter, and that the place of resurrection can be wherever we want, but here is an example which will prove that such a claim is groundless. Imagine that a vampire dies and is buried in a coffin. When it comes back to life, at which location shall we expect to see the vampire again? The same exact coffin, of course!
Therefore, if a frog dies in the inventory and comes back to life later on, we should be able to see the resurrected frog in the inventory, rather than somewhere else. The rule of thumb is that, whenever something dies and then comes back to life, it should respawn right at the place of its most recent death.
In order to ensure that this is the case, we must come up with a separate heaven for each domain - one for the world, and another one for the inventory.
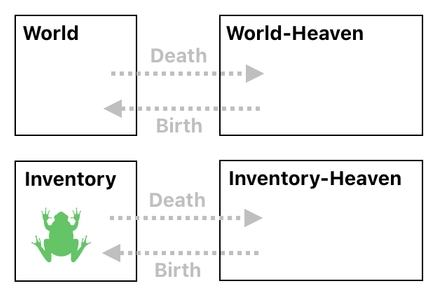
When the frog dies in the inventory, it enters the inventory-heaven (which is the place where dead inventory items hang out before they decide to reincarnate).
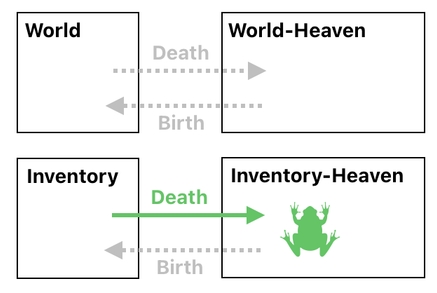
The frog stays there, up until the point at which it happens to resurrect. When such a moment comes, it exits the inventory-heaven and respawns in the inventory (i.e. the place it left when it died).
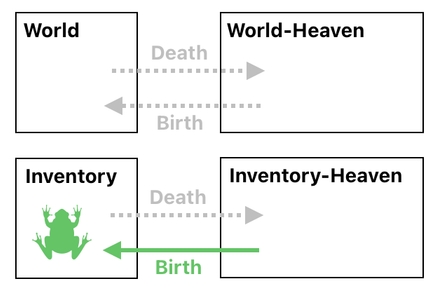
The same logic applies to the world and its corresponding world-heaven. If the frog were within the world (instead of the inventory) while it was dying, it would have entered the world-heaven rather than the inventory-heaven, and would have come back to the world again when it revived.
And, just like in the case of Earth and Heaven, we can assign distinct numerical values to the aforementioned earthly domains and their respective heavenly domains (like the ones shown below).

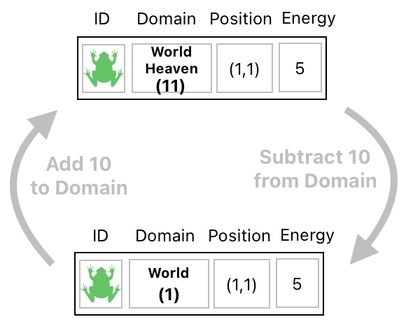
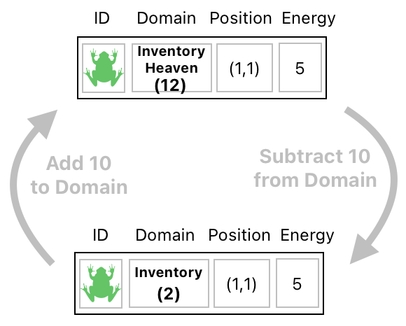
Here, you may have noticed that the world-heaven differs from the world by 10, and that the inventory-heaven differs from the inventory by 10. This means that, whenever we add 10 to a domain, we will obtain its associated heaven to which the domain's residents will go when they die.
So, for example, let's assume that our frog is currently residing in the world. We can kill it by adding 10 to its domain value, which will change its domain from the world (1) to the world-heaven (11). Afterwards, we can revive the dead frog by subtracting 10 from its domain value, which will change its domain back to the world.
In the case of the inventory, too, we can kill the frog by adding 10 to its domain value, which will change its domain from the inventory (2) to the inventory-heaven (12). And then of course, we can revive the dead frog by subtracting 10 from its domain value, which will change its domain back to the inventory.
Note here that, regardless of whether the frog is in the world or the inventory, we can always just add 10 to its domain to kill it, as well as subtract 10 from its domain to revive it. This kind of consistency allows us to deal with life and death without having to keep track of who is in the world, who is in the inventory, etc.
Previous Page Next Page
© 2019-2025 ThingsPool. All rights reserved.
Privacy Policy Terms of Service