
Author: Youngjin Kang Date: September 6, 2025
This article is Part 9 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
Let us recall the data table we have been examining so far. It is reproduced below.
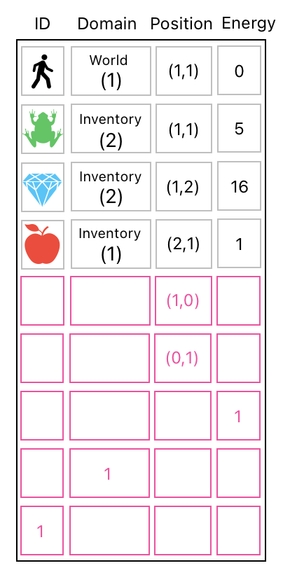
At this point, you may have realized that the content of our data table can be divided into 3 major groups - (1) rows which belong to the world, (2) rows which belong to the inventory, and (3) rows which do not belong to anywhere.
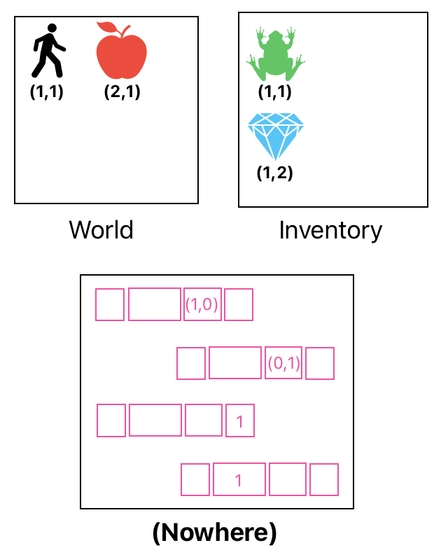
As long as a row has an ID associated with it, we can imagine it as a uniquely identifiable object in our game - whether it be the player, an item, an enemy character, a sprite, a particle effect, or whatever. It is something which possesses its own identity, which makes it distinguishable from every other row in our data table.
Rows whose ID values are empty (zero), on the other hand, are quite special in the sense that they cannot be distinguished from one another based upon their IDs. Instead, they must be distinguished based upon the roles they play in the context of creation, destruction, and transformation.
Previously, I had mentioned that these special rows are "building blocks of transformation" when it comes to shifting the numerical properies of each object by some predetermined amounts (i.e. constants).
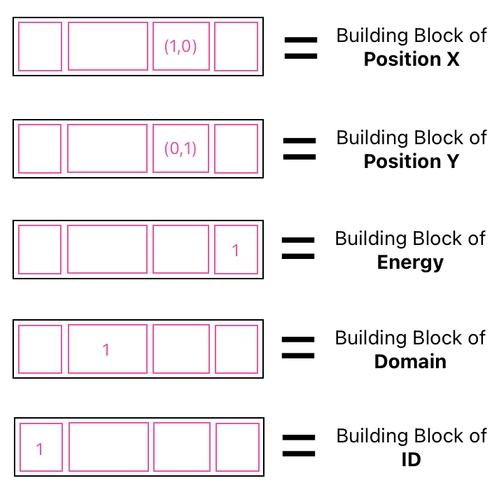
However, it is equally true that the objects themselves are made of such building blocks in the first place, just like physical entities (i.e. materials) are made of atoms. By composing these fundamental units of existence, we can give birth to any type of object.
A list of building blocks is basically a toolset which the gameplay system can leverage to create anything which is able to be generated out of their combination. Here, let me demonstrate what I mean by this. First of all, let us create a data table which is only made up of building blocks and nothing else.
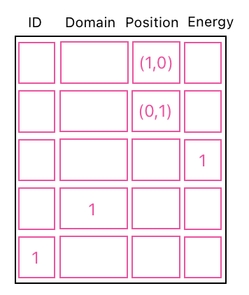
This table represents an "empty universe". It is empty because there is no object in it - no player, no item, nothing whatsoever. However, it still has the potential to bring a plethora of things into existence because it is equipped with a set of construction materials which, when combined, can manifest themselves into tangible bodies.
As we all know, an empty universe is boring. Since there is no object occupying it, its infinite horizon of vacuum is ruled by complete lethargy, never venturing to utter a spark of curiosity. In order for something interesting to happen in this universe, therefore, we must fill it with new objects.
To kickstart such a process, let me first spawn a frog in this ocean of emptiness.
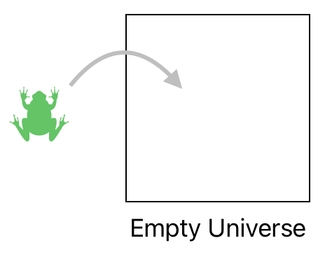
How to spawn a frog? To achieve this goal, we need to take two major steps. First, we will need to create a brand new frog. Second, we will need to put that frog into the universe.
Let me begin with the first step - creating a frog. Suppose that the new frog I am trying to make is located at the position of (1,1), belongs to the inventory, and has the energy level of 5.
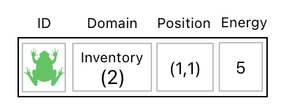
Conjuring this particular frog out of nowhere might feel like a daunting task, but it will turn out to be pretty easy if we imagine the frog as a combination of building blocks.
For instance, think of it as the result of combining 1 copy of the X-position building block, 1 copy of the Y-position building block, 5 copies of the energy building block, 2 copies of the domain building block, and 2 copies of the ID building block.
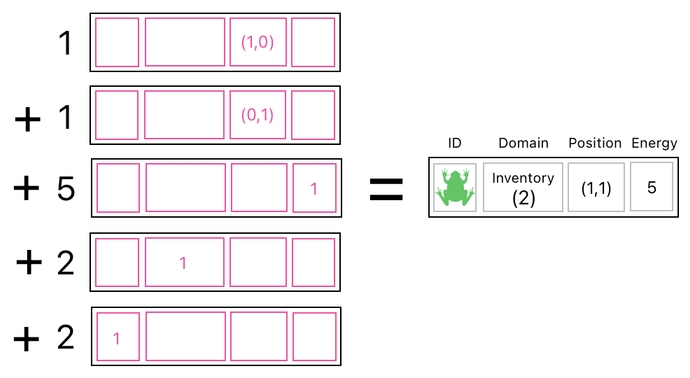
This process, in fact, can be expressed as a matrix multiplication like the one shown below. Here, we are multiplying our empty universe (i.e. list of building blocks) by a row vector whose numbers tell us how many copies of each of the building blocks we need to collect in order to assemble the aforementioned frog.
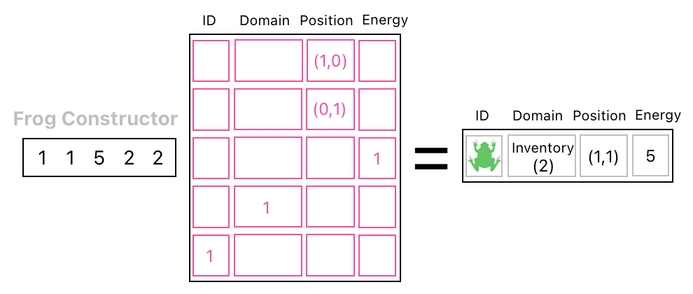
Okay, this completes our first step. We now know how to create a frog.
Let us move on to the next step. Here is the question which needs to be answered: How shall we put this frog into the universe?
Remember that our universe is currently empty; it consists only of building blocks (Nothing tangible yet whatsoever).

In order to place our new frog in it, therefore, we must add a new row to the table and fill it up with the frog's content. We can accomplish this by generating a copy of our original data table, and then making sure to attach an extra row to it which represents the frog.
The former can be achieved by selecting all of the original rows in the same order as before, and the latter can be achieved by also "selecting" a particular combination of the building blocks which results in the frog.
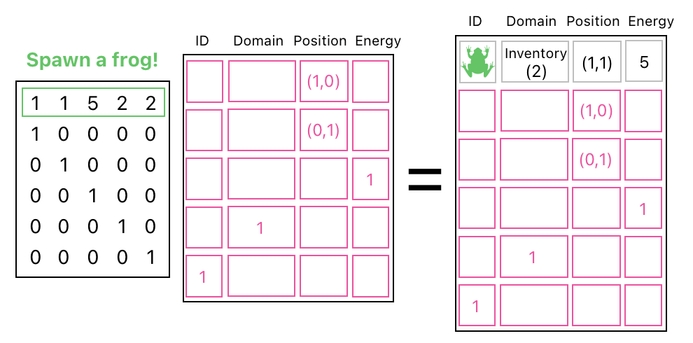
This is how we can spawn a frog inside the game.
Now that we know how to spawn a frog, it is time to ensure that we are also able to despawn it at some point in time. If we happen to keep adding more and more frogs to the world without any means of getting rid of them, it will eventually end up having no room for anything but frogs.
How to destroy a frog? Or, more generally speaking, how to destroy something which is part of the universe? Remember that each "thing" is essentially just a row in the data table. Each row represents a thing (aka "object") which is located somewhere in the game world, and its column values represent the thing's properties (such as "ID", "Domain", "Position", etc).

If we want to get rid of a single "thing" from our universe, therefore, we will have to delete the data table's row which corresponds to it.
First of all, we can clearly tell that when we select "nothing" at all (by selecting none of the rows in the table), we end of just getting an empty row, whose values are all zeroes.
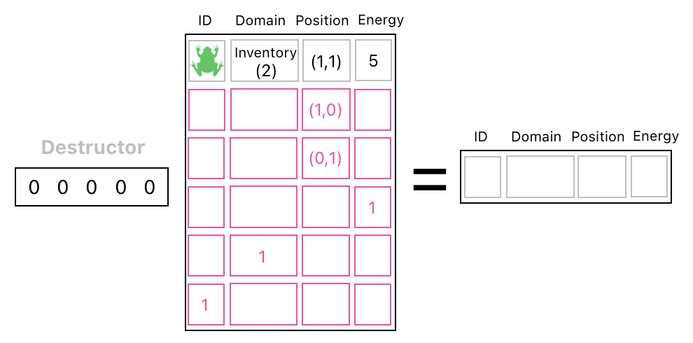
An empty row like this, such as the one illustrated above, corresponds to a chunk of empty space (i.e. vacuum).
The act of despawning our frog, then, will be equivalent to the act of simply transforming the frog's row into an empty row, while keeping the rest of the table the same as before. And the way we do this is depicted below.
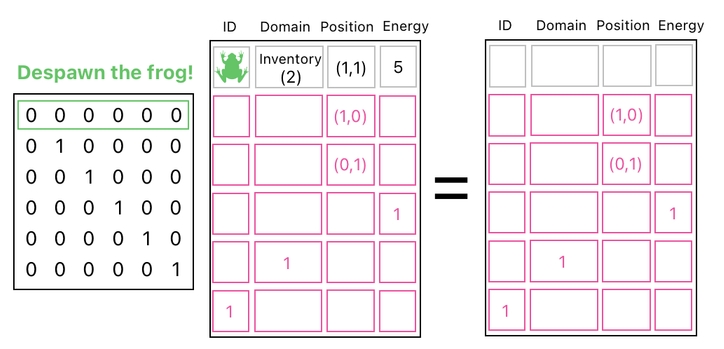
Here, you can see that we are selecting "nothing" in place of the frog's row, thereby clearing it out entirely. Meanwhile, we are also selecting all the other rows of the table in the same exact order as before, thereby preserving them without any modification.
We've seen that it is fairly easy to create and destroy things. As long as we know the right recipe for the type of object we want, we must be able to spawn it anywhere as well as despawn it at some point in time.
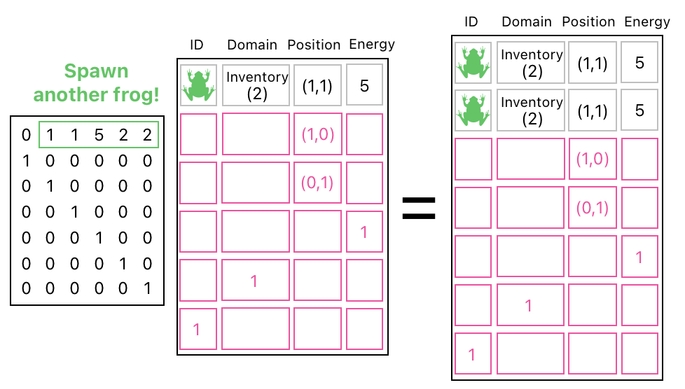
There has been a bit of inconvenience, though, in terms of the size of the data table. As you saw in the previous example, adding a frog to the world made us attach an extra row to the table, which inevitably changed its height from 5 rows to 6 rows.
And you know what? If we wish to add another frog to the world, we will then have to multiply our data table by a matrix of a different size so as to grow the table's height from 6 rows to 7 rows, like the example shown here:
And guess what? If we want to add yet another frog, we will have to come up with yet another matrix whose size is different from the previous ones, so as to grow the table's height from 7 rows to 8 rows, and so on.
This kind of inconsistency is pretty annoying, and we would like to avoid that. Fortunately, there is a simple way to prevent this. The only thing we need is to pre-allocate a bunch of empty spaces at the very beginning, so that we won't have to increase the table's size to make room for a new object.
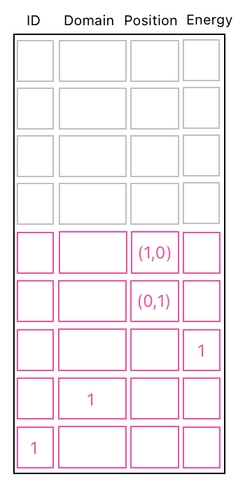
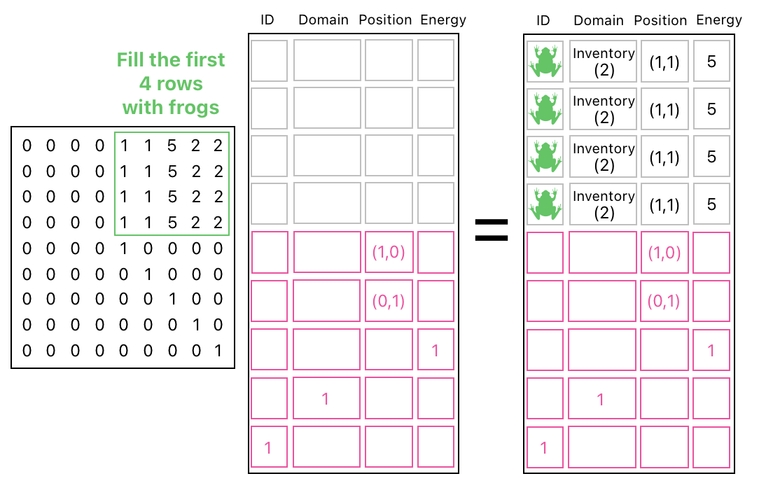
The number of such empty spaces is the same as the maximum number of objects which can simultaneously occupy the world without having to expand its volume. In the picture below, for instance, we are clearly able to spawn 4 frogs without changing the table's size at all.
 Previous Page
Next Page
Previous Page
Next Page

© 2019-2025 ThingsPool. All rights reserved.
Privacy Policy Terms of Service