
Author: Youngjin Kang Date: September 2, 2025
This article is Part 8 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
We have seen so far that there are two alternative manners in which our gameplay universe can be modeled. Firstly, I introduced a model where the game world is partitioned into distinct regions, each of which can be considered a separate physical space.

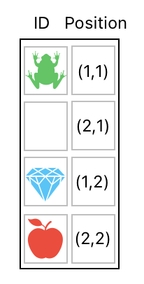
Later on, I introduced a better model where the position of each item (object) is represented not by the position of its corresponding data entry in the list, but by an explicit "position" value which is written inside the data table.
Here is something I missed, though, which I ought to go over before showcasing other concepts.
Initially, I proposed the feasibility of allowing both the physical game world and the player's inventory to coexist within the same gameplay system, by partitioning the data table into two distinct regions - one for the world, and the other one for the inventory.

This made sense because, in this early model, the table itself could be thought of as a direct physical analogue of the actual gameplay space. Splitting the table into two groups of rows, therefore, was practically the same thing as splitting the game's physical space into two areas.
But then, as I introduced the concept of representing positions as numerical properties (i.e. explicitly written values), such a one-to-one correspondence between the data table and the physical space suddenly disappeared. Since each row is no longer bound to a fixed point in space, we can no longer generate two spatial volumes by partitioning the table into two groups of rows.

And the problem is that, for rich gameplay experience, we need separate spaces in our game which are designed to serve different purposes. We want the inventory besides the world, so as to let the player open up his inventory as a simple UI menu at any point in time by just clicking a button on the screen. Otherwise, the player will have to physically carry every one of his items whenever he moves from place to place.
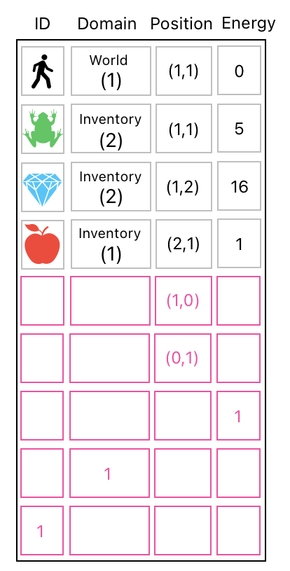
Let us revisit our previous example, in which our data table consisted of 7 rows - 4 for the inventory items, and 3 for the basis of position/energy modification.
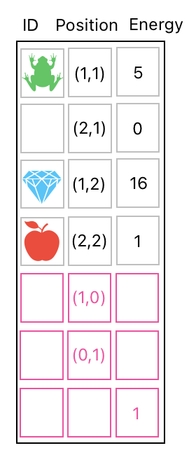
Now imagine that, in addition to inventory items, we also want to have the actual gameplay space (i.e. some 3D environment, filled with physical objects), in which we can see and control the player character.
How to establish this kind of division? For this purpose, we first have to explicitly label our data table's rows with the domains to which they belong. We can achieve this goal by introducing a new column called "Domain".

As you can see, our 3 inventory items (i.e. frog, diamond, and apple) now have "inventory" as their domain values. This means that these 3 items are all located within the inventory.
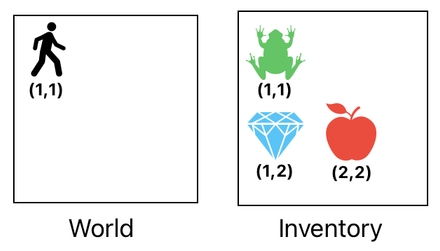
Now, let us add an additional row to represent our player who resides not in the inventory, but in the game world (i.e. the actual physical space where gameplay happens). In order to denote such a relation, we can set the term "world" as the player's domain.

Here we have two different domains - the world and the inventory. The world is the physical space in which the player lives. The inventory, on the other hand, is a completely isolated space which is filled with the player's items.
These two domains possess their own coordinate systems. The pair (1,1), for instance, may either indicate the position of the player or the frog, depending on whether the domain is set to "world" or "inventory".
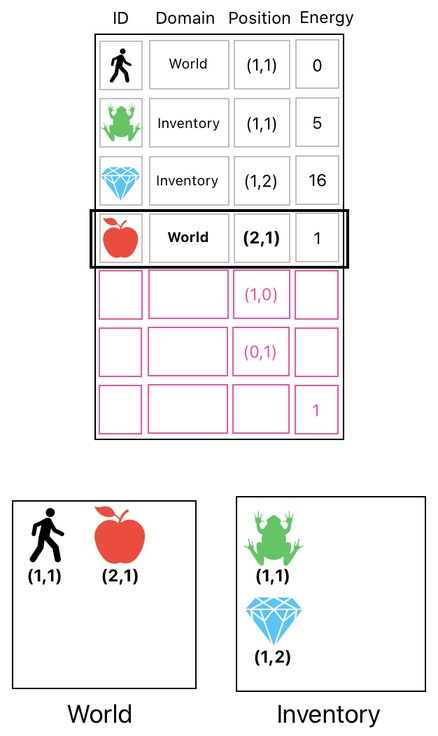
Although domains are isolated chunks of space, it is possible to "teleport" an object from one domain to another by simply converting its domain value. If you want to pull the apple out of the inventory and place it right in front of the player, for example, you can accomplish this task by modifying not just the apple's position, but also its domain (from "inventory" to "world").
Changing the domain, though, may seem impossible at first because it is not a number (which means we cannot add or subtract it inside a matrix multiplication). As we put a little bit of thought to it, however, we begin to realize that we can bypass such an obstacle by assigning a numerical value to each domain value. For instance, nothing prohibits us from supposing that number 1 indicates "world" and number 2 indicates "inventory" (0 indicates "no domain").
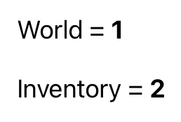
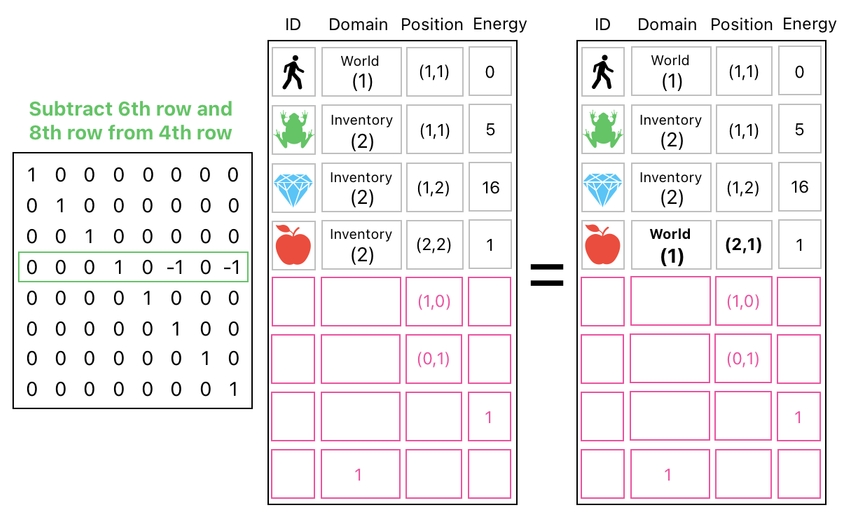
Based upon this these rules, we can then proceed to either increase or decrease an item's domain value by adding/subtracting a number. Here is how we can do it. First of all, let us make yet another row in our data table, whose values are all zero except the domain part which is set to 1.

This new row lets us change the domain of any item. Since the current domain of the apple is 2 (inventory) and the goal is to turn it into 1 (world), all we have to do is subtract it by 1, which is equivalent to the subtraction of the apple's row (i.e. 4th row) by our new row (i.e. 8th row).
Besides doing this, of course, we will also need to change the Y-coordinate of the apple's position in order to place it in front of the player. The full process is illustrated below.
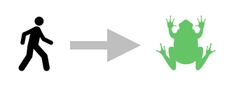
In the same spirit, we also have the ability to transform one type of object to another simply by offsetting its ID value.
Here is an example. Imagine that a sorcerer cast a magic spell to the player, turning him into a frog.
How shall we make this transformation happen in our game? The solution is pretty similar to the one we saw in the previous case. Just like what we did with the domain, the first thing we ought to do is assign a number to each ID value.
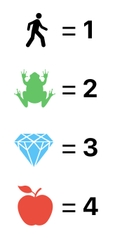
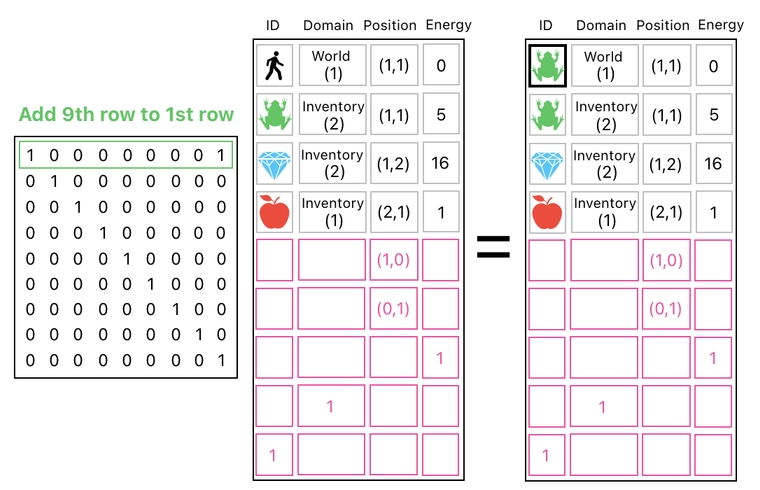
Now that we are representing our IDs with numbers, we are now able to convert one ID into another simply by shifting its numerical value. Since the player's ID is 1 and the frog's ID is 2 in our example, we can turn the player into a frog by adding 1 to his ID.

In order to perform this addition in the context of linear algebra, though, we will first need to append yet another row to our data table. This brand new row, which has 1 (unit value) in its ID column and 0 (no value) in every other column, will let us shift the ID value of any object by any amount we want.
By adding this row to the player's row, we can effectively add 1 to the player's ID, thereby changing the identity of the player to that of the frog.
But, if you are annoyed by sorcerers who are habitually turning people into frogs without facing legal repercussions, you may want to ban them from exercising such a sort of magic altogether. And you know what? You can enforce such a rule by erasing the "1" from the last row we just added, which can be done by zeroing out the entire row.
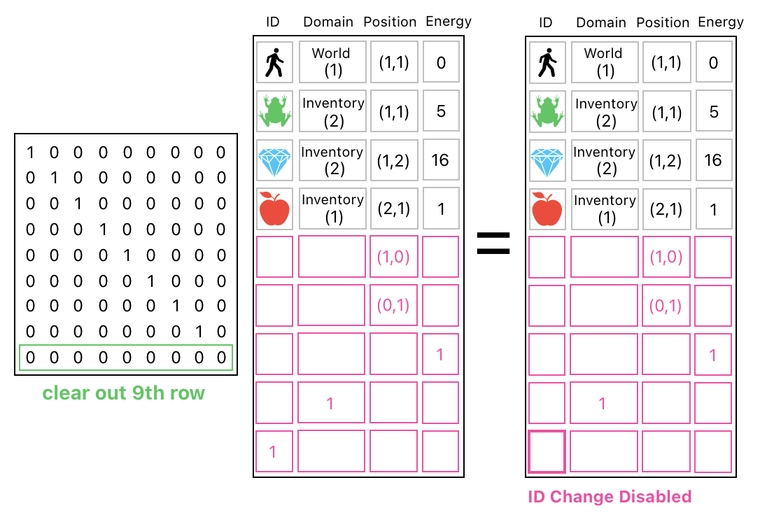
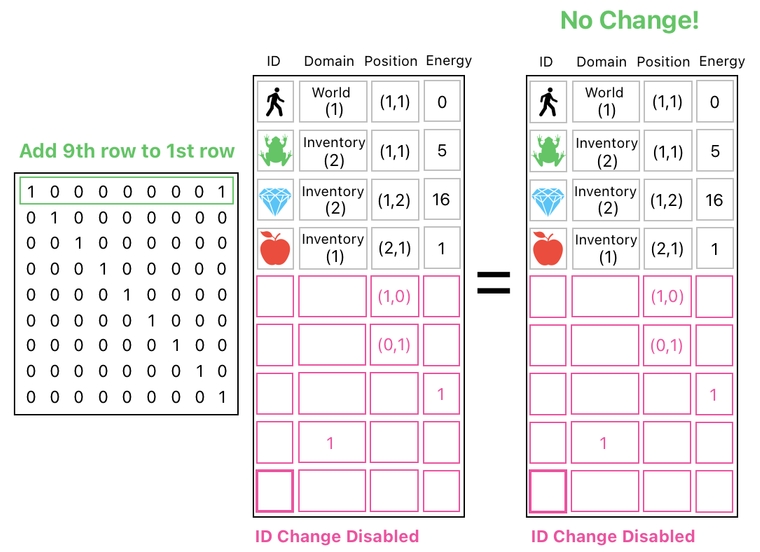
This will block anyone from modifying the ID value anywhere inside the game. Henceforth, if you attempt to turn the player into a frog by adding 1 to his ID value, you will be able to confirm that the player's ID won't change because adding an all-zero row has no effect (See the picture below).
 Previous Page
Next Page
Previous Page
Next Page

© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service