
Author: Youngjin Kang Date: August 29, 2025
This article is Part 7 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
In the previous article, I explained how each item's position in the inventory can be represented not by its location in the data table (i.e. row and column), but by a numerical property associated with it. And for such a purpose, I introduced an additional column in the data table called "position", which is filled with the items' positions.
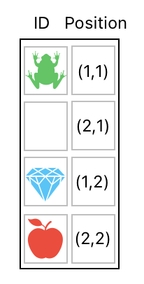
The biggest advantage of handling positions this way is that, since all the position values are aligned in a single column, we can manipulate the items' locations simply by modifying this particular column alone, without modifying any of the other columns.
In addition, there are other major benefits offered by this solution. First of all, since the data elements in the "position" column are just numerical values (i.e. XY coordinates), the range of positions that each item can have is unbounded. That is, nothing stops us from imagining our inventory of items as an infinitely wide 2D plane, since any combinatiion of X and Y values can be used to represent an item's position in the inventory.
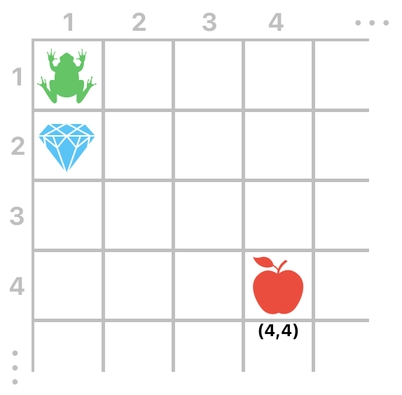
Another benefit is that, since the location of each item is no longer exclusively bound to an entry in the data table, we are now able to overlap an item on top of another by setting their positions to the same value.
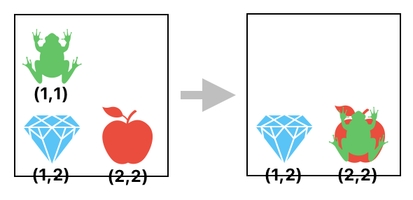
And the way we do this is simple. We first separate out the column of position values (just like we've done before), and set the position of one of the items to be identical to that of the other item.
Furthermore, since there is no rule which says that the XY coordinates must be integers, we are free to locate our items at any non-discrete points in 2D space. For example, it is completely fine to put our frog somewhere in between a pair of adjacent grid cells.
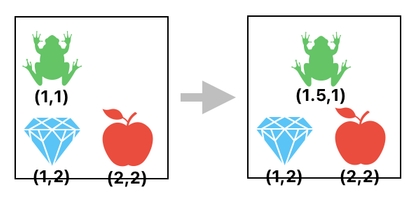
Making this kind of movement, however, is a bit tricky. In the example shown here, we cannot simply swap the position of the frog with that of the empty grid cell, since it will put the frog right at the center of that cell.
Suppose we are trying to push the frog to the right by just a half of a grid cell (i.e. 0.5). In this scenario, what we really want is to add the value of 0.5 to the frog's X-coordinate, which is equivalent to the addition of (0.5,0) to the position value.
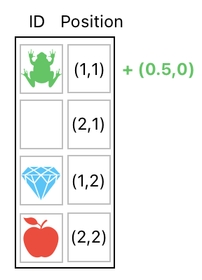
How to let this happen, in the context of linear algebra? For sure, you might have already guessed a quick solution which technically works. After splitting up the data table's columns, we can just add a column of "offset values" to the column of positions to be able to see the desired consequence.
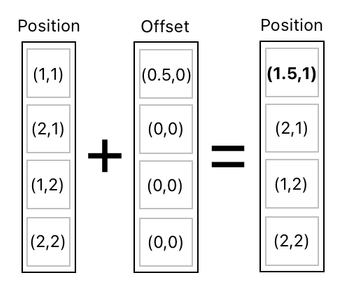
This works. However, it is a bit too cumbersome from a computational perspective. I would insist that there must be a better way, and indeed there is! Here, I will present you with an alternative method which is far more elegant.
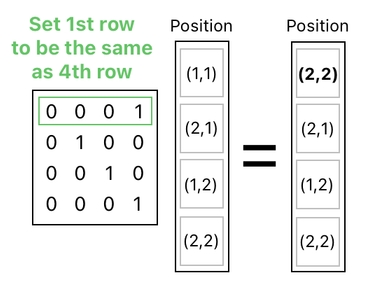
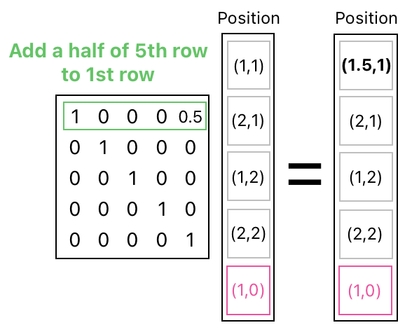
The first thing we will need is to add an extra row to our data table, whose "position" value is set to (1,0). All the other column values in this row are set to zero (empty).
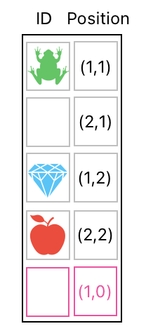
We can then add 0.5 to the X-coordinate of our frog's position by means of not a brute-force addition of two columns, but a matrix multiplication. You can see how it works in the picture shown below. The matrix on the left side takes a half (0.5) of the last element of the column values (which is (1,0)) and adds it to the first element (which is the frog's current position).
What's good about this approach is that it lets us do many things at once, within the context of a single matrix multiplication. In order to illustrate what I mean by this, let me show you a slightly more advanced example.
Let us imagine that, in addition to moving the frog to the right by 0.5, we also want to move it downward by 0.5. This corresponds to the act of adding (0.5, 0.5) to the frog's current position, which yields the new position: (1.5, 1.5).
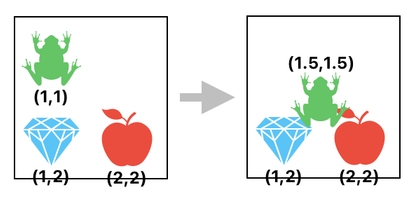
How to add the value of 0.5 not just to the frog's X-coordinate, but also to its Y-coordinate?
If we look back at the previous data table, we can clearly see that the extra row we added has (1,0) in it as its "position" value. We have seen that, by scaling this row by 0.5 (which turns (1,0) into (0.5,0)) and adding it to the frog's row, we are able to add 0.5 to the frog's X-coordinate.

Since the Y-coordinate of this special row is 0, however, we are unable to make it change the frog's Y-coordinate no matter how much we scale it.
In order to move the frog vertically, therefore, we need another special row designed to shift its Y-coordinate. Let us add a new row, this time with the "position" value of (0,1) instead of (1,0).
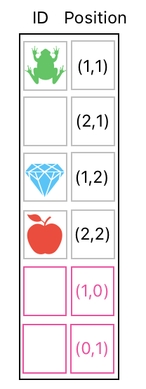
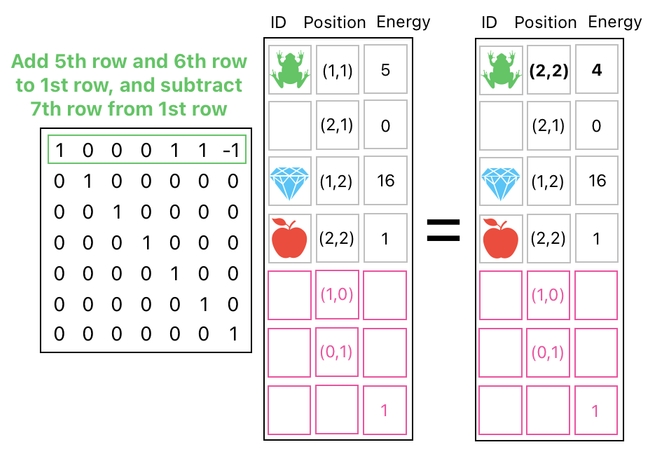
Then, guess what. Now we are able to shift our frog's position both horizontally and vertically, by adding scaled versions of both the 5th row and the 6th row. The 5th row has (1,0) in it, so scaling it by 0.5 and adding it to the frog's row will shift the frog's position by (0.5,0). Meanwhile, the 6th row has (0,1) in it, so calling it by 0.5 and adding it to the frog's row will shift the frog's position by (0,0.5). Together, they end up shifting the frog's position by (0.5,0.5).
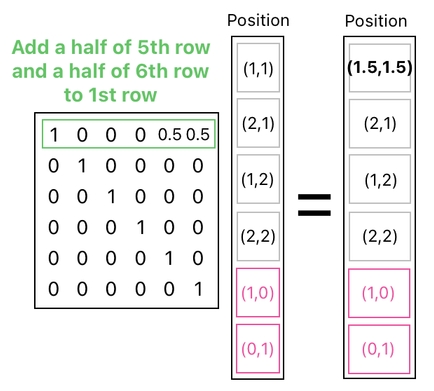
Aside from technical details, the overarching idea is that the extra rows we just added (i.e. (1,0) and (0,1)) are the fundamental building blocks (aka "basis") out of which any motion can be composed. Think of these rows as a pair of buttons you can press to move the frog.
So, what makes this solution particularly attractive, as opposed to just writing up a column of position values and adding it to the existing one (like the one shown below)?

The answer is that it lets us pack a variety of events in a single matrix multiplication. Suppose, for example, that our items possess not only positions, but also energy numbers as their properties.
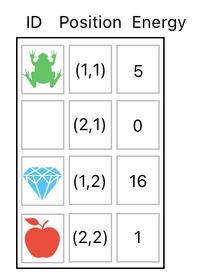
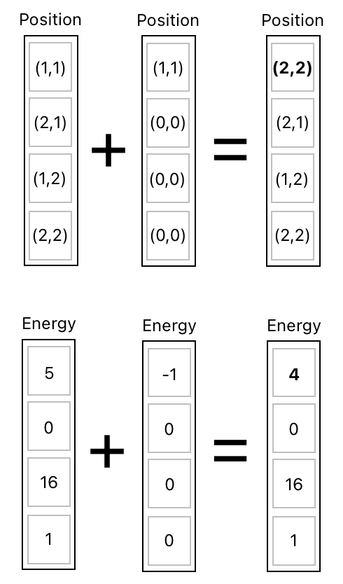
Now imagine that our frog, initially located at (1,1), decided jump on top of the apple (which is located at (2,2)). By the act of jumping, the frog consumed a bit of its energy, thereby decrementing it from 5 to 4.
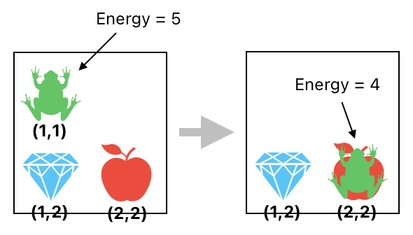
If we model this set of events as a set of transformations in our data table, they will looks like the ones shown below. Here, you will see that the frog's position changed from (1,1) to (2,2), while the frog's energy changed from 5 to 4.
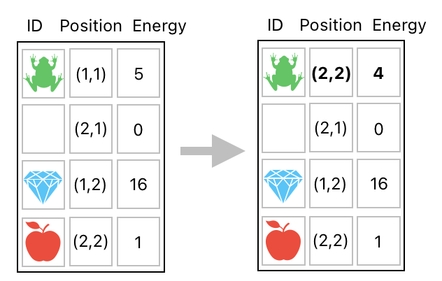
The question is, how to execute these two separate changes? Technically speaking, we can definitely choose to first split up the table into individual columns,
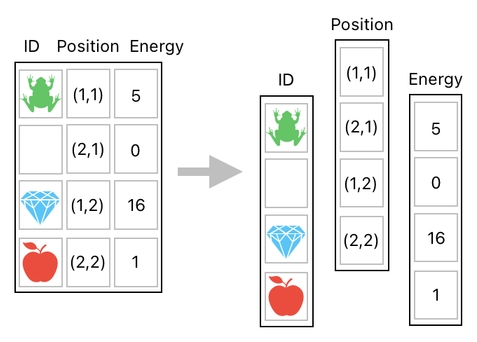
Individually update the position-column and energy-column by adding two different column values to them,
And then recombine the resulting columns to obtain the modified data table. Pretty straightforward! However, this approach is too cumbersome in the sense that it requires us to separate out the columns and go over a multitude of additions just to simulate the effect of a frog losing a bit of its energy while jumping.
A much more scalable method is to carry out all the required transformations inside a single matrix multiplication. In order to do that, we will first need yet another extra row in our data table (besides the ones for X,Y movements) which serves as a building block for modifying an item's energy value. It is a row which has the value of 1 in its energy-column and 0 everywhere else.
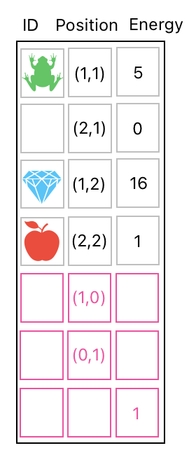
With this new tool, we can then update both our frog's X,Y coordinates AND its energy value simultaneously (See the picture below).
 Previous Page
Next Page
Previous Page
Next Page

© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service