
Author: Youngjin Kang Date: August 25, 2025
This article is Part 6 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
It has clearly been proven that, by applying two different matrix multiplications to our data table (one on the left, and the other one on the right), we are able to manipulate both rows and columns.
One of the most basic things we can do in our game world is to move items from place to place. And the two-dimensional nature of matrices suggests us that it is possible to make 2D movements by playing with rows and columns.
To demonstrate this point, I will come up with a slightly modified version of the player's inventory. What you are seeing below is an inventory of items which is not a list, but a 2x2 grid of items.

Here is a quiz. What will you do if you are asked to move the frog to the right?
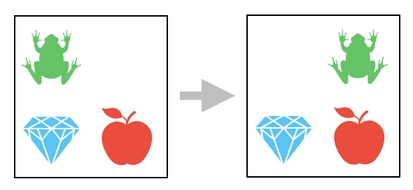
As you can probably tell, simply swapping the two columns of the inventory is not going to work. It is because we do not want to modify the bottom row; all we need is flip the two items on the top row - not the ones on the bottom.
In order to solve this problem, then, we must handle the two rows separately. And for this purpose, we need to first split the rows and convert them into two separate tables. This can be done by making two row selections in parallel - one which selects the first row, and the other one which selects the second row.
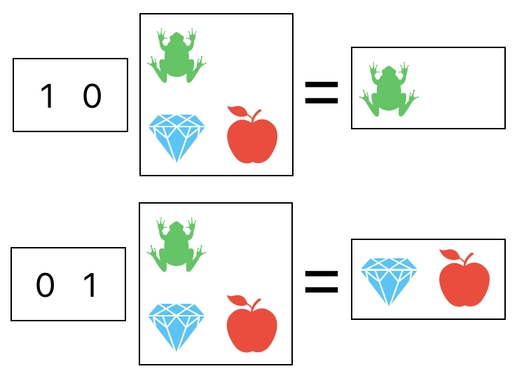
We don't need to do anything with the second row because the diamond and apple are supposed to stay where they are. The only row we need to modify is the first row, where the frog is located. In this row, all we have to do is just swap the two columns, which will effectively swap the frog with the empty slot on its right hand side.
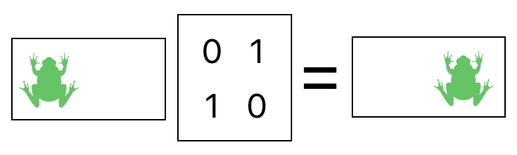
This basically moves the frog to the right. The only remaining step is to recombine the two rows back to the single 2x2 grid format, so as to recover the original dimensions of the inventory. To do that, we first need to attach an extra row to each of these two isolated rows for the purpose of synchronizing their sizes with that of the final result (i.e. 2x2).
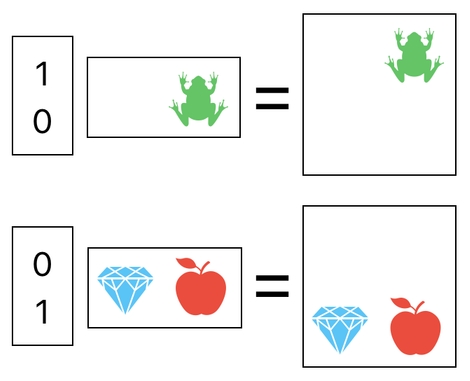
Then, we just need to add these two 2x2 results together to obtain the final result, which is exactly what we would expect after moving the frog from the left to the right.

Here is another quiz. What will you do if you are asked to exchange the positions of the frog and the apple?
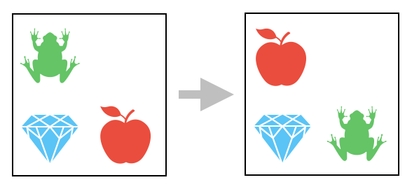
This one is trickier to solve. Since it involves diagonal movements (e.g. the frog needs to move not just rightward but also downward), we cannot simply split this 2x2 inventory either by two rows or by two columns. The former will let us move the frog to the right, but not to the bottom. The latter will let us move the apple to the top, but not to the left.
So, how shall we resolve this set of conflicting goals? While there might be more efficient ways, one method which is easy to understand is to break this problem down to a series of smaller problems.
When we think of a swap between the frog and the apple as a sequence of simple movements (each of which is either horizontal or vertical but not both), it leads us to imagine that such a diagonal swap can be achieved by first swapping the frog with the empty slot on its right, swapping the frog with the apple, and then finally swapping the apple with the empty slot on its left.
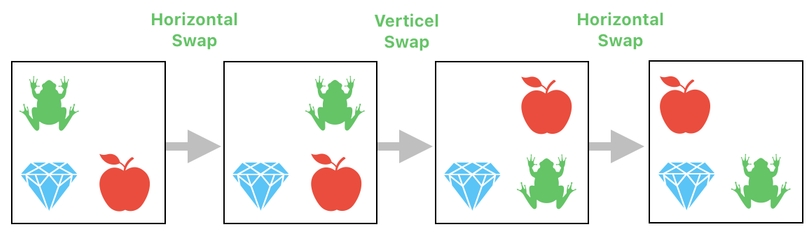
Each of these 3 simple movements, then, can be further broken down into a list of matrix operations. For a horizontal swap, we first split the inventory into two rows, reverse one of them, and then recombine them. For a vertical swap, we first split the inventory into two columns, reverse one of them, and then recombine them.
At this point, however, you may be thinking that I am overcomplicating things. And yes, it indeed is the case. The number of calculations needed for carrying out even a single diagonal swap between a pair of items is way too large, and it makes us seriously question the sanity of how we have hitherto been representing positions/movements.
The root of the problem is that we have been equating the coordinates of matrix entries with those of physical positions in the inventory. We have been accustomed to say that the apple is on the right side of the diamond, for example, if the apple's entry is located on the right side of the diamond's entry in the matrix.
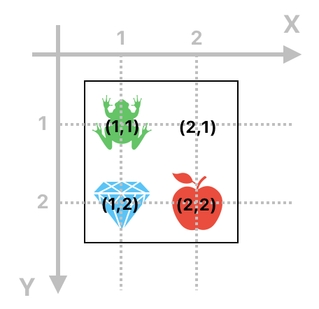
While is kind of representation feels highly intuitive and easy to understand, it challenges us with loads of technical difficulties when it comes to making any modifications to it. Since it forces us to model every change in location as an exchange of rows/columns in the matrix, we have no choice but push ourselves through a bunch of cumbersome processes just to accomplish things that are so trivial.
At this point, therefore, we need to think of a better solution. Here is my thought.
What if we just start treating each item's position as a numerical property, written as one of the elements in the matrix (i.e. data table)?
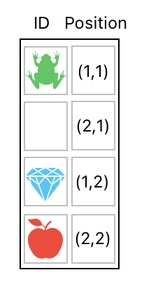
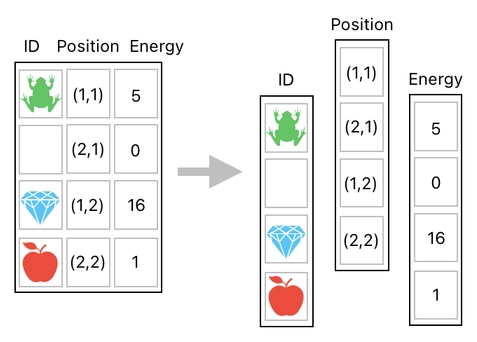
Here, I am explicitly stating the positions of the items (i.e. XY coordinates) inside a whole separate column, while listing each of the items as a row in the data table. This way, we no longer have to match the size of our data table with that of the actual inventory. In this example, the inventory itself is still 2x2 in size (as you can tell from the fact that both the X and Y coordinates range from 1 to 2), but our data table doesn't have to be of that size.
What makes this approach so elegant is that it lets us no longer treat positions in a special manner.
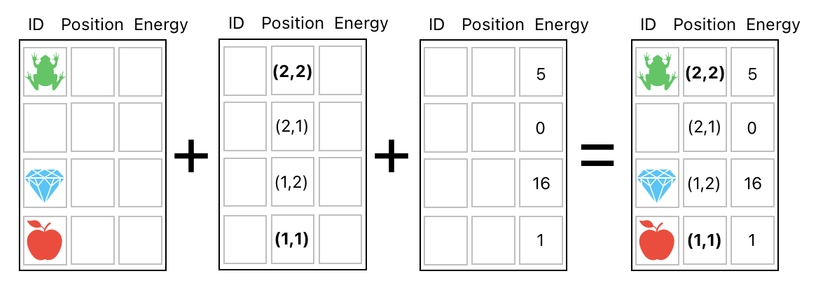
Take a look at the table below; it has an extra column called "energy", meaning that we are now allowing each item in the inventory to have its own energy level associated with it.
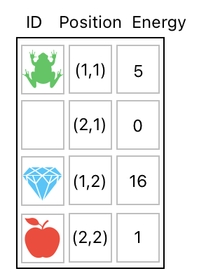
As you can clearly see, there is no difference from "position" and "energy" from a technical point of view. They are both columns in the data table, filled with numerical values. If we want to change the positions of the items, we no longer have to modify the structure of the table itself; we just need to fiddle with their "position" property values, which are all listed in the second column.
And since they are all part of the same column, modifying their values is straightforward even in cases of diagonal movements.
Let us go back to the previous problem of swapping the frog and the apple.

This problem was hard to solve because we were trying to directly modify the items' 2x2 arrangement, which inevitably involved changes both in the table's rows and columns.
In our new, alternative representation of the inventory (shown below), on the other hand, the problem turns out to be far simpler.

Since all the position values are listed in the second column of the table here, we know that we only need to make changes to this particular column only. This means that we can safely discard all the other columns by splitting them apart.
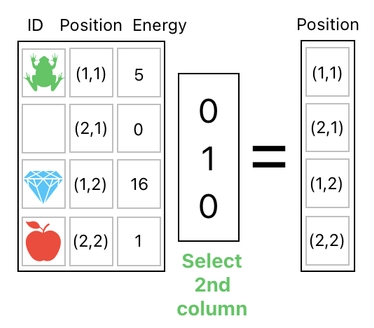
As you have seen before, the way we extract (split) each column from the data table is by selecting each of them individually using matrix multiplication.
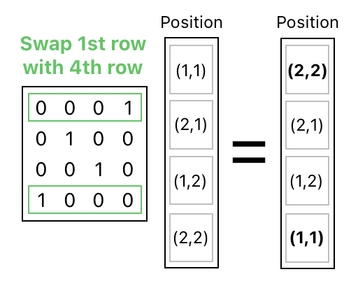
Once the 3 columns are splitted apart, we only need to modify the content of the second column (i.e. the column representing position values). Since we are swapping the frog's position with the apple's position, all we have to do is swap the column's 1st row with the 4th row.
We can then proceed to augment the sizes of the 3 separated columns to match them up with that of the original data table (i.e. 4x3). For example, the image below shows how we can append two empty columns to our second column in order to recover its place in the data table.
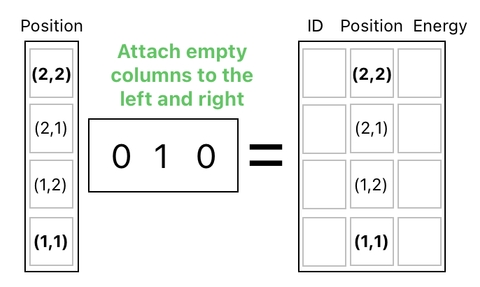
Then, we can simply add up the results of such augmentations to acquire the final state, in which the positions of the frog and apple are swapped.
 Previous Page
Next Page
Previous Page
Next Page

© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service