
Author: Youngjin Kang Date: August 21, 2025
This article is Part 5 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.
We have seen so far that it is possible to select individual rows in our data table, swap them with each other, add one of the rows to another, and so on. But what if we want to be able to manipulate not just rows, but also columns in a like manner?
In the previous article, I have shown that it is necessary for us to split the table by its columns and then recombine them later on, so as to be able to modify each of the properties (i.e. column values) without unintentionally tampering with the others.
Let me revisit the example we have been looking at. In order to handle the two properties (i.e. ID and energy) separately, we must first separate out the table's two columns.

Then, after modifying them individually (by means of matrix multiplication), we must be able to rejoin these two columns back to the original form.

Let's see how we can manage the splitting part. First of all, I would like to tell you that the act of splitting is basically the same thing as executing the following two tasks:
(1) Select the first column of the table.
(2) Select the second column of the table.
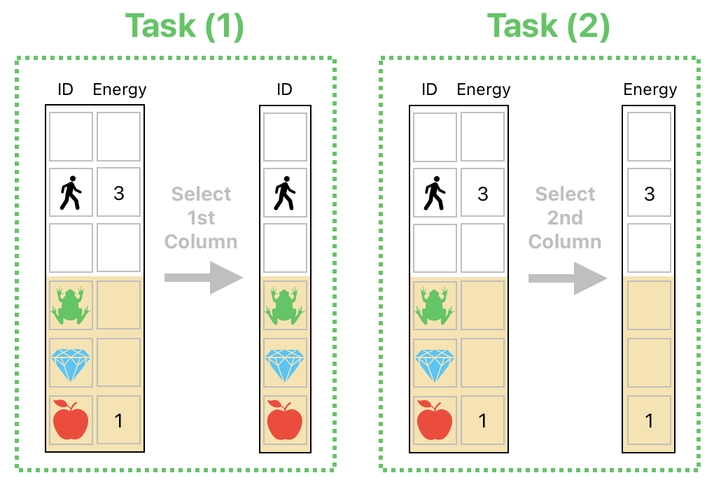
One noteworthy point is that these two must be carried out separately. Let me begin with the first one - the process of selecting the first column.
How shall we manage to select only the first column of the table, leaving out the second column? The answer is that we can't, as long as we choose to multiply a matrix on the left side of the data table.
If we choose to multiply a matrix on the right side of the data table, however, it will let us select the individual columns of the table instead of rows. Here is how it works.
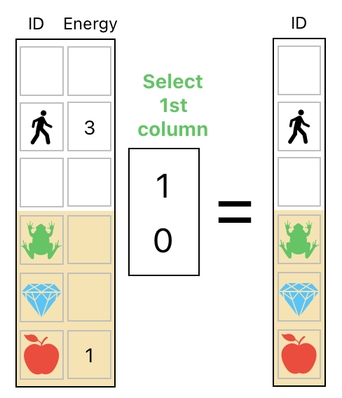
What you are seeing here is an act of selecting a column. This example selects the first column of the table in particular, since we are multiplying it by a selector (i.e. a column vector) whose first entry is 1. If you carry out the multiplication, you will realize that it does indeed result in the first column of the original table and ignores the second column.
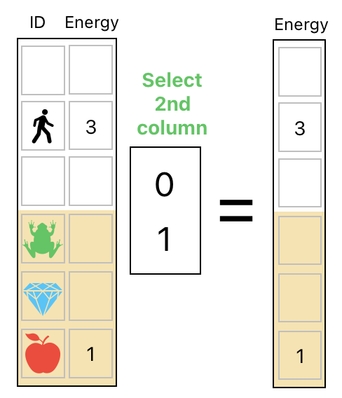
In contrast, we can select the second column of the table by setting the second entry of the selector to 1.
As a side note, I would also like to mention that it is also possible to select multiple columns at once by putting multiple selectors in one place.
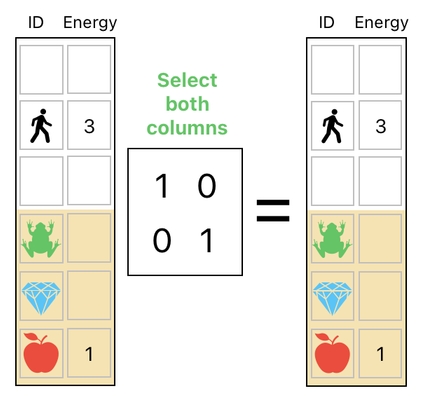
This leads us to the realization that there are two different ways of selecting a portion of our table - selection by rows and selection by columns.
The core idea is that, by multiplying the table by some kind of "selector", you can select either a row or column of that table. If this selector is a row of numbers which is placed on the left side of the table, it will return a row.
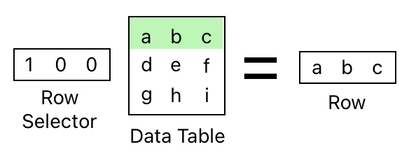
If you put a multitude of such selectors in parallel, you will be able to select multiple rows at once.
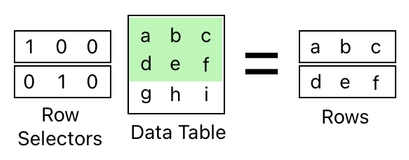
On the other hand, if the selector happens to be a column of numbers which is placed on the right side of the table, it will return one of the columns of the table instead of a row.
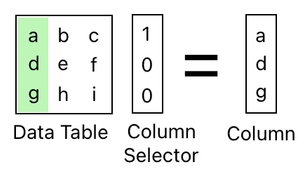
And, just like you can select multiple rows by putting multiple row selectors in one place, you can select multiple columns by putting multiple column selectors in one place.
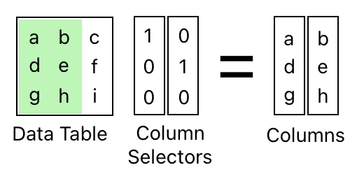
What if you decide to select both a row AND a column at the same time? The way you do this is straightforward; you just put your row selector on the left side of the table, and your column selector on the right side of the table.
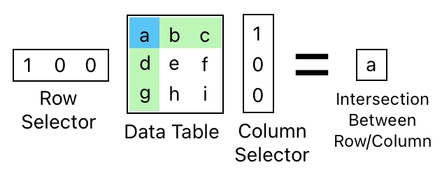
Once you do the calculation, you will soon discover that the result of this two-step multiplication is the intersection between the selected row and the selected column.
In general, though, the range of things we can do by means of matrix multiplication is a lot broader than what I just demonstrated here. Besides selection, as you already know, we are also able to swap the rows (columns), add them up, etc.
Rather than just row selectors, for instance, we may as well construct a generic "row-manipulating matrix" which, when placed on the left side of our data table, will fiddle with its rows.
Likewise, rather than just column selectors, we may as well come up with a generic "column-manipulating matrix" which, when placed on the right side of our data table, will fiddle with its columns.
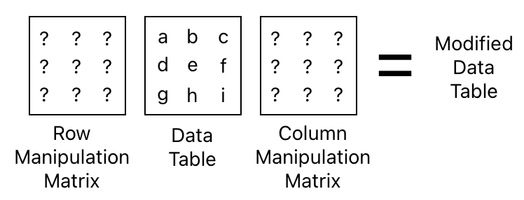
Based upon these two major building blocks, we are now able to define all sorts of sophisticated game mechanics using matrix multiplication. Since we have the power to manipulate not just rows but also columns of our data table, separately managing each individual property (e.g. ID, energy, etc) will be a piece of cake.
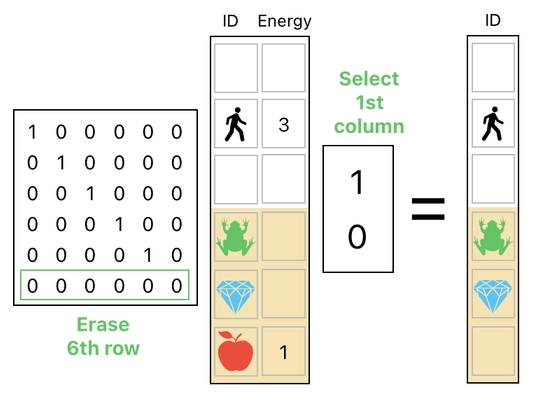
The picture below demonstrates how we can destroy the apple by simply erasing it from the player's inventory AND discarding the energy-column of the table at the same time. All we have to do is carry out the former process on the left side of the table (because it deals with rows), while also making sure to carry out the latter process on the right side of the table (because it deals with columns).
Meanwhile, we can handle the concept of energy exchange by transferring the apple's energy to the player AND discarding the ID-column of the table at the same time.
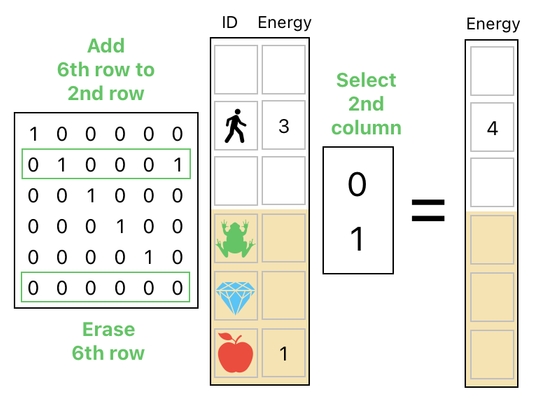
These two actions will give us the two halves of our desired result. In the first half of the result (i.e. first column), we see that the apple has been successfully removed from the inventory. In the second half of the result (i.e. second column), we see that the apple's energy has been successfully transferred to the player. The only remaining task is to join them back.

How to do this? In order to accomplish the goal of converting two single-column tables into one double-column table, we must first realize that we are trying to apply some kind of "size change" to the tables we are dealing with. Do you remember that it is possible to add extra rows (i.e. items) to the inventory by making more row-selections than the ones which are currently available?

In a similar manner, we are also able to add extra columns to our data table by making more column-selections than the ones which are currently available. For example, if we choose to make an extra "empty selection" on the right side of the ID-column, a new empty column will appear on its right side.
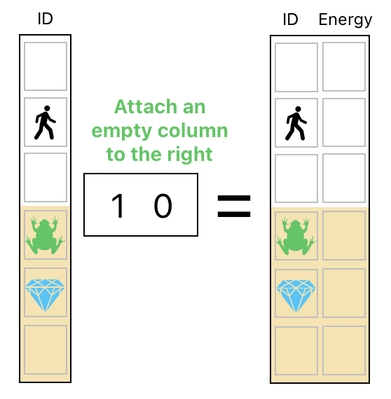
Likewise, if we choose to make an extra "empty selection" on the left side of the energy-column, a new empty column will appear on its left side.
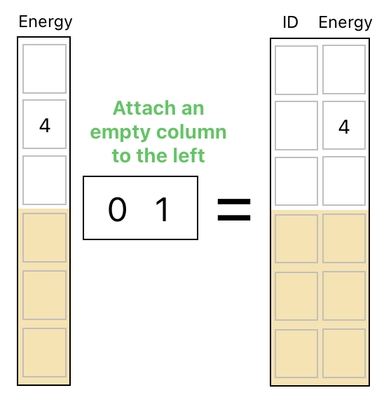
We are one more step closer to the final result. Now that the sizes of these two tables are both identical to that of the original data table (which consists of 6 rows and 2 columns), all we need to do, then, is simply add them up to finish our mission.
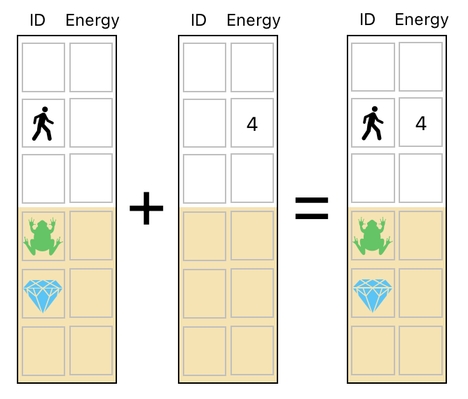
The result is exactly what we expected. The apple is now gone, and the player has successfully absorbed the apple's energy.
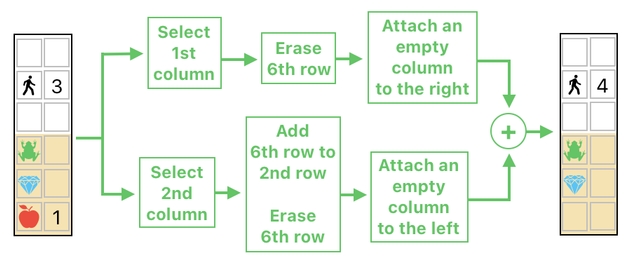
The diagram shown below depicts the full process of making the player eat the apple and acquire energy from it. As you can see, it first splits the data table into two columns, manipulates them separately, and then recombines them to recover the table's original format.
 Previous Page
Next Page
Previous Page
Next Page

© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service