이공계 출신의 게임 개발자들은 보통 수학적 모델을 사용하여 게임을 디자인 하곤 한다. 이는 스토리와 나레이션을 중심으로 하는 문학/역사 기반의 게임 디자인과는 사뭇 다른 방식이라고 할 수 있다.
그렇다면 게임 디자인에 사용되는 수학적 모델에는 대표적으로 어떤 것들이 있을까?
심시티와 심즈의 창시자인 윌라이트는 예전에 게임 디자인에 관련하여 강의를 한 적이 있었다 (나는 유튜브에 올라온 영상으로 그의 강의를 시청했다). 그 자리에서 그는 "게임은 하나의 거대한 수학적 모델 과도 같으며, 이 모델은 게임 속의 전략적 다양성이나 밸런스 같은 핵심 요소들을 조율하는 데에 있어 중요한 역할을 한다" 라고 주장했다.
이러한 의견과 더불어 윌라이트는 게임의 매커니즘으로 이용될 수 있는 몇가지 수학적 모델들을 소개했는데, 이들은 다음과 같다.
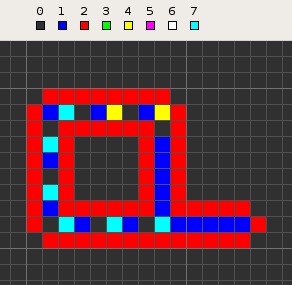
(이미지 출처: Wikipedia: https://en.wikipedia.org/wiki/Langton%27s_loops)
(1) 셀룰러 오토마타(Cellular Automata)
셀룰러 오토마타는 국내에서 종종 '셀 오토매텀'이라는 명칭으로 불리우기도 한다. 한마디로 표현하자면, 수많은 유한상태기계(유한상태머신)들이 가로/세로 방향으로 그물망처럼 연결되어 있는 모델이다. 이 모델은 수학자 콘웨이(Conway)가 라이프게임(Game of Life)을 시작으로 유행시키다가, 학자 울프램(Wolfram)이 1차원 셀룰러 오토마타의 종류를 체계적으로 정리해 발표하기 시작하면서 하나의 대중적인 수학이론으로 자리잡았다. 행과 열로 이루어진 셀(Cell) 단위의 객체들을 주기적으로 업데이트 해주는 방식으로 작동하는데, 이는 2차원 배열의 형태로써 컴퓨터 상에 구현되기 쉽기 때문에 수많은 게임 개발자들 에게 각광받고 있다.
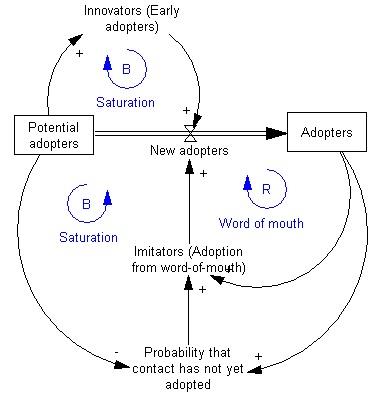
(이미지 출처: Wikipedia: https://en.wikipedia.org/wiki/System_dynamics)
(2) 시스템 역학(System Dynamics)
'시스템 다이나믹스'라고도 불리우는 이 모델은 스톡과 플로우(Stock and Flow)를 비롯한 독립적인 하위 시스템들 사이의 역동적인 상호작용을 중심으로 세워진 일종의 시스템 이론이다. 학자인 제이 포레스터(Jay Forrester)가 창시했으며, 그가 쓴 시스템 다이나믹스 관련 저서들 중 하나는 윌라이트에게 심시티의 개발과 관련하여 많은 영감을 준 것으로 알려져 있다.
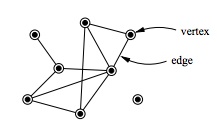
(이미지 출처: Wikipedia: https://en.wikipedia.org/wiki/Network_theory)
(3) 네트워크 이론(Network Theory)
말 그대로 수많은 객체들 사이의 얽히고 설킨 관계를 바탕으로 한 모델인데, 이것은 비록 통신공학에 가장 많이 사용되기는 하지만 종종 게임 디자인에도 사용될 때가 있다. 온라인 게임 속 클라이언트들 사이의 상호관계, 또는 심즈에 등장하는 캐릭터들인 '심'들 사이의 상호관계 모두 네트워크 이론의 범주에 들어간다고 할 수 있다. 네트워크 이론은 게임 속에서 주로 사회적 현상을 나타낼 때 사용된다고 보면 된다.