Back

Home/Library/Concepts of a Plan (2025)/Linear Algebra for Game Development - Part 30

Linear Algebra for Game Development - Part 30

Author: Youngjin Kang Date: December 20, 2025

Before You Read

This article is Part 30 of the series, "Linear Algebra for Game Development". If you haven't, please read Part 1 first.

Crafting

In the previous few articles, we saw how a gameplay scenario can be modeled as a network of relations, as well as how to react to those relations based on some sort of distributed transaction system.

One major cornerstone of gameplay is still missing, though.

In this article, I would like to introduce the notion of synthesis - the idea that we are able to combine multiple objects (aka "items") and produce some kind of mixture out of them. In the language of game design, such a mechanic is often referred to as "crafting".

Linear Algebra for Game Development - Part 30 (Figure 1)

How will crafting work in the context of linear algebra? Before jumping directly into what vectors and matrices are capable of, let us first develop a bit of algebraic intuition in regard to the nature of combination.

I will begin with a simple example. Imagine that we have water and an empty cup. What happens when we combine the water with the empty cup? The answer is, they will result in a water-filled cup!

Linear Algebra for Game Development - Part 30 (Figure 2)

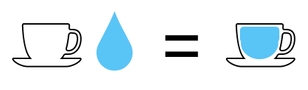
What if we combined blood instead of water? As you may have guessed, the result would be a blood-filled cup.

Linear Algebra for Game Development - Part 30 (Figure 3)

This leads us to imagine a plethora of fascinating use cases in the context of gameplay. Suppose that there is a dinner table, on top of which a pair of empty cups are placed.

Linear Algebra for Game Development - Part 30 (Figure 4)

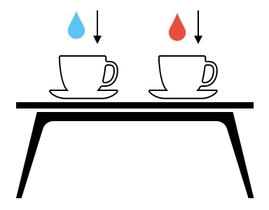
Here is the deal. Assume that, for whatever gameplay reason, we decided to pour water into the first cup and blood into the second cup. How shall we compute the results of these two combinations?

Linear Algebra for Game Development - Part 30 (Figure 5)

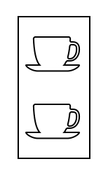
The very first thing to do, is to come up with a way of representing the current state of the game. Right now, we've got a pair of empty cups and nothing else. Therefore, we will simply create a column vector which consists of two entries, each of which is occupied by an empty cup.

Linear Algebra for Game Development - Part 30 (Figure 6)

As you may remember from the fundamentals of matrix algebra, we can obtain the the result of the first combination (between water and an empty cup) by means of a simple multiplication. Try multiplying our column vector by a row vector whose first element is water and second element is zero (i.e. nothing), and you will see that the result is a single water-filled cup.

Linear Algebra for Game Development - Part 30 (Figure 7)

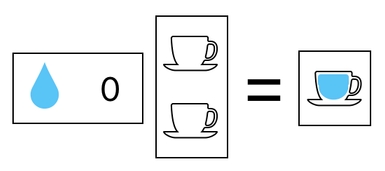
Similarly, you can try multiplying our column vector by a row vector whose first element is zero (i.e. nothing) and second element is blood, the consequence of which is a single blood-filled cup.

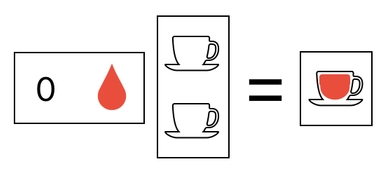
Linear Algebra for Game Development - Part 30 (Figure 8)

When you put these two multiplications together in a single matrix, both of the above results will show up simultaneously.

Linear Algebra for Game Development - Part 30 (Figure 9)

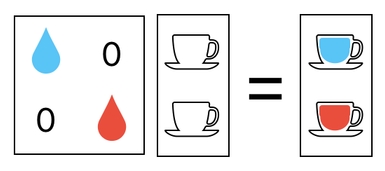
This, of course, is the same thing as having the first cup filled with water and the second cup filled with blood on our dinner table (which is the expected result).

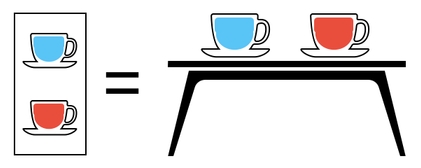
Linear Algebra for Game Development - Part 30 (Figure 10)

Enumeration

There is something fishy here, though. So far, our calculations have been relying on the assumption that a multiplication between an empty cup and water is equal to a water-filled cup, as well as that a multiplication between an empty cup and blood is equal to a blood-filled cup.

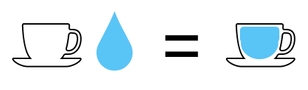
Linear Algebra for Game Development - Part 30 (Figure 11)

Linear Algebra for Game Development - Part 30 (Figure 12)

These two rules are pretty intuitive and easy to memorize, so we haven't experienced any major inconvenience yet.

Suppose, however, that the game designer happens to come up with hundreds or even thousands of crafting rules, many of which are not nearly as intuitive as the ones we just saw. What shall we do in such a case? Create a gigantic crafting table and make the system look it up whenever it needs to combine a pair of items?

While such an explicit lookup-based method will work for sure, there is a far more efficient (and elegant) approach.

The solution is to assign numbers to items, and represent each of their combinations as a straight up numerical multiplication. For example, we could just say that an empty cup is equal to 2, water is equal to 3, and blood is equal to 5.

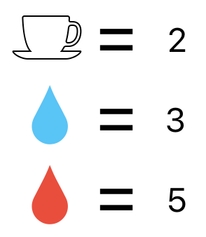
Linear Algebra for Game Development - Part 30 (Figure 13)

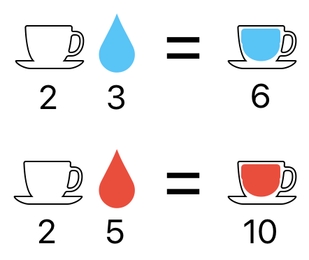
Taking a combination between water and an empty cup, then, will be the same thing as multiplying 2 by 3, which is equal to 6. And yes! This means that a water-filled cup must have the numerical value of 6. The same logic applies to the case of blood.

Linear Algebra for Game Development - Part 30 (Figure 14)

This kind of numerical encoding can be applied to a variety of unbounded imaginations. Suppose, for instance, that we are mixing water and blood. What happens when we do that?

Linear Algebra for Game Development - Part 30 (Figure 15)

Oh, for sure, the result will be a halfway mixture between water and blood, which may be called "diluted blood". And its numerical value will simply be equal to the product (i.e. result of multiplication) between the numerical value of water and the numerical value of blood.

And, what about when we take a combination between an empty cup and diluted blood? The answer is, we are going to get a cup filled with diluted blood. And its numerical value, of course, will be the product between that of the empty cup and that of the diluted blood.

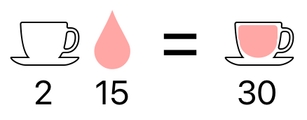
Linear Algebra for Game Development - Part 30 (Figure 16)

We can keep expanding our map of item-combinations like this; the only thing we need to do is encode each item with a unique number, whose value fits the pattern of multiplication in an appropriate manner. The rest of the crafting logic will be automatically handled by the nature of multiplication itself.

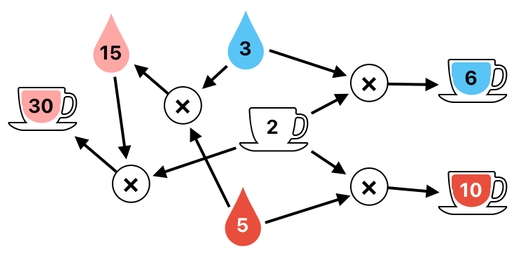
Linear Algebra for Game Development - Part 30 (Figure 17)

Decomposition

The next question is, what if we want to do the opposite - that is, split up a combination into its parts?

Imagine that we have a cup which is full of water. What do we have to do in order to make it empty again?

Linear Algebra for Game Development - Part 30 (Figure 18)

From an arithmetic point of view, one solution which quickly comes into mind is to divide the cup by water (because division is the inverse of multiplication). This will remove the water from the cup.

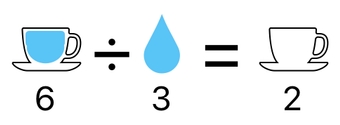
Linear Algebra for Game Development - Part 30 (Figure 19)

This method, however, is not something we can easily leverage in the context of linear algebra. Do you remember that, by means of matrix multiplication, we are able to manipulate multiple items simultaneously?

Linear Algebra for Game Development - Part 30 (Figure 20)

Only additions and multiplication are involved here, and in order to perform division, we will need to employ additional techniques (such as calculating the inverse of a matrix, etc).

Fortunately, there is a much simpler way to undo a process of combination. As you may recall from your basic knowledge in arithmetic, dividing by a number is the same thing as multiplying by its reciprocal (For example, dividing by N is the same thing as multiplying by 1/N).

This means that the process of removing water is the same thing as multiplying by the water's reciprocal.

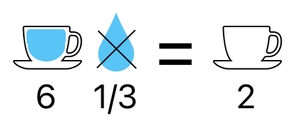
Linear Algebra for Game Development - Part 30 (Figure 21)

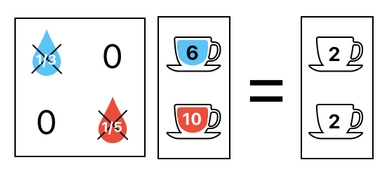
With this in mind, we are now able to split off individual items from their combinations. First of all, let me remind you that combining multiple items can be done by multiplying them with one another. This is demonstrated by the matrix multiplication shown here:

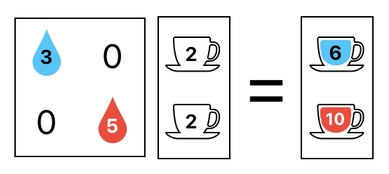
Linear Algebra for Game Development - Part 30 (Figure 22)

See? In this example, we are adding water to the first cup, while also adding blood to the second cup.

Here comes the challenge. What if we want to reverse these two processes? That is, what if we want to remove the water from the first cup and remove the blood from the second cup?

The solution is surprisingly simple. Instead of multiplying the cups by water (= 3) and blood (= 5), all we have to do is multiply the cups by the inverse of water (= 1/3) and inverse of blood (= 1/5). This will undo the combinations we have done, reverting the cups back to how they were before.

Linear Algebra for Game Development - Part 30 (Figure 23)

Conservation of Energy

The examples we have seen so far, though, do not conform to reality from a physical standpoint.

For the purpose of filling a cup with water, for instance, I just generated fresh new water out of nowhere and added it to the cup (which is pure magic).

Linear Algebra for Game Development - Part 30 (Figure 24)

In real life, we would have to bring water from somewhere else and pour it into the cup (i.e. energy must be conserved).

Linear Algebra for Game Development - Part 30 (Figure 25)

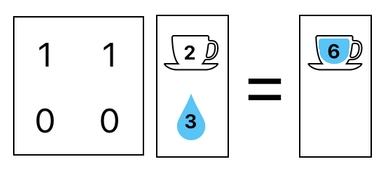
In order to ensure that energy is being conserved, we will first need to make sure that both the cup and water already exist in our world (i.e. They are listed as rows in our data table). Next, we will need to design our transaction matrix in a way which only allows it to relocate existing items from place to place; it must never be allowed to create new items or destroy existing items.

The following matrix operation, for example, moves the water into the cup without creating or destroying anything, thus preserving the total amount of energy (matter) in our game world.

Linear Algebra for Game Development - Part 30 (Figure 26)

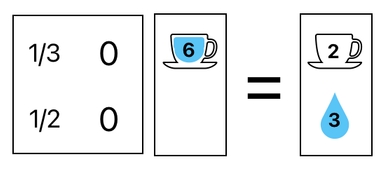
The inverse process, too, is bound to obey the same law. The following matrix operation shows how we can remove the water from the cup and put it back to where it was, without creating or destroying anything.

Linear Algebra for Game Development - Part 30 (Figure 27)