
Author: Youngjin Kang Date: January 23, 2025
How to measure the quality of a sandwich?
It really depends on one's personal taste, but we can still talk about some of the commonly available methodologies. Being able to evaluate the overall quality of a sandwich is a necessary skill to have, in order to become a legendary sandwich craftsman.

A truly appetizing sandwich must obey the following two principles:
(1) It consists of tasty ingredients.
(2) These ingredients are stacked in a tasty order.The word "tasty" may sound a bit too subjective, and indeed it is. However, it will appear to be far more sensible if you just interpret it as "generally tasty" or, in other words, "considered tasty by the average eater".
Let us begin with the first principle.
The first step toward the making of a highly edible sandwich is to gather ingredients which can be appreciated even when we eat each of them individually. This means that it is crucial for us to first evaluate the quality of each ingredient and assign a number to it (denoting its degree of tastiness). We may refer to this number as the ingredient's "taste score".
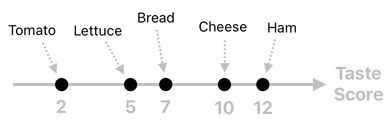
Since a sandwich is a combination of multiple ingredients, a straightforward way of judging its quality is to first evaluate the scores of its individual components and then sum them all up.
Let me start with a simple example. The following image is the anatomy of a cheese sandwich which was showcased before.
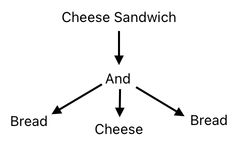
How to calculate its overall score? Oh, it may seem daunting at first, but the problem is not complicated at all as long as you put some thought to it. Let us first assign the appropriate score to each of the sandwich's ingredients, and then take the sum of them (denoted by the "+" sign).
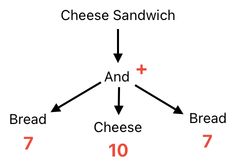
The result of such computation could be used to represent the overall taste score of the cheese sandwich. Why? Because a cheese sandwich is basically just the "sum" of its three constituents - lower bread, cheese, and upper bread. If we know their individual scores, therefore, it should make sense to assume that the score of the whole sandwich is their sum.
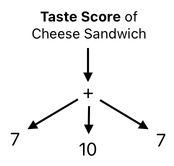
Assuming that the score of each piece of bread is 7 and the score of each slice of cheese is 10, we may conclude that the score of the cheese sandwich is 7 + 10 + 7 = 24.

All right, here is the next example. How shall we compute the taste score of a sausage sandwich?
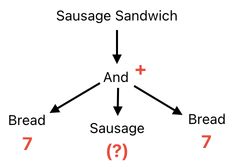
Here, we will assume that the sausage is an abstract item; that is, the word "sausage" is simply a generic term which is being used to indicate one of the 3 possible choices - chicken sausage, pork sausage, and beef sausage.
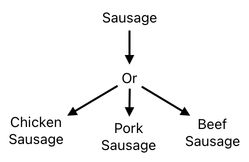
This means that, in order to figure out the taste score of the "sausage" part of the sandwich, we must first know how to determine the score of something uncertain (i.e. something which comes with multiple choices).
This too, however, is not a headache at all. Assuming that each choice has an equal chance of being picked up, we can claim from a statistical point of view that the most expected score of a randomly selected sausage is simply the average score of its 3 potential choices (i.e. chicken, pork, or beef).
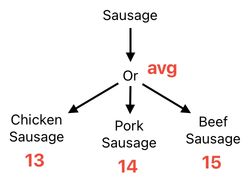
The term "avg" is just a shorthand for "average", by the way. If we suppose that the scores of the 3 aforementioned types of sausages are 13, 14, and 15, respectively, we will be able to conclude that the overall score of the "sausage" in our context is the average of 13, 14, and 15.
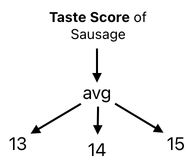
This score calculation procedure can substitute the "sausage" part of the sausage sandwich, yielding the following arithmetic scheme:
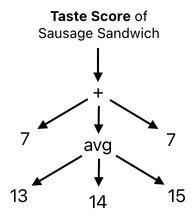
If we compute the "avg" part, we will get this:
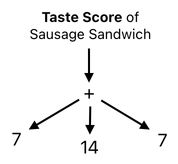
... which eventually simplifies down to a single number, representing the sausage sandwich's overall score (shown below).

Okay, you might have noticed that there is something fishy in here. It is the fact that, if we are to stick to the above methodology and refuse further elaboration on how scores are to be derived, we will soon be forced to reach the conclusion that a sandwich with more ingredients should score higher than those with fewer ingredients.
This, of course, is not desirable. Unless you are a mere glutton whose only interest is to eat as much as possible, you will agree that packing more ingredients does not necessarily yield a better sandwich.
Let us take a cheese sandwich as an example. We know that it has a single slice of cheese in it, so it makes sense to simply add the score of the cheese to the sandwich's total score.
Since cheese is a highly favored ingredient (because it is tasty), let us add an additional slice of cheese to the sandwich and make it a "double-cheese sandwich".
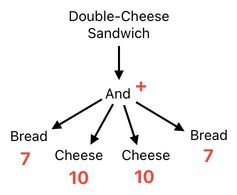
If we are to follow the scoring method established so far, we will have to say that adding this additional slice of cheese will basically double the cheese-score of the sandwich. This feels a bit excessive, but, let us move on anyways.
Next, I will try adding yet another slice of cheese to this double-cheese sandwich and turn it into a "triple-cheese sandwich". What will the new score be?
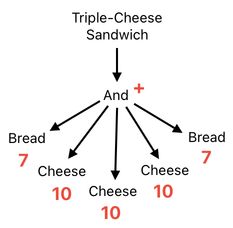
Of course, it will be even higher than that of the double-cheese sandwich, simply because there are more slices of cheese in this case.
The problem with this approach is that it just keeps incrementing the score as we add more and more ingredients.
What if we put 4 slices of cheese instead of 3? What about 5, 6, 7, or even 100 slices of cheese? Should a hundred-cheese sandwich score about 100 times higher than a single-cheese sandwich? Probably not. No one wants to eat a sandwich with a hundred slices of cheese in it.
Therefore, a mere summation of the individual ingredient scores does not accurately reflect the sandwich's overall score.
So, what's the solution? First off, we definitely need a better way to tell how good a sandwich is. Let us revisit the previous cheese sandwich example.

Just by looking at the ingredients, I am able to tell that it should score pretty high because it has cheese in it, yet not "too" high because it has cheese only and nothing else. A slice of ham would have made it a lot more appetizing.
But the question is, will this sandwich become more appetizing if I add a totally random thing as an extra ingredient, such as apple jam?
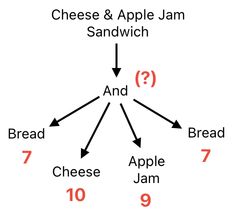
In my opinion, both a "cheese sandwich" and an "apple jam sandwich" deserve high scores, while a sandwich which contains both cheese AND apple jam in it does not.
The reason behind this is that cheese and apple jam usually do not pair up well. Some people might find it particularly attractive, but I do not believe that such appetite is commonplace (Consider "mint chocolate" as an example).
The main problem here is that when two things are combined, their values do not necessarily add up. Depending on how harmonious they are when put together, they may introduce either synergy or dissonance.
Take a look at the following example here, which shows the anatomy of a PB&J (Peanut Butter & Jelly) sandwich.
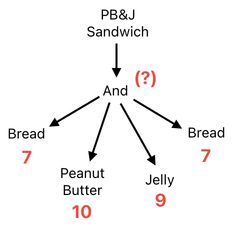
Compare this with the "cheese & apple jam sandwich" we saw before. If you are equipped with a decent sense of taste, you should probably agree that the PB&J sandwich deserves a much higher score than the other one. Peanut butter and jelly is a way better choice of combination than the one between cheese and apple jam.
This sort of reasoning leads us to the conclusion that, when evaluating a sandwich, we must take into account not only the scores of the individual ingredients, but also the scores of their relations.
Here is an alternative scoring method.
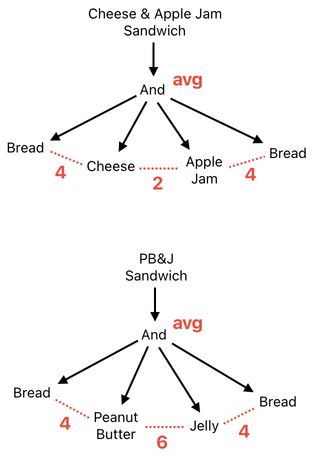
As you can tell from the pictures above, I am now assigning scores to pairs of neighboring items, not the items themselves (Notice that the pairing of peanut butter and jelly produces a higher score than that of cheese and apple jam). Then, I am simply taking their average to obtain the overall score of the sandwich.
This, too, has its own flaws. For instance, it does not consider cases in which we are duplicating the same thing a bunch of times (e.g. 100 cheese slices).
Nevertheless, what is shown above is an improvement over the previous methodology, and we are free to keep rectifying it. For now, though, I will pause here and move on to other important topics.
(Will be continued in Chapter 4)
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service