
Author: Youngjin Kang Date: October 31, 2023
(Continued from volume 8)
As long as we suppose that an idea is a set of coordinate value specifications inside the space of all conceivable ideas, we have the authority to tell that any idea can be modelled as a vector wherein each element is either an unbounded variable or a constant.
The "idea of idea" is the ultimate root of all other ideas. It represents the whole volume of the idea space, and is indicated by a vector which is unbounded in every direction.
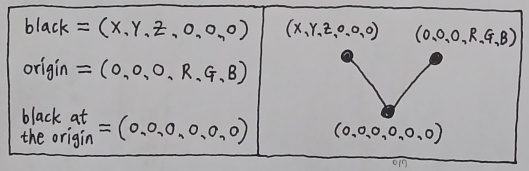
The idea of "black" is basically the RGB value of (0, 0, 0). If we assume that the idea space comprises only two distinct quantities called "position" (X, Y, Z) and "color" (R, G, B), as well as that they are juxtaposed under the format: (X, Y, Z, R, G, B), "black" will be formulated as the vector: (X, Y, Z, 0, 0, 0). Here, (X, Y, Z) are variables and (0, 0, 0) are constants.
Similarly, the idea of the origin (center) of our physical space, since it can be written as the XYZ value of (0, 0, 0), will be rendered as the vector: (0, 0, 0, R, G, B). Here, (0, 0, 0) are constants and (R, G, B) are variables.
For the sake of visual simplicity, let me fancy for now that the idea space is just a 2D vector space with only two scalar components: color and position.
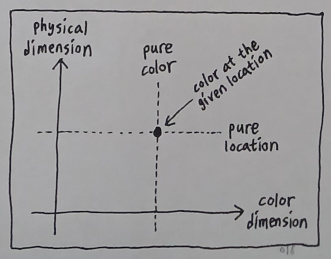
In this experimental scenario, the idea "black" only possesses a fixed color value and does not care about its position because a color can potentially appear anywhere in space. Therefore, such an idea is a line which spans the entire spatial axis and confines itself to a single color.
On the other hand, the idea of "the origin" only possesses a fixed position and does not care about its color because a point in space does not require any chromatic attribute to describe itself. Therefore, such an idea is a line which spans the entire chromatic axis while sticking itself to a single physical spot.
And the point of intersection between these two lines is the idea which represents the existence of the given color at the given location, due to the fact that its chromatic and locational elements are both fully specified. It is an instance of coincidence between the two dimensions of qualia.
From a computational standpoint, one may as well say that the conception of the aforementioned coincidence is functionally analogous to a logical operator which receives a pair of vectors as its parameters and outputs a new vector which is the result of collapsing some of their infinite numerical ranges down to pinpoint quantities (constants). The reason behind this is pretty simple; if you have an unknown variable called X and a statement which says that X is equal to 0, your conclusion will obviously be that any instance of X can be replaced with 0.
Reduction of dimensions through geometric intersection, however, is not the only type of coincidence demonstrated in our previous "cats and dogs" example. We also have coincidences which increment the number of dimensions by means of generalization which, instead of discovering the intersection between two geometric volumes, creates a brand new volume which contains both of them.
Imagine that we are living in a 9-dimensional idea space, wherein each idea consists of 3 physical dimensions (X, Y, Z), 3 chromatic dimensions (R, G, B), and 3 structural dimensions (S1, S2, S3).
And let us further suppose that, for ease of graphical illustration, we are plotting such ideas inside a hypothetical 3D space made up of three virtual dimensions: A single physical axis which substitutes the X, Y, Z values, a single color axis which substitutes the R, G, B values, and a single structural axis which substitutes the S1, S2, S3 values.
If we declare that:
(1) In the color dimension, 0 means black and 1 means white.
(2) In the structural dimension, 0 means cat and 1 means dog.
Then this will subsequently lead us to the following conclusions:
(1) The idea of "black" is a plane crossing every point in space which satisfies the condition: "color = 0".
(2) The idea of "cat" is a plane crossing every point in space which satisfies the condition: "structure = 0".
(3) The idea of "black cat" is a line crossing every point in space which satisfies the two conditions: "color = 0, structure = 0".
(4) The idea of "black dog" is a line crossing every point in space which satisfies the two conditions: "color = 0, structure = 1".
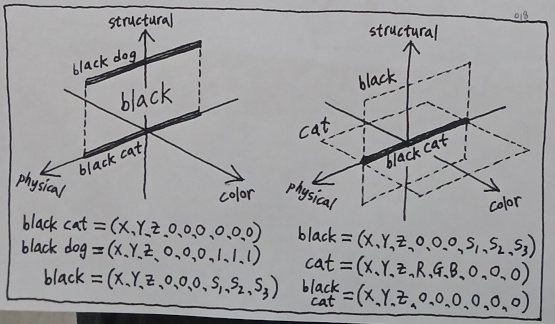
The so-called "coincidences" which were rather clumsily depicted before are now fully explicable in terms of geometric operations. The process of generalization (e.g. "black cat" and "black dog" being abstracted out into a generic class called "black") is equivalent to the creation of the smallest volume which contains both of the given volumes, and the process of specification (e.g. "black" and "cat" being synthesized into a specific object called "black cat") is equivalent to the identification of the intersection between the given volumes.

Numerically speaking, I may as well propose that generalization is the same thing as resolving the mismatch between two constants by turning them into a variable, whereas specification is the same thing as discarding a variable under the presence of a constant.
(Will be continued in volume 10)
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service