
Author: Youngjin Kang Date: November 18, 2023
(Continued from volume 14)
A digital computer is an elegant reality simulator; its internal state is a long sequence of 0s and 1s, wherein 0 could be interpreted as "emptiness" and 1 could be interpreted as "fullness".
Each binary digit (aka "bit") is an instance of the idea of space because it is capable of disclosing either 0 (emptiness) or 1 (fullness) in a fairly stochastic manner once we observe it. And as demonstrated in the prior volume, the availability of two or more of such instances (aka "positions") must be presumed as long as we decide to create a composition between either (1) emptiness and space, or (2) fullness and space.
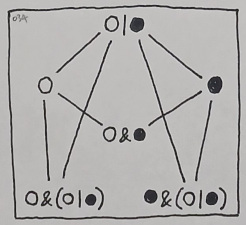
A technical implication of this should be best expressed in the context of a state machine. Suppose that the mind of any conscious being is just a single FSM (Finite State Machine) which comprises two states that may be referred to as "feeling emptiness" and "feeling fullness", such that whenever it feels emptiness, its mental state belongs to the former, and whenever it feels fullness, its mental state belongs to the latter.
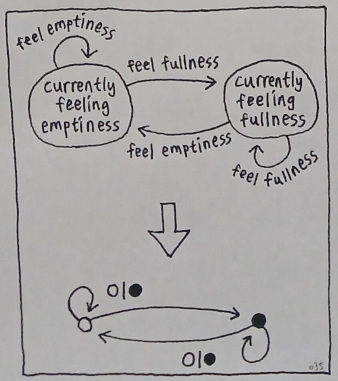
While feeling emptiness, we know that emptiness is definitely present in our mind, as well as that such a state of cognition can either stay in emptiness or transition into fullness. And while feeling fullness, we know that fullness is definitely present in our mind, as well as that such a state of cognition can either stay in fullness or transition into emptiness.
The idea of "emptiness AND space" (as well as "fullness AND space"), therefore, can be thought of as a combination between the current state (i.e. left side of the AND relation) and its possible set of transitions (i.e. right side of the AND relation).
The state diagram above can easily be imagined as a succinct depiction of a physical realm which consists of a network of spatial locations, each of which is either empty or full. The aforementioned state machine (i.e. the observer) would then be a spectator which traverses such points in space whilst perceiving only one of them at a given moment.
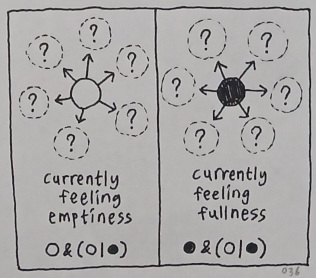
This is not the end of the story, for sure. You know that our senses are not so binary on a macroscopic level; they are oftentimes grayscale in appearance.
In order to be able to handle such fine-grained differences, we must realize that this is what introduces dimensions to our system of quantitative reasoning. We need a dimension to represent a spectrum of senses rather than just a simple dichotomy. The question is, what are dimensions made out of?
One thing to note is that they do not necessarily differ from the concepts we have hitherto been witnessing on a fundamental level. As long as we allow a dimension to have any finite range and resolution, we may imagine that a pair of values (i.e. a dyad) is the simplest kind of dimension one can ever conceive.
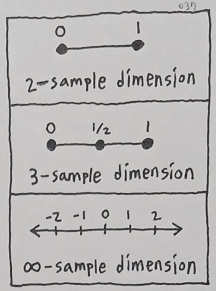
Since a dimension is a carrier of differences, a single value (i.e. sample point) cannot identify itself as a dimension. A pair of values, on the other hand, qualifies as one because it involves the concept of differentiation. As we add more values, we see that its axis gets more and more granular.
But how does this process of "adding more values" occur, exactly? A breeze of intuition lets me just draw a line on a sheet of paper and keep dividing it into smaller and smaller segments, thereby "proving" that it is possible to come up with a dimension and increase its resolution to whichever degree we desire. However, it is such a clumsy way of defining what a dimension really is from a meta-mathematical point of view.
A more logical method is to resort back to the pattern of abstraction/composition and start building from there. We have already seen that the idea of "form" is a mixture between one instance of emptiness and one instance of fullness, without any suggestion of one of them being greater than the other in terms of their ratio.
The thing is, nothing really stops us from combining the idea of form itself (i.e. emptiness AND fullness) with pure emptiness, in which case we get "emptiness AND (emptiness AND fullness)" as the product. It consists of 2 instances of emptiness and 1 instance of fullness, just like a water molecule consists of 2 hydrogen atoms and 1 oxygen atom.
The same exact pattern applies to the case of fullness, in which we have "fullness AND (emptiness AND fullness)" - the combination between 2 instances of fullness and 1 instance of emptiness.
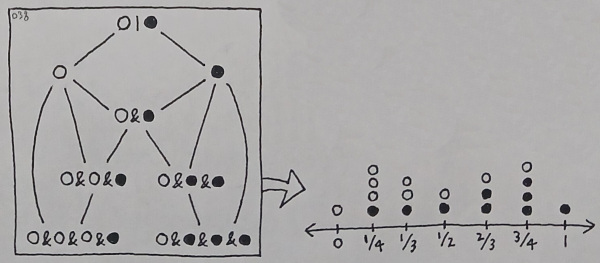
This sort of formulation can repeat itself in a recursive manner, from which any fraction of two positive integers is able to emerge as a ratio between the two binary components. As we gather such fractions and line them up in an ordered sequence (under the guidance of some "ordering law"), we see that such a construct qualifies as the axis of a dimension.
This reveals that a "dimension" can be defined as a rule under which a set of ideas can be arranged in a strictly ascending (or descending) order. In our particular case, it is based upon the ratio between the number of instances of emptiness and the number of instances of fullness.
(Will be continued in volume 16)
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service