
Author: Youngjin Kang Date: 2023.03
(Continued from Volume 8)
So far, we have been encountering the difficulty of representing not only the mechanics but also the narratives of the game in a computationally interpretable form. Since a game is a fairly sophisticated architecture made up of both mechanics and narratives which constantly reinforce each other in an interactive way, it is crucial to ensure that we are able to formulate a unified language upon which both of these two opposing faculties of knowledge can collaborate together as a whole.
The main struggle with the attempts to represent the game's narratives in a purely mathematical (thus translatable to mechanics) format belongs to their apparent image of vagueness. They often involve emotional components such as joy, sorrow, jealousy, remorse, enlightenment, and many others, as well as personalities, beliefs, worldviews, senses that are either observed or not observed, thoughts that are either conceived or not conceived, and so on.
Such a vast field of complexity, in general, tends to compel the designer to develop the narrative elements of the game in a rather experimental manner for the purpose of avoiding ungrounded speculations, which derives the basis of its reasoning from the engagement of the player on a cognitive level and measures the relative degree of success of each design approach in terms of its most directly measurable outcomes such as the intensity and time of engagement.
It may also be argued, however, that such a cognition-centered methodology has widely been practiced by AAA game companies and other large institutions which are armed with countless experts in the area of manipulative psychology (whom a small group of independent developers can hardly compete with). If one is to undertake a journey of becoming an indie developer, therefore, being able to design a game whose degree of competence in the marketplace lies on a distinct dimension of measurement that is somehow differentiable from the brute-force power of dopamine addiction is more or less a pragmatic necessity.
For this reason, a design process that is of any considerable value in this oversaturated industry ought to possess some form of metaphysical insight which goes deeper into the fundamental nature of narratives and mechanics themselves, rather than focusing on the outer surface of their cognitive effects.
Such an insight should not be confused with the so-called "artistic endeavors", however, which are carelessly coined by amateurs who feign the integrity of their imagination based upon the mere ambiguity of the way in which they associate their ideas. Such an undisciplined sort of self-expression, which bases its value on the aesthetics of one's own fashionable ego, usually does not lead to the proof of its uniqueness because there are way too many of them who desperately clamor in unison to let the rest of the world know how "creative" they are.
If we are rationally minded individuals who make decisions out of some form of logic rather than an amorphous cloud of emotional impulses, it should not be an overstatement to say that an attempt to design a game that is commercially viable yet still distinguishes itself from the most common niche of today's game industry (which is highly empirical in nature) should begin with the imaginative power of pure mathematics as well as its philosophical origin - for it is an intuitively fitting notion that a body of a priori knowledge which excludes mathematics from its domain of reasoning easily veers towards an abyss of vagueness and thus disrupts the game's structural integrity.
And in order for such a line of reasoning to invariably apply to the full process of game development, we ought to make sure that both the narratives and mechanics of the gameplay, as well as their back-and-forth interactions, are representable in terms of mathematical entities.
In the last volume, we witnessed the difficulty of defining and measuring volitional (psychological) forces of gameplay agents as opposed to forces which solely belong to the domain of pure mechanics (e.g. motion, heat, gravity, chemical reactions, etc). Such a challenge seemed to suggest at first that drawing the complete anatomy of narrative elements in a system-oriented manner is an impossible task, but later on we also saw that they do not necessarily have to differ from mechanics on a fundamental level. The reason behind this bold statement of wholeness lies on the notion that, in the vast majority of cases, narratives stem from motivations and motivations stem from the idea of energy exchange.

One might argue that some of the sources of narratives such as purely abstract emotions have nothing to do with the concept of "energy", yet such a statement can be considered valid only if we suppose that the word "energy" always refers to its conventional use cases such as generation/consumption of electricity, petroleum, foods, and other physical entities.
Since energy is something that is defined in terms of a causal relation among observations (i.e. An underlying pattern of nature which causes a group of observations at one point in time to be associated with another group of observations at a different point in time) instead of the sense-data of individual observations themselves, we may claim that any observable phenomenon which bears a hint of such a relation can be assumed to involve some form of energy transfer. And as far as I can tell, there has not been a decisive reason to assume that such causal phenomena must be confined to those which are considered physical, as opposed to those which are considered mental.
The energy-oriented reasoning leads us to the idea that not only mechanical but also narrative elements of gameplay are capable of being defined in the form of energy exchange, as long as we do not limit the scope of our definition of the term "energy" to those which pertain to the study of physics.
As we all know, there are different kinds of energy such as those that are gravitational, electrical, thermal, nuclear, and so forth. This makes it quite logically sound to say that it is okay for us to expand this collection of energy types by adding new ones to it in order to fit our design purposes, especially because what we are designing is a fictional universe in which the very definition of "real" as opposed to "unreal" is more or less arbitrary. For example, it is perfectly sensical to imagine abstract forms of energy such as "emotional energy", "financial energy" (i.e. monetary value), and many others which have the ability to modify the state of causality of the system.
Time, too, can be interpreted as a form of energy, and one may fancy that any object which is willing to change its current location does so by spending its time-energy (because it takes time for an object to move, unless it is capable of instantaneous teleportation). This backs up my previous claim that a distance in space can be measured in terms of the amount of energy spent by an object while it travels from one point to another; even in case where there is absolutely no force field (e.g. gravity) or medium of friction (e.g. air) surrounding the object, which would let it simply move through the continuum of space based upon its own inertia without requiring any change in its potential/kinetic forms of energy, it is still bound to consume a certain number of time-energy particles for every unit distance it travels.
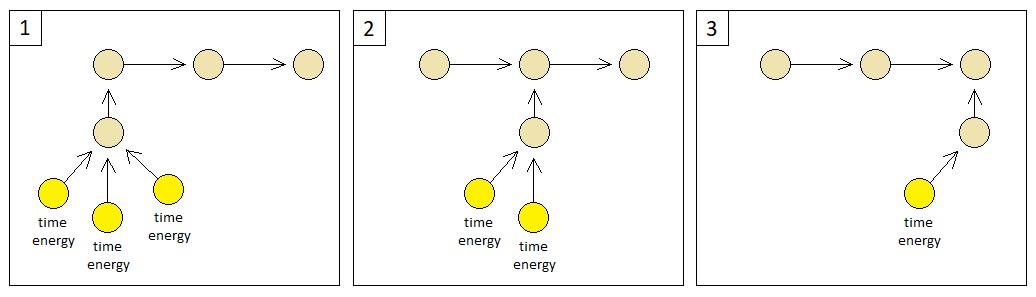
How to determine the rules of exchange among energy particles, then? For this question, I would say that it is generally fine to presume that abstract types of energy which belong to the domain of psychological interactions follow the same exact rules as the ones that are obeyed by physical types (because I have not yet perceived a case in which such a supposition should be considered logically contradictory).
In the last volume, I suggested the feasibility of the existence of what is called a "potential". A potential is essentially an indivisible container which may or may not have an energy atom bound to itself; it possesses the ability to receive, store, and emit an energy atom of a specific type which might pertain to the interests of the observer, without necessarily letting the observer know whether or not it is currently available.
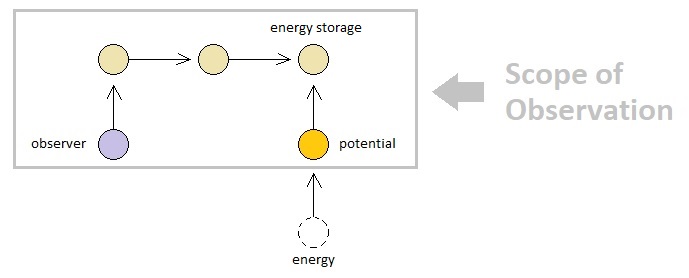
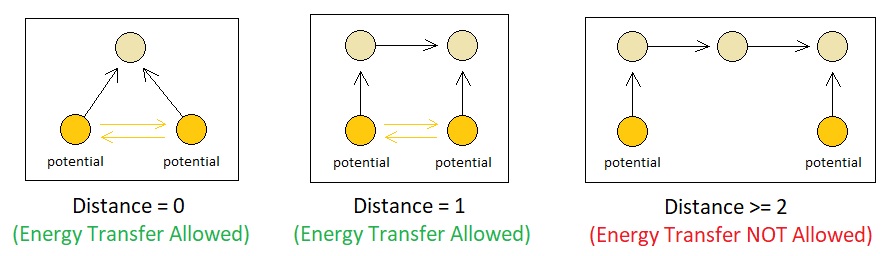
When there are two potentials that are sufficiently close to each other (i.e. separated by at most 1 binding), one may expect energy atoms to travel from one potential to the other. In order to specify the direction of energy transfer without devising truckloads of arbitrary rules, however, we need to understand the concept of energy levels.
There are different levels in each type of energy. Gravitational energy, for example, has its energy levels allocated to different altitudes of space with respect to the center of the Earth. When a ball gets lifted up into the sky, its gravitational energy level increases (because the altitude is higher). And when it falls down to the ground, its gravitational energy level decreases (because the altitude is lower). Therefore, it makes sense for us to say that the ball is an energy atom which belongs to either a potential which is located at the ground or a potential which is located at the sky depending on how far away it is from the center of the Earth. Hence it is also sensible to state, due to the apparent nature of gravity which we all agree upon, that such an energy atom has a tendency of always moving towards a lower energy level than the current one to which it belongs, as long as there is no counteracting force which prevents it.
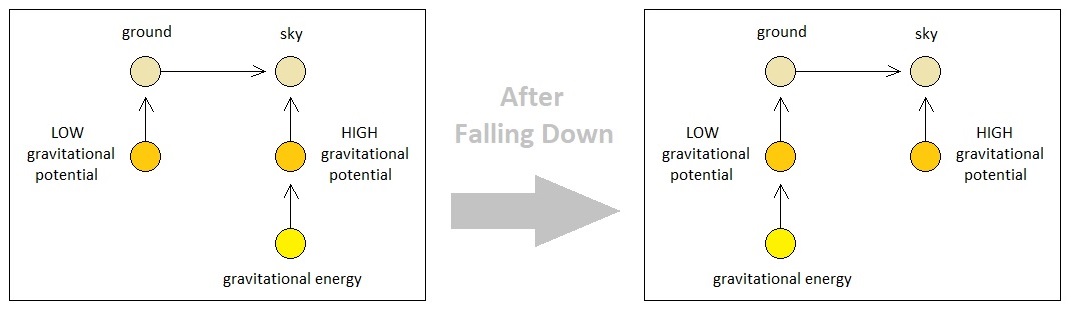
This tendency is universally present in all energy types. Electrical charges move from higher to lower electrical energy levels (which allows us to run electric circuits), and heat moves from higher to lower thermal energy levels which results in eventual thermal equilibrium. Abstract units of energy (e.g. time), too, have their own levels allocated to various points in spacetime, across which they travel in the descending order.
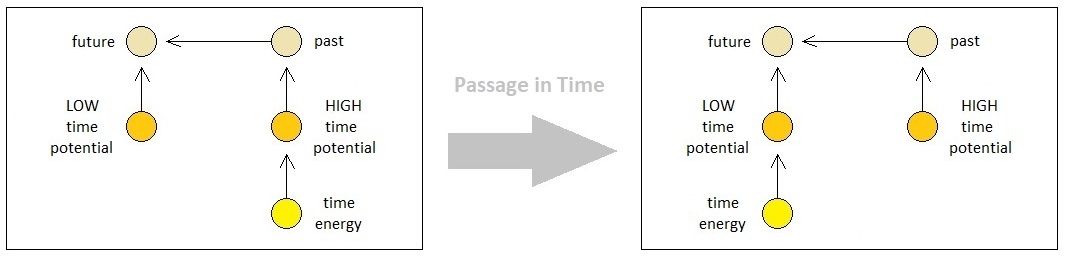
If we let each potential have its own energy level, therefore, it will be reasonable to claim that an energy atom which is bound to a potential of level N will automatically rebind itself to any other potential of level X (where X < N) which is at most 1 binding apart from the level-N potential.
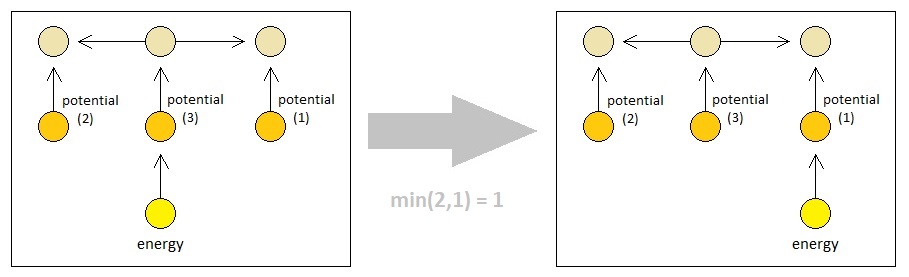
Also, our observations in gravitational phenomena tell us that an agent of an energy field always follows the shortest route in terms of reducing its own energy level. That is, an uninterrupted ball always falls directly towards the center of the Earth because it is the line of displacement which guarantees the highest rate of reduction in its gravitational energy level. Thus, we can conclude that an energy atom which is bound to a level-N potential always automatically rebinds itself to any other adjacent potential of level X which satisfies both of the following conditions:
(1) X < N
(2) X is the smallest of the levels of all potentials that are adjacent to the aforementioned level-N potential.
(Note: "Adjacent" means that two potentials are separated by at most 1 atomic binding.)
One question which may arise is, "What happens after all energy atoms reach their lowest possible energy levels? Won't this stall the entire system because there will no longer be any transfer of energy?" And this doubt is perfectly reasonable because it should indeed be the case if only the pattern stated above constitutes the dynamics of the gameplay system. Eventually, all energy atoms will settle down in their ultimate state of equilibrium and no more event will happen thereafter; this is a theoretical analogue of the so-called "heat death" of our universe.
Let us note, however, that our game world does not have to be a completely closed system. We may assume the existence of external forces which revive dead energy particles (i.e. those which have fallen to their lowest possible levels) by sending them back to their highest levels by means of two special kinds of potentials - sinks and sources.
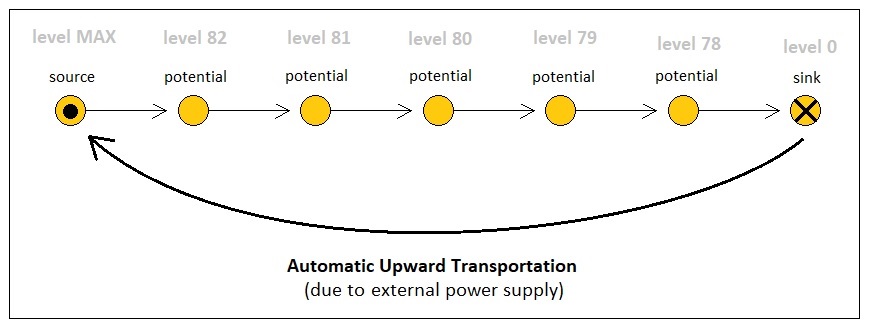
A sink is a potential which has the lowest possible energy level, whereas a source is a potential which has the highest possible energy level. A sink follows a special way of energy transfer which differs from that of all other potentials - that is, an energy atom which enters a sink always instantly gets transported to one of the sources which exist within the gameplay world, despite the fact that a source's energy level is higher than that of a sink. This scheme may sound contradictory to our reasoning of the direction in which energy is always bound to propagate (i.e. from high potential to low potential), yet the logic makes perfect sense if we assume that there is an external power supply which constantly provides a stream of force which "recharges" the most exhausted energy particles back to their most excited state. We can think of a sink and a source as the two ends of a battery in an electric circuit.
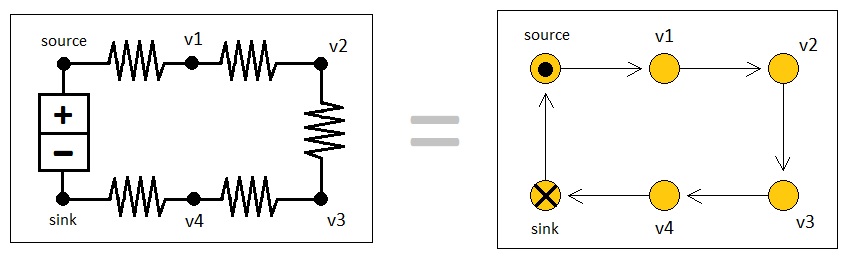
So, with the presence of potentials and their recycling mechanism, we now have a system which is able to maintain its own perpetual cycle of dynamic events. Energy atoms flow from upstream to downstream inside the vast network of potentials, more or less periodically circulating back to the top of the upstream with the aid of sinks/sources.
However, a game is something more than just a physics simulation and is therefore required to support the emergence of active agents and their motive-driven energy exchanges. The reason behind this is that gameplay begins with the conceptual division between the self and the rest of the world. Both the player and NPCs are decision-making entities (e.g. biological organisms) as opposed to rudimentary mechanical bodies which only react to impulses on a short-term case by case basis, and such a hint of inner complexity can be realized by separating out each character's inventory of energy particles from those which belong to the outside of its own body. Under this hypothetical division, we can easily imagine that an active gameplay agent's own set of goals and actions directly correlate to instances of direct energy transfer which occur between the inside and outside of the agent's existential boundary, each of which can be defined as a constituent of an exchange of energy particles (aka "transaction").
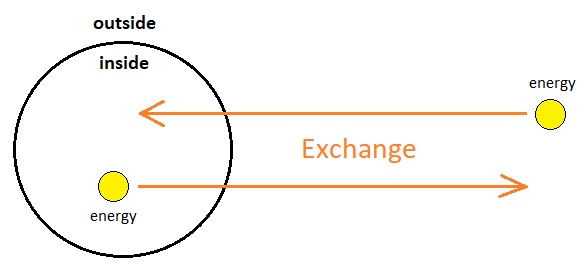
The concept of exchange is trickier to define than mere flux of energy from high to low potentials, due to its nature of bidirectionality and simultaneity. And for this reason, we must take extra precautions not to convolute our definitions too much while constructing the mathematical foundation of what an exchange is.
Let us first consider the mechanic of autonomous movement as an example. An organism (such as an animal) moves itself by giving off one of its kinetic energy atoms and receiving a chance to modify its current position in return. This is probably the most basic yet also the most significant type of exchange due to the fact that a movement is the most fundamental unit of action one can ever imagine (as explained in volume 2).
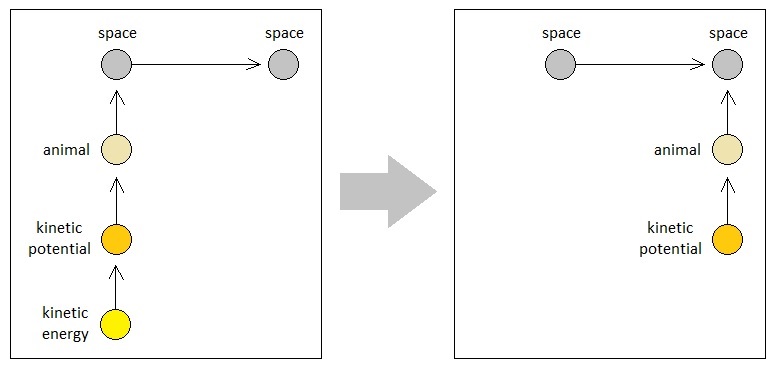
First of all, it is not hard to guess that the consumption of kinetic energy can be explained as an event in which a kinetic energy atom transfers itself from a relatively high kinetic potential to a relatively low kinetic potential, given that a condition which allows the occurrence of such an event is present. If we apply this same exact mode of interpretation to the phenomenon of locomotion, we should be able to hypothesize that the organism (i.e. subject of motion) itself can be imagined as an energy atom, and that its present and future spatial locations can be imagined as having potentials in them that are capable of transmitting energy.
Supposing that there is a special type of energy called "locomotive energy", one may fancy that a voluntary mover's initial location of movement temporarily becomes an owner of a high-level locomotive potential, while its final location of movement temporarily becomes an owner of a low-level locomotive potential, and that the moving agent itself is a locomotive energy particle which follows the stream of locomotive potentials in the most rapidly descending order. Meanwhile, it should also be assumed that the mover temporarily becomes an owner of a kinetic sink in order to dissipate one of its kinetic energy particles while moving.
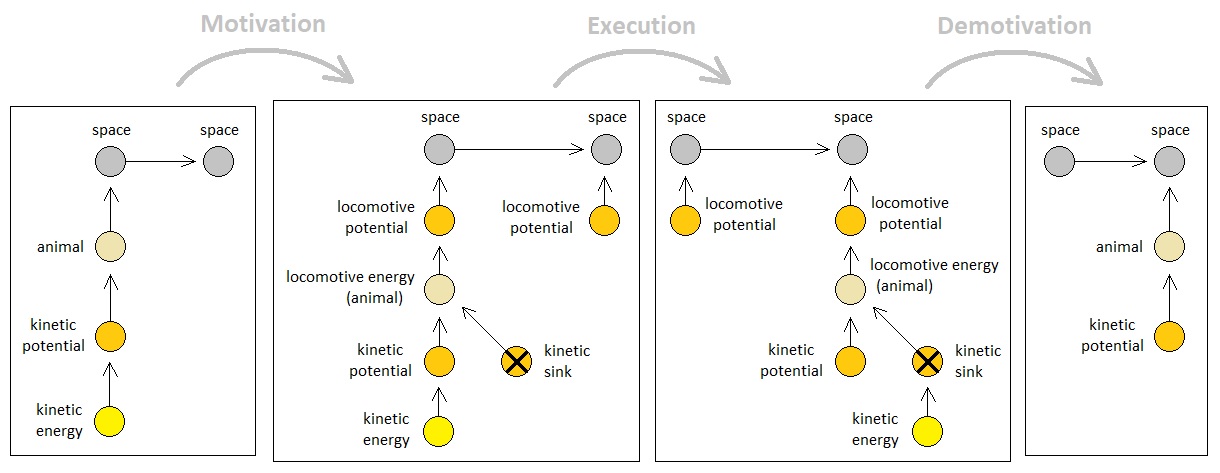
Since a voluntary movement is not something which occurs naturally without any psychological determination, it must be triggered by a process of motivation. In our hypothetical model, this phenomenon can be interpreted as a temporary addition of a set of atoms to the system, which immediately get taken back as soon as they invoke the desired action.
This is how a simultaneous exchange of energy particles is able to take place within the context of an autonomous agent and its surrounding environment. The agent motivates itself (i.e. adds a specific set of potentials to the scene), follows its own motivation (i.e. waits for a moment to let the energy atoms transfer themselves to lower potentials), and then terminates its own motivation (i.e. removes the potentials it just added). The end result of this 3-step process is an exchange between 1 outgoing kinetic energy atom and 1 incoming locomotive energy atom, which is reminiscent of exchanging one currency with another inside a bank.
In the next volume, we will delve into the nature of exchange in more detail.
(Will be continued in Volume 10)
Previous Page Next Page
© 2019-2025 ThingsPool. All rights reserved.
Privacy Policy Terms of Service