
Author: Youngjin Kang Date: 2023.02
(Continued from Volume 1)
In the previous volume, I supposed a number of hypothetical elements which could be considered the most fundamental building blocks of any game we can possibly imagine. This may be deemed too rash an assumption, and I by no means deny the possibility that the conceptual model I have devised so far is a flawed one. In order to solve the problem of game design with reason rather than a cloud of irrational ideas, however, one should attempt to at least capture a rough snapshot of the abstract nature of games by means of bold generalization. It is my personal conviction that, as long as such generalization does not stray too far from our shared definition of adequacy, it may show us a pathway to a deeper understanding of how a game can be designed.
Let me recapitulate some of the main propositions that were previously made. A game, regardless of its genre, usually takes place in its own isolated world (unless we are designing an AR (Augmented Reality) game, in which case the world may have direct causal relations with that of our own). Inside this virtual world, we have a set of objects which interact with one another based upon certain rules. The question is, how many types of object should there be, and how should such types differ from each other? One might suppose that every one of these objects is merely a point mass which behaves solely according to the laws of classical mechanics, and this is a perfectly reasonable presupposition to make if we are designing a physics simulator. When we are designing a game, however, we must be aware of its narratives and how well they will be able to articulate themselves on top of our model of how objects are distinguished and arranged within the context of gameplay.
In order not to deviate from such a task, I first rooted the origin of my design belief in the existence of a lifeform as a purely mathematical entity and the notion that its ultimate goal is to survive and reproduce for the purpose of prolonging its own existence as much as possible - for it is the question of life and death (i.e. "being" vs "non-being") which sits on the heart of any narrative, since narratives themselves are issued by living beings. And to clearly define the full range of dynamics which signify the presence of life and its spectrum of primeval goals, I have come up with a number of spatial entities.
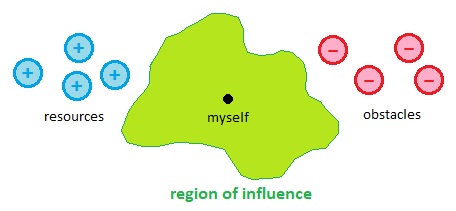
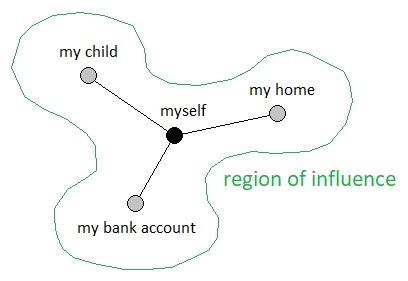
Inside the game world, there is a point in space which represents the central lifeform called "myself". This is the protagonist which is supposed to be the focal point of the game's narratives. This biological organism, for the purpose of following its instincts (e.g. live, eat, grow, reproduce) as accurately as possible, has developed a tendency to measure its own success with respect to the rest of the universe by means of its own "region of influence". When the region grows in size, the organism knows that the footprint of its own existence will propagate further through spacetime and therefore satisfy its ultimate purpose in life. When the region shrinks in size, on the other hand, the organism knows that the distance of such propagation will be shortened (which is clearly undesirable).
Aside from the presence of a lifeform and its surrounding region of influence, there are two opposing types of particles called "resources" and "obstacles". Colliding with a resource increments the lifeform's number of chances of executing an action, thereby enabling it to grow its region of influence in larger quantities than before. Colliding with an obstacle decrements the lifeform's number of chances of executing an action, thereby forcing it to grow its region of influence in smaller quantities than before.
All these theoretical objects and their relations collectively form a pattern language of the game's narratives, not from a set of vague emotional/cultural references, but from a fixed set of mathematical definitions. For example, the modeling I have done so far allows me to summarize the aforementioned phenomena in terms of 3 independent variables (illustrated below).
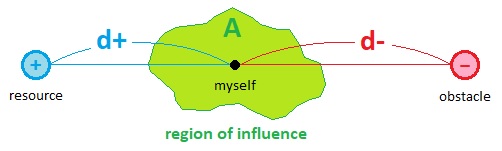
In this diagram, "A" denotes the area of the protagonist's region of influence, "d+" denotes the average distance between the protagonist and the resources which it is able to observe (either via sensory organs or memory), and "d-" denotes the average distance between the protagonist and the obstacles which it is able to observe (either via sensory organs or memory).
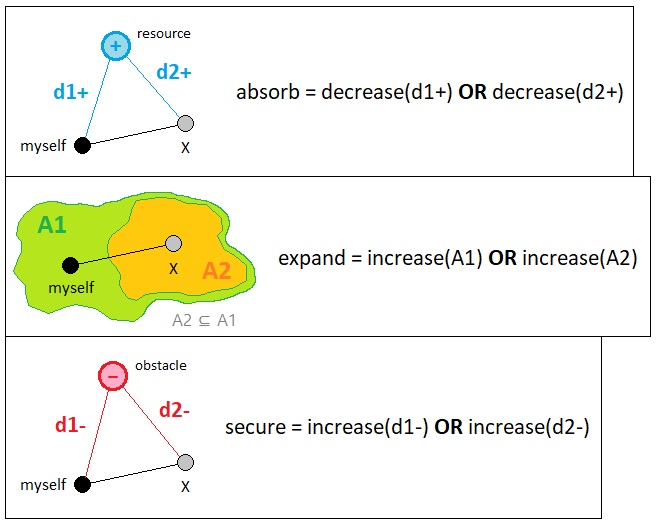
Previously, I have suggested the existence of the three most fundamental goals of every living entity: (1) Absorb, (2) Expand, and (3) Secure. The reasoning behind the conception of these three becomes clearer when we consider them as the simplest collection of motives in terms of the derivatives of the protagonist's three scalar variables: (1) "d+", (2) "A", and (3) "d-".
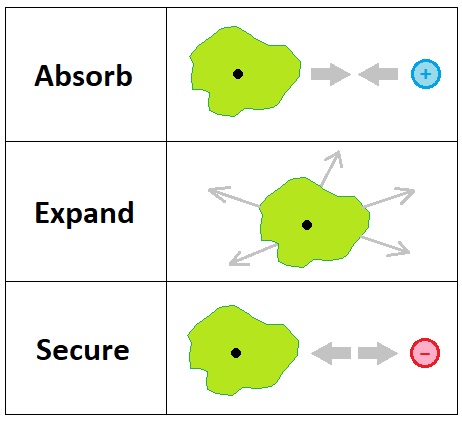
To "absorb" is to decrease the distance between myself and a nearby resource, so as to grab it, eat it, and digest it for the purpose of gaining nutrients. This lets me carry out a greater number of actions than before due to increased energy. To "expand" is to enlarge the area of my region of influence, which is done by visiting points in space that are external to myself or by creating offsprings that are capable of visiting such places instead. To "secure" is to increase the distance between myself and a nearby obstacle, so as to decrease the number of chances of having my own energy taken away by it.
These definitions can nicely be summarized into 3 algebraic expressions, which are listed below.
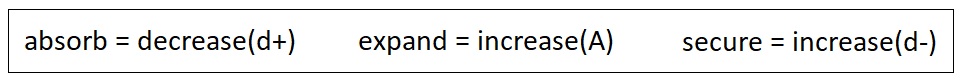
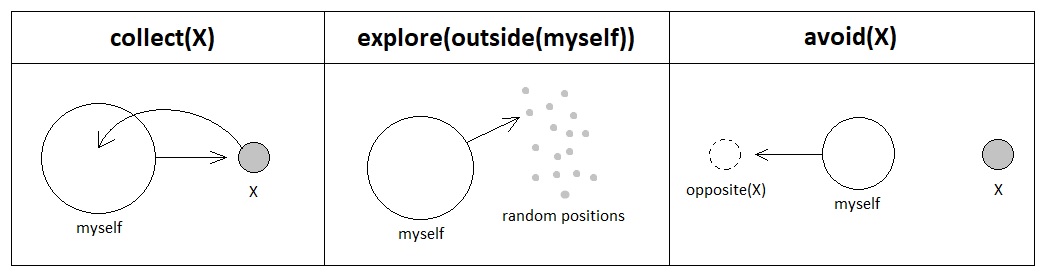
The most optimal way of satisfying the goal "decrease(d+)" with respect to a nearby resource is to not just get closer to it (since the distance "d+" will still be nonzero as long as the protagonist's center of mass does not perfectly coincide with that of the resource), but also to pick it up and put it inside one's own body. Since both the protagonist and the resource are theoretically a pair of mathematical points, putting one of them "inside" the other naturally makes their centers of mass overlap and hence reduces "d+" down to exactly 0. The process of approaching a resource, picking it up, and putting it inside one's body can be denoted as "collect(resource)". This interpretation of "decrease(d+)" also matches the functional implication of a resource because one must ingest it first in order to digest and extract nutrients out of it.
The most optimal way of satisfying the goal "increase(A)" is to conduct one of the two aforementioned methods of expanding one's region of influence - that is, either visit a place which has not been visited for a while (in order to recharge its potential to transmit the organism's chain of causality), or create an offspring who will help expand the region instead. These two procedures can be denoted by "explore(outside(myself))" and "create(offspring)". The function "outside(myself)" indicates the set of all points in space which belongs to the outside of the organism's own body (which, in our case, can be defined as the set of all points in space minus the current position of the organism).
The most optimal way of satisfying the goal "increase(d-)" with respect to a nearby obstacle is to either avoid it (because getting farther away from the obstacle increments "d-") or destroy it (because destroying the obstacle, while it may be significantly harder then simply avoiding it, will instantly change the distance between myself and the obstacle to be greater than or equal to the minimum distance between the earth and the heaven). These two procedures can be written as "avoid(obstacle)" and "destroy(obstacle)", respectively.

So far, one may have acquired an impression that I am now delving into an endless rabbit hole of arbitrary details which are hardly anything more than a mathematically elaborated pile of wishful thoughts. But please bear in mind that there is a definite end to the process which I have been undergoing, and by the time the end exposes itself, it will complete the full picture of how all these functional specifications are supposed to come together and fit nicely into a unified design methodology.
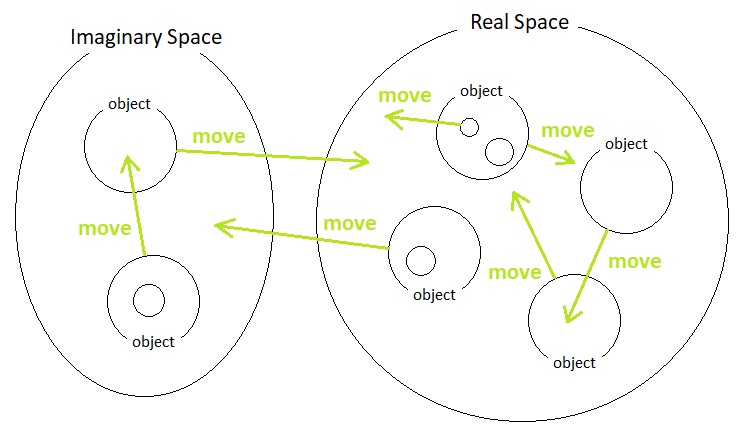
Let's break down the procedures further. We have a bunch of new semantic elements called "collect", "explore", "avoid", "create", and "destroy", which are secondary goals aimed to solve their respective primary goals (i.e. "absorb", "expand", and "secure"). A person who is well-versed in computer science will easily recognize a recursive pattern here and proceed to attempt to break down these elements even further, thereby yielding tertiary goals from secondary goals, quaternary goals from tertiary goals, and so forth. Eventually, what we expect to witness is one gigantic tree of goals (which is often being modeled as a "behavior tree" in a videogame), in which the top of the tree indicates the most abstract goals, whereas the bottom of the tree indicates their most specific constituents (e.g. "Move object X from point P1 to point P2", etc). The question is, what are the most specific (i.e. "atomic") goals we can ever imagine? Once we know this, we will have a clear notion of what are the exact kinds of primitive actions we ought to implement while designing the computational structure of gameplay systems. And my personal belief is that the most basic form of action, which has the capability of achieving any type of goal when combined together in multitude, is "movement" (expressed in terms of the "move(...)" function).
The reasoning behind this lies upon the process of breaking down the goals. What will the protagonist have to do to "collect" an object called X, for example? One answer which makes topological sense is that hardly anything more than a series of simple movements will suffice. The protagonist can first approach X (i.e. Move the protagonist to X), put X into its own body (i.e. Move X to the inside of the protagonist), and that's it. These two actions, which are nothing more than a pair of discrete movements, allow the subject to "collect" X by first approaching it and then integrating it as part of one's internal inventory space.
The case of the "explore" goal is even simpler. Here, the protagonist only needs to move itself to a random position in space which belongs to the outside of its own body. This can be expressed as a single movement.
The "avoid" goal is also a single-movement goal, the only difference being that the destination of the motion is the opposite position of that of the given object X with respect to the protagonist's position.
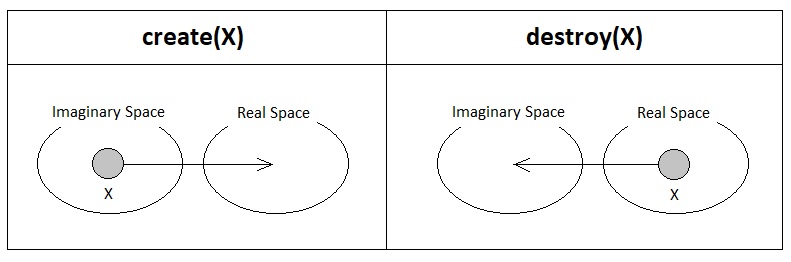
What about "create" and "destroy"? At first, it seems that these two are primitive actions which fundamentally distinguish themselves from the act of movement. If we pretend to believe in afterlife and reincarnation, however, the process of creating and destroying an object can simply be interpreted as the process of transferring its immortal soul from ether to earth or from earth to ether. In more neutral terms, we can say that "creating" an object X is the equivalent of moving X from imaginary space to real space, whereas "destroying" an object X is the equivalent of moving X from real space to imaginary space.
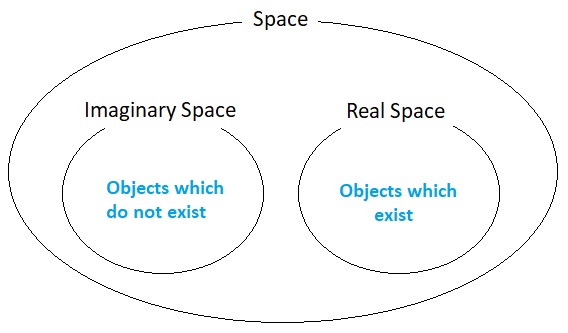
Real space represents the set of all points in space that are currently defined as "existing", whereas imaginary space represents the set of all points in space that are currently defined as "not existing".
The five operations I have described so far (i.e. "Collect", "Explore", "Create", "Avoid", "Destroy") can be written algebraically as well. Notice that the right-side expressions are all made out of "Move" procedures only.

If we substitute the inner procedure calls of the 3 most fundamental goals with their respective right-side expressions, we get the fully expanded sequences of actions as shown below.

The implication of this is pretty neat and minimalistic, despite the seemingly complex list of steps we had to go through algebraically. The fact that life's three most fundamental goals (Absorb, Expand, Secure) can be broken down into mere sequences of movements and nothing else suggests that the entire narrative space of the game can be defined as a purely mechanical system represented by the collective sum of energy particles and their atomic movements.
This allows us to design a game with a methodology that is reminiscent of a scientific experiment in a laboratory. Once we know how the individual atoms behave, we will know how they combine with each other to form molecules. Once we know how these molecules behave, we will know how they will interact with one another to form large-scale molecular structures such as crystals. Eventually, once we know how these structures behave with respect to their circumstances, we will know how to leverage their characteristics for the purpose of manufacturing certain types of materials that are useful for industrial applications, and so on.
The same scientific reasoning can be applied to the study of game design as long as we start by breaking it down to its most atomic constituents and then figuring out how to assemble them one by one for the purpose of creating more and more complex structures. In our case, the "atomic constituents" are simple discrete movements of indivisible objects.
Now, of course, one may as well suspect that the model illustrated so far, which is composed of mathematical points in space and hardly anything else, is way too simplistic to provide the designer with enough room for devising rich gameplay experience. Indeed, the set of alternative player choices listed so far have been quite limited in scope, and they alone will not let anyone create a vast landscape of narratives which is typically expected in today's videogames.
The gameplay dynamics that have been explicitly illustrated so far do not confine themselves in their present state of demonstration, though. They are but an infinitessimally minuscule subset of game design's possibility space which is awaiting us behind the fort of unconscious, and the journey to explore its mysterious ponds and ravines has just begun.
Before seriously plunging into the essential strategies of exploding the spectrum of gameplay choices from a minimal set of emergent building blocks, let me talk about the definition of the word "offspring" which I have mentioned a few times so far. A typical usage of this word is to indicate somebody's biological child. In our context, however, its meaning is a bit more abstract.
The topmost goal of an organism is to secure and expand its region of influence, and the major difficulty which arises when it tries to keep growing its region's size is that the region itself is not a permanent entity; it has a tendency of eroding over time, as well as being overtaken by other organisms' regions. So it is not wise for the organism to merely keep recovering the weakest portions of its region by moving back and forth as frequently as possible, for it is a common sense that it must have its own speed limit as well as the necessity to constantly refuel itself with external sources of energy (e.g. resources), which are not always available instantaneously. Such a monotonic strategy is bound to introduce a hard limit to the maximum size to which the region can grow. A better method to guarantee the unbounded growth of the region would be to produce "offsprings" which will be emitting their own forces of influence around their positions in addition to those of the parent, thereby splitting the amount of responsibility it takes to maintain the current area of the region.
The offspring mentioned here do not have to be one's biological descendants; they may as well be one's properties such as livestock, pets, real estate, goods, and other objects which can be owned by the organism, or may even be abstract ones such as the organism's intellectual properties (e.g. patents), financial assets, reputation, credit, personal relationships, information, and others which can be deemed to help expand the region of influence.
These offsprings, abstract or non-abstract, collectively form the holistic definition of "myself" from the organism's point of view. When I own a car, it becomes part of my extended self despite being a vastly separate object from a purely mechanistic view. The reason why I can say this is that, since I own it, anyone who damages the car will have to pay me for it (at least from a legal perspective). This establishes a direct causal connection between the influence of my own existence and the influence of the car's own existence. If the car's area of occupation gets intruded, the intruder will be affected by the influence of mine (as a citizen protected by property laws) by having to pay for the act of offense. Therefore, it could be concluded that the car's area of occupation is a subset of my region of influence, and hence the car itself can be expressed as a point mass which constantly replicates my forces of influence around its current position. This is what an "offspring" is in our abstract context - an alternative point in space which extends the owner's influence beyond the physical reach of one's own body.
And there is a great deal of diversity in gameplay we can extract from the presence of offsprings. Suppose, for example, that there is an offspring called X.
Previously, we only had 3 variables which were labeled as (d+, A, d-). Now with the presence of an offspring, we have 6 variables instead: (d1+, A1, d1-, d2+, A2, d2-). "d1+", "A1", and "d1-" are the same ones as introduced before; they are the protagonist's distance from a resource, the area of the protagonist's region of influence, and the protagonist's distance from an obstacle, respectively. "d2+", "A2", and "d2-", on the other hand, are quantities of the same exact meaning except that they are measured with respect to the offspring X instead of the protagonist.
(d1+, A1, d1-) represent the metrics for tracking the performance of the protagonist's own body, while (d2+, A2, d2-) represent the metrics for tracking the performance of the offspring's body. And since these variables come in pairs such as "d1+,d2+", "A1,A2", and "d1-,d2-" (which can be expressed as 2D vectors) instead of isolated scalar quantities, each of the lifeform's three most fundamental goals can now be represented as a pair of alternative goals instead of just one (one for changing the left side of the pair, the other one for changing the right side of the pair).
The sub-goals "decrease(d2+)", "increase(A2)", and "increase(d2-)" can be expanded as shown in the picture below. The actions required to fulfill these goals are quite different from ones which associate themselves only with the parent and not its offspring. In this new circumstance we are facing here, the subject of these new goals is the offspring. However, it is still the parent who is carrying out these goals, which means that the way to accomplish them (from the parent's perspective) is to "help" its offspring to absorb, expand, and secure instead of directly pursuing them on its own because the parent is not a ghost that can just possess the offspring's body and have direct control over it.

And again, all of the subsidiary tasks involved in following the goals above can be fully expanded into sequences of discrete movements, which can be translated directly into machine instructions in almost any computing device.

Aside from alternative choices which arise from the presence of an offspring, there may also be alternative choices which arise from the organism's ability to bring a new offspring into existence. For example, one may destroy an obstacle by creating an offspring called "bullet", moving it to the inside of the obstacle's body (by means of "shooting"), and then letting the bullet carry out its own "secure(...)" goal by destroying the obstacle. The converse is also feasible. One may as well destroy (explode) one of its offsprings called "bomb" for the purpose of destroying its nearby obstacles as a side effect. The act of destroying one's offspring disobeys the organism's "expand" goal (since the annihilation of an offspring shrinks one's region of influence), yet it also allows the organism to obey its "secure" goal by getting rid of obstacles, which can be considered a decent choice to make if the latter brings more benefit to the organism than the former. Such an exchange between two competing goals (i.e. sacrifice of one goal for the sake of another) is an intelligent decision which the organism can be expected to display if it is a well-designed AI agent, or if it is a player-controlled character.
Such methods of endlessly spreading one's assortment of imagination, however, may not be adequate for our purpose of penetrating into the essence of emergence in gameplay. In the next volume, I will explain how the dynamic elements which have been mentioned so far will be able to fit together in the overall methodology of game design.
(Will be continued in Volume 3)
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service