
Author: Youngjin Kang Date: 2023.05
(Continued from Volume 14)
In the previous volume, I introduced the idea of decomposing the whole game into a cascade of multiple subroutines called "mini-games" for the sake of simplifying the design process. As I hinted during the first half of volume 1, a game can be represented as a sequence of sub-goals which ultimately contribute to the fulfillment of the player's ultimate goals as a biological entity: "Absorb", "Expand", and "Secure". Since the full chain of such sub-goals is way too convoluted to be depicted as a single mathematical construct, it should be deemed wise to break it down into mini-games each of which is designed to direct the player's attention to only one of such sub-goals instead of all of them at once.
And since the behavioral nature of any organism (at least within a particular theoretical context which I have been assuming so far) can be modeled in terms of the changes in its distances (i.e. pathfinding costs) from 3 distinct types of atoms which are denoted by "Resources", "Influences", and "Obstacles", it should be also wise to suppose that each mini-game guides the player's behavior based upon the presence of its own temporarily defined set of resources, influences, and obstacles.
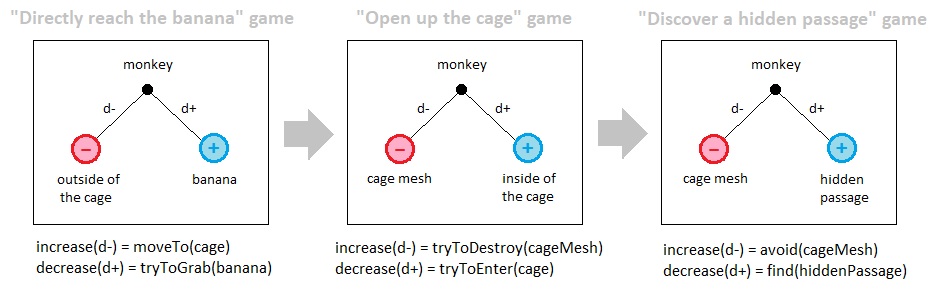
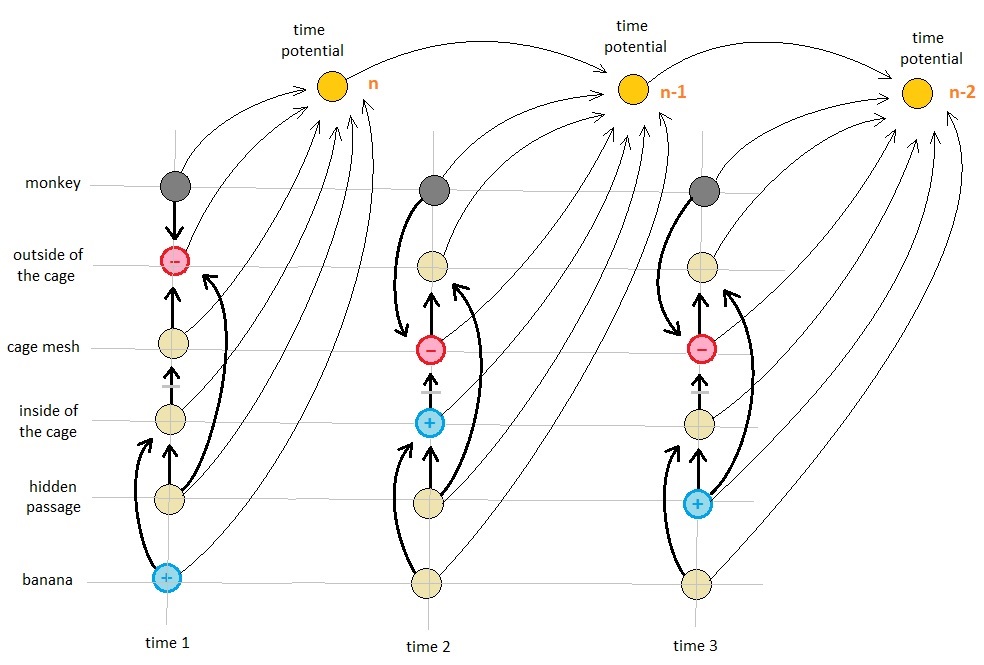
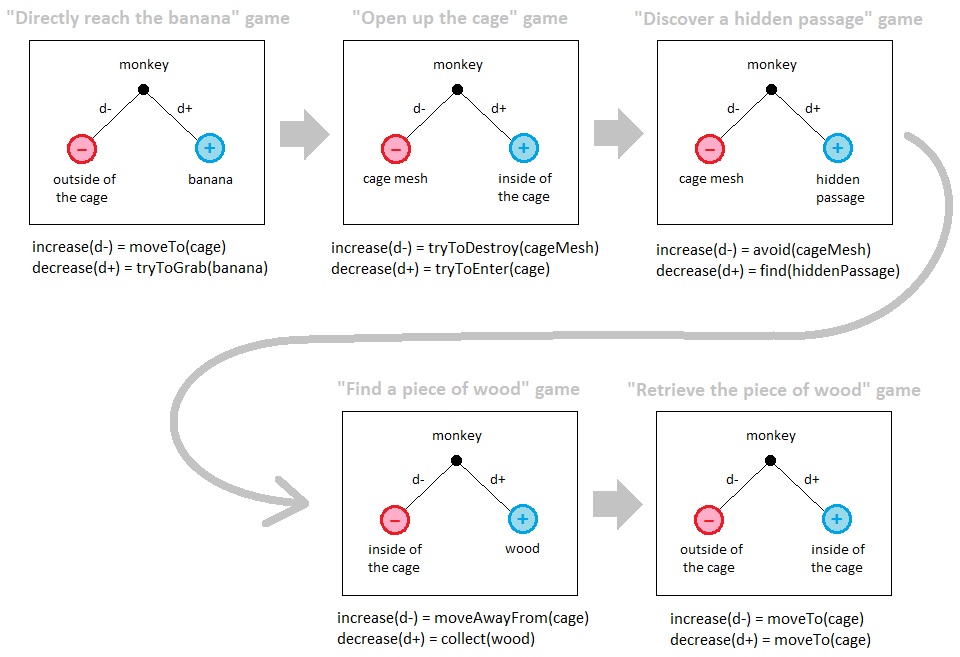
Let us go back to the monkey example which was introduced in the previous volume. Here, each mini-game can be considered a separate universe - a universe which possesses its own set of resources and obstacles for the monkey to interact with. In the first mini-game, the outside of the cage is the monkey's obstacle because approaching the center of the cage (i.e. the place where the banana is located) is basically the same thing as running away from any location which exists outside of the cage. Meanwhile, the banana is the monkey's resource within this mini-game because the monkey is expected to simply stretch its arm towards the banana during its very first attempt to acquire it. In the second mini-game, the cage's mesh is the monkey's obstacle and its inside is the monkey's resource because such a configuration propels the monkey to try to open up the cage by trying to destroy the cage's mesh (in order to move it to the heaven (i.e. imaginary space)) while also trying to sneak into the cage as soon as part of it gets destroyed. In the third mini-game, the cage's mesh is still the monkey's obstacle but now a hidden passage which leads to the inside of the cage (if it exists) is identified as the resource instead.
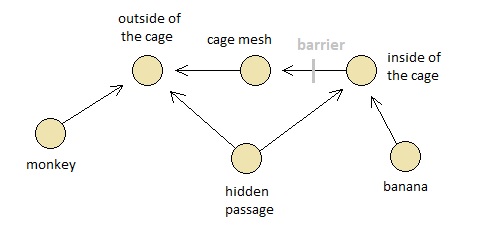
These three mini-games all happen in the same place (i.e. game console), though. Therefore, it is sensible for us to think about the overall time-invariant representation of the gameplay space with which the monkey is engaged, which is basically the union of all spatial entities and their network of mutual bindings found in all of the aforementioned mini-games. Inside such a holistic view, everything is an atom; the monkey is an atom, the outside of the cage is an atom, the inside of the cage is an atom, and so on.
The three mini-games are nothing more than different interpretations of the same overall picture, which may be referred to as separate parallel universes whose characteristics differ based upon the observer's motivational state. In the first mini-game, the monkey tries to directly reach the banana which is located somewhere that is not part of the outside of the cage. Thus in this particular scenario, the monkey defines the outside of the cage as an obstacle (which is must avoid) and the banana as a resource (which it must follow). The rest of the two mini-games follow the same kind of logic.
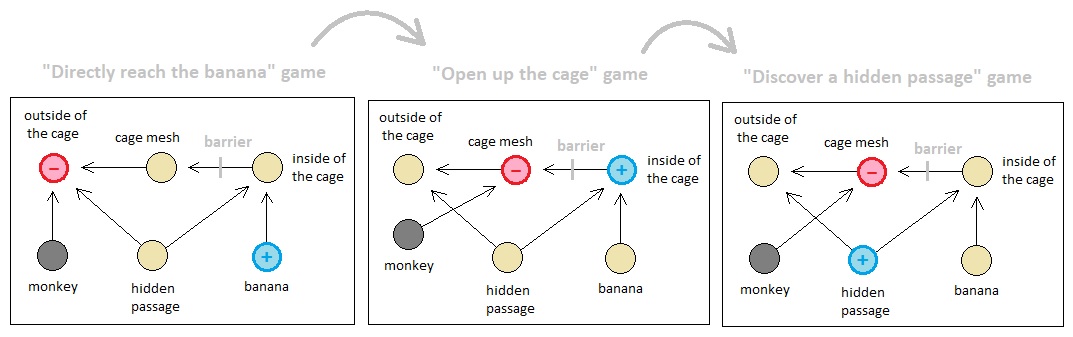
Once the three distinct parallel universes are superimposed into a single unified picture, we see the full landscape of the game's narrative in the form of multi-stage resources/obstacles, where each stage is denoted by an index such as 1, 2, or 3 (referring to the 1st, 2nd, and 3rd mini-games, respectively).
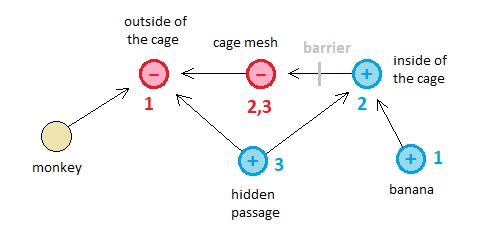
And if we expand this model into distinct time intervals each of which represents the duration during which the monkey gets engaged in each mini-game, we will obtain the landscape of the monkey's gameplay in the form of a space-time continuum. In this model, the agent which plays the first mini-game is the copy of the monkey-atom which belongs to time 1, the agent which plays the second mini-game is the copy of the monkey-atom which belongs to time 2, and the agent which plays the third mini-game is the copy of the monkey-atom which belongs to time 3.
The ultimate purpose of the game, of course, is not just to entertain the monkey by letting it find its way to the banana without necessarily benefiting the owner of the game console. The machine will eventually have to encourage the monkey to insert a piece of wood into its deposit box (This is a monkey version of "Pay to Win"), and such a peculiar kind of motivation should not be expected from any of the 1st, 2nd, and 3rd mini-games which were illustrated above.
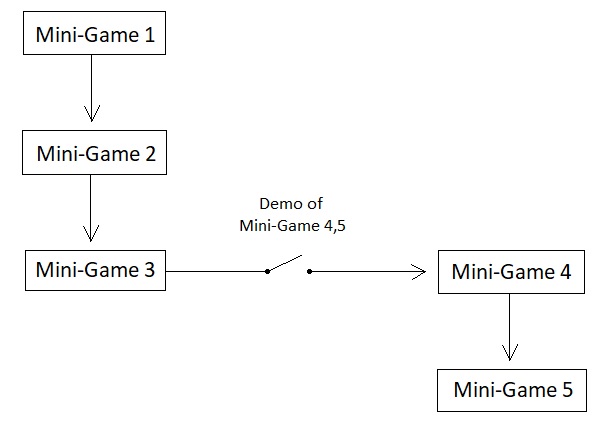
The solution to this problem is straightforward; we just have to add additional mini-games to the monkey's expected course of gameplay. Let us assume that there is the 4th mini-game which is designed to inform the monkey that inserting a piece of wood into the machine will help it obtain the banana. How will this 4th mini-game have to be designed to serve such a purpose?
First of all, we do not know the language of monkeys in a sufficiently accurate manner and therefore cannot afford to come up with an NPC who will appear before the monkey and say the sentence: "Bring a piece of wood and I will give you a banana!" in monkey-speak. So we must communicate with the monkey based upon a universal language called "demonstration". All we have to do is periodically display a live demo of the feedback loop between a wooden piece and a banana in front of the monkey, either by means of a video footage on a screen or by means of a mechanical automaton which involves a robotic monkey and a fake banana. The demo can simply show a virtual monkey dropping a piece of wood into the machine and getting a banana as a reward, dropping another piece and getting another banana, dropping yet another piece and getting yet another banana, and so on (in a cyclic manner, repeating the same sequence of events indefinitely). This will make the monkey realize that, since it has become quite apparent (after playing the 1st, 2nd, and 3rd mini-games) that there is no way to directly reach the banana, or to open up the cage, or to find a hidden passage, the only remaining solution is to watch the live demo and mimic what is happening inside of it.
Once the monkey copies the behavior shown by the demonstration footage, fetches a nearby piece of wood, and puts it into the game console's deposit box, it will immediately verify that the scenario showcased by the demo is indeed an accurate reflection of reality by seeing an actual banana dropping in front of it as a reward. After this initial confirmation, we can pretty much assure that the monkey will bring more and more pieces of wood and drop them into the box for the purpose of earning more and more bananas. As long as the amount of effort it takes to find a new piece of wood and bring it back to the machine is smaller than the amount of effort it takes to find a natural source of food (e.g. a naturally grown banana on a banana tree), the monkey will be engaged in this artificial feedback loop whenever it gets hungry.
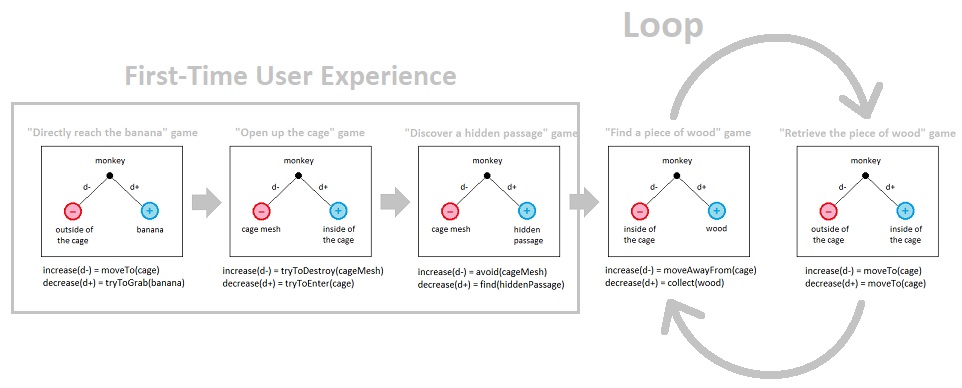
On a schematic level, this whole feedback loop can be broken down into two mini-games - namely, the 4th and the 5th. The 4th mini-game begins as soon as the monkey watches the demo and learns about the quest it is required to carry out in order to receive the reward it desires (i.e. banana). In this mini-game, the monkey interprets any piece of wood as a resource because it is what it needs to collect in order to unlock the "reward" side of the feedback loop. The inside of the cage, on the other hand, is interpreted as the monkey's obstacle because visiting locations that are part of the cage itself won't help the monkey discover a piece of wood.
Once the monkey successfully gets ahold of a piece of wood, the 5th mini-game begins. In this mini-game, the inside of the cage is interpreted as a resource because the monkey is supposed to bring the piece of wood back to the cage in order to complete the mission, and the outside of the cage is interpreted as an obstacle because one's desire to approach the cage is the same thing as one's desire to run away from any location which belongs to the outside of the cage.
The thing is, the monkey won't just stop right after it receives its first reward. It will continue playing the game by repeating the 4th mini-game and 5th mini-game multiple times (i.e. finding and retrieving more and more pieces of wood) in order to receive the same reward over and over again, until its stomach becomes full. Unless it somehow forgets its initial experience with the machine, however, it will never repeat the first three mini-games because those have already been proven to be ineffective. So the first three can be considered the monkey's FTUE (First Time User Experience), as opposed to its main gameplay loop which consists of the 4th and 5th mini-games.
But of course, this constantly rewarding gameplay won't last that long because each monkey can manage to eat only a fairly small number of bananas at a time. One may consider reducing the size of each reward down to only a small portion of a banana in order to alleviate this problem, yet such a kind of reduction risks potential loss of interest due to its decreased level of cost-effectiveness; that is, the monkey may simply think, "Why bother searching for a piece of wood in the first place, if all I am promised to get is just a tiny subsection of a banana? I will rather just directly search for a banana tree instead, where I can expect to find whole bananas and even bundles of them!"
A better solution to this is to turn the game console into a slot machine. Instead of handing over the exact same piece of reward to the monkey every time it accomplishes a mission, this machine would sometimes hand over a relatively large treat, sometimes a relatively small treat, or sometimes nothing at all (depending on the result of a dice roll). This gambling mechanic will motivate the monkey to be way more intensely engaged in its wood-fetching activity than it would've been if its earnings were highly predictable in nature, for such a configuration introduces an uplifting sense of fascination which springs from one's expectation of a "surprise reward" - a jovial sort of hope which makes the monkey dream of winning a huge fortune during its next trial, thereby driving it to play the game over and over gain just for the sheer anticipation that its own fantasy will make an unprecedented visit and knock the door of reality at some point in time.
And we can proceed to add more and more design elements to the game as needed, which will enrich the monkey's gameplay experience further and further until we are assured that the game console is sufficiently effective in terms of generating revenue out of monkeys in the forest. We may consider employing intransitive mechanics, rubberbanding, exponential/logarithmic progression curves, and myriads of other strategies for maximizing the profit. However, full exposition of such technical details is not what these articles are intended for.
To recap, I would say that the initial motivation behind the search for "universal laws of game design" was the desire to introduce a purely mathematical model in which all sorts of seemingly vague gameplay concepts become endowed with the privilege of merging themselves into a set of strictly quantitative definitions, rather than an endless continuum of case-by-case examples and generic marketing phrases.
And throughout all volumes of this series of articles, it has always been of the foremost priority to ensure that such a pure structure of reasoning be invariably preceded by our common understanding of the physical reality which surrounds us, which comprises space, matter energy, information, and other shared conceptual elements which, when combined, constitute the dynamics of our universe.
A fictional gameplay universe is made up of atoms, each of which may represent a spatial location, an energy particle (which could belong to not just one of physical kinds, but also one of psychological kinds such as emotions), a part of a mechanical body, a volitional element, or any other physical/metaphysical entity which can be considered indivisible. From an arrangement of atoms and their relations, various mechanics and narratives emerge both of which reinforce one another in a cyclic manner (Mechanics give birth to new narratives, and narratives give birth to new mechanics). And since it is possible to mathematically define atoms and their relations, it must also be possible (under the principle of additivity) to mathematically define their ensuing mechanics, narratives, and their suggestion of gameplay as a whole.
It is likely to be argued, though, that the theoretical model which has been devised so far is way too structurally abstract to be comprehended and/or utilized by most people, except ones who are quite familiar with discrete mathematics. And this is a perfectly valid argument, especially when we notice that one of the primary goals of the universal laws of game design is to make sure that they are "universal" in the sense that anyone who possesses a decent level of academic literacy must be able to grasp their nature regardless of one's own area of expertise.
However, it should also be noted that the symbols and numerous other notations I have used so far to explain these universal laws are not an absolute set of grammatical rules which we all most follow with utmost precision. After all, it is the underlying body of concepts that is of our interest, rather the specific syntax we choose to express them. In a practical scenario in which we are to design a game, we probably do not want to draw out every energy particle, every signal particle which may be transmitted from one place to another, every potential which may or may not let an energy particle come in or move out, every minuscule body part of an organism, or every single point in space as an atom and its collection of bindings. So for efficiency and ease of understanding, we may consider introducing notational conventions (i.e. syntactic sugar) to the way in which we represent our model.
If we assume that our gameplay space comprises a two-dimensional grid of voxels, for example, it is more intuitively satisfying for us to denote each voxel (i.e. spatial location) by a square area instead of an atom. Also, it is more intuitively satisfying for us to denote each energy potential by a small numerical label attached to the corner of its containing voxel, which tells the location's energy-type and energy-level.
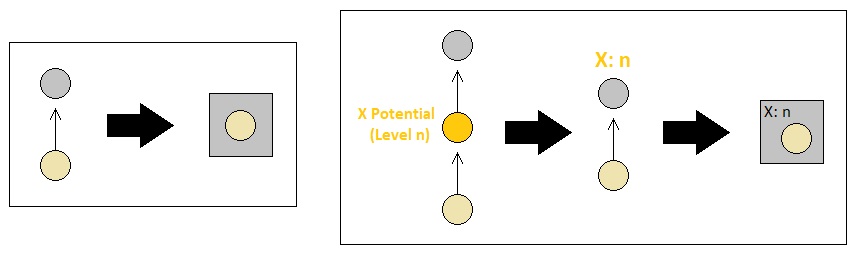
Also, while it has conceptually been supposed that a connected pair of component atoms in a compound object basically have their medium of communication be made of a "connector" atom which works as an intermediary (like a telephone wire) for the sake of functional modularity, we find that such a representation is way too notationally verbose. Therefore it is often desirable in practical circumstances to simplify the expression of such a concept down to a single line segment rather than a whole separate atom to which both of the ends are bound.
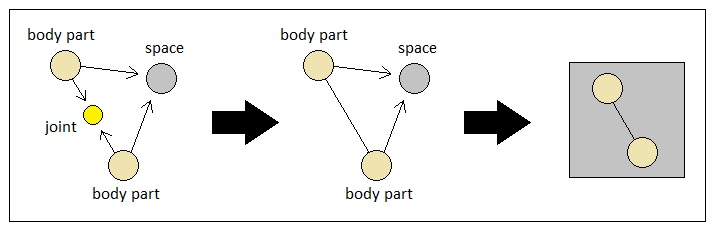
When an object is made up of multiple atoms, we can imagine that some of them may belong to the same voxel while others may not. Fully specifying such a state of locational diversity purely in terms of atoms and their bindings tends to make things appear too complicated. If we use the notational conventioned stated above, however, the resulting graphical representation becomes so clear that even people who do not understand high school math can see what is going on.
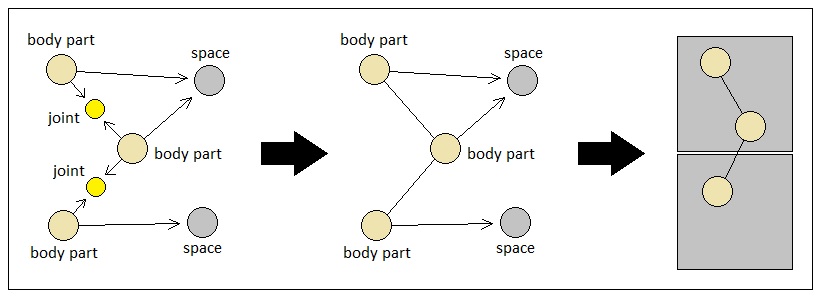
From a holistic viewpoint, we can easily see that the aforementioned set of simplifications help us design our gameplay world in a crystal clear manner. In this discrete universe which is reminiscent of a tabletop game, every point in space is a voxel whose coordinates are just the row and column of the grid. Every object is made up of one or more atoms, each of which occupies one voxel at a time as its current position. And both a voxel and an object-atom can have a list of numbers attached to itself, where each number refers to the energy-level of a potential through which energy can be transmitted.
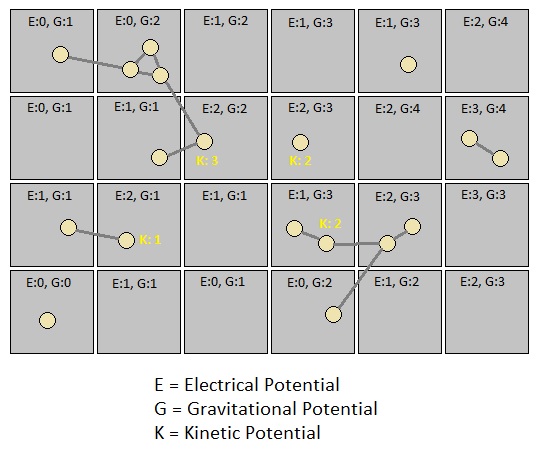
The space (i.e. grid) is filled with various types of energy potentials and their respective levels, and differences (aka "gradients") between levels of adjacent potentials essentially constitute a "force field" which can be depicted as a distribution of vectors in space. Atoms are naturally disposed to follow these force vectors, which means that we can manipulate the way in which atoms move by simply warping the shape of their field (That is, by changing the energy levels of potentials). And the process of motivation, besides its initial interpretation as an act of temporarily adding a "motive molecule" to the arrangement of atoms, may alternatively be represented as an act of temporarily incrementing/decrementing the levels of a specific group of potentials.
As a whole, this conceptual framework is so generic yet endowed with a sense of mathematical precision, that it is not so hard to imagine the possibility of all sorts of intriguing applications which can be brewed out of it. A wide spectrum of sandbox elements (such as doors, switches, traps, storages, and many others), for instance, can be implemented by first arranging multiple pathways through which certain types of energy exchange can happen, and then letting specific types of events turn on/off some of these pathways in a selective manner (e.g. A key unlocking a door, a foot triggering a signal by stepping on a pressure plate, etc).
This concludes the overview of concepts and their methods of realization in our search for "universal laws of game design".
Since a game is a fairly complex universe in which countless mechanics and narratives are intertwined with one another, it may be claimed that we cannot take account of all of its intricate details and their ensuing varieties. And it is a perfectly valid argument for sure. However, just because something is complex does not mean that we should remain clueless about it and simply confine ourselves to mere trial-and-error methodology. Just as psychology, sociology, political science, economics, and many other academic subjects endeavor to explain the nature of complex systems based upon generalized models, one should regard a similar attempt in the field of game design not as a sign of "overthinking", but as a genuine intent to figure out a reusable set of building blocks out of which games can be assembled.
(End of "Universal Laws of Game Design")
Previous Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service