
Author: Youngjin Kang Date: 2023.04
(Continued from Volume 12)
The possibility of interspecies gaming becomes more and more of a serious business as we consider our upcoming future. As I explained in the previous volume, the necessity of endowing our primary industries (e.g. food and energy production) with the power of autonomy will be more of everyone's interest than ever due to the dwindling degree of reliability in our current mode of global free trade. As the overall degree of mobility in our system of resources decrements, we will be forced to develop some kind of self-sufficiency in our utmost daily needs such as food and petroleum.
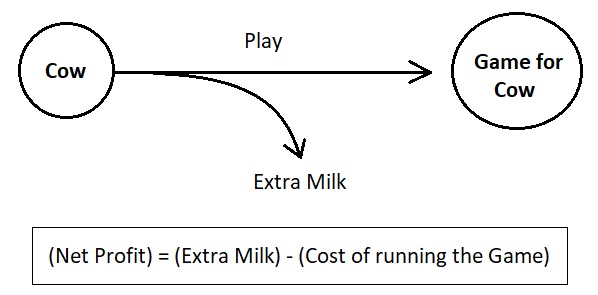
And here is a solution. If we design games which can be played by our planet's ecosystem (rather than by human consumers), we will enable ourselves to dig out all sorts of natural resources from our mother nature in an almost fully automatized manner. In a way, thus, we will be entitled to fancy that a "universal game design framework" which is robust enough to serve such purposes must be a sustainable passive-income generator which will extract revenue from the environment by means of dynamically interacting with its ecological participants (i.e. animals, plants, microbes, etc). Every living thing in any biological habitat, such as a forest, a river, a cowshed, or a fish tank, is a potential player which might be able to "pay to win" by utilizing its biological activities in ways which are beneficial to human beings. If a cow plays a game and gets induced to produce extra milk as a result of playing it, for example, we will definitely be able to declare that such a game is a tool for generating revenue in the dairy industry.
In order to be able to design games which are capable of being played by a variety of non-human species, however, we must first come up with "universal laws of game design" which are applicable not only to human players, but also to species whose biological input/output patterns differ greatly from those of humans. And in order to sort them out in forms which can be specified and implemented in practical scenarios without too much hassle, we must establish their logical foundation upon the principle of "mathematical minimalism" and "quantitative expansion" (explained in volume 4). "Mathematical minimalism" allows us to represent abstract concepts without introducing too much complexity, while "quantitative expansion" allows us to keep adding more and more details to our system without introducing additional rules.
While this may be theoretically sound, it is also true that most game developers are likely to be confounded by the notion of building gameplay systems out of such a generic framework which does not specify any "fun" part of the game in particular. Yet, the apparent absence of such a superficial emotion in our conception of the theory makes perfect sense because our shared definition of the word "fun" is more or less confined to the sense of entertainment being felt by human beings, rather than a wide range of interests being shared by a wide spectrum of biological niches which altogether constitute our ecosystem.
Still, it is nevertheless crucial to find a good reason to assure that it is possible to derive a viable set of implementation strategies which are in sync with the aforementioned laws of game design. Once it is proved, we will be able to tell that the idea of constructing universally applicable games out of such laws is not just an assortment of academic imaginations, but more of a body of mutually consistent theories which contribute to the development of a practical business solution.
Let us look back at the overall formulation of the theory which has taken place so far. On the most materialistically fundamental level, we have atoms and their bindings which conceptually represent regions in space and their input/output relations respectively. Each region may denote a spatial location, a unit of energy, an energy potential, an object, a component of an object, or any other entity which is discrete in nature.
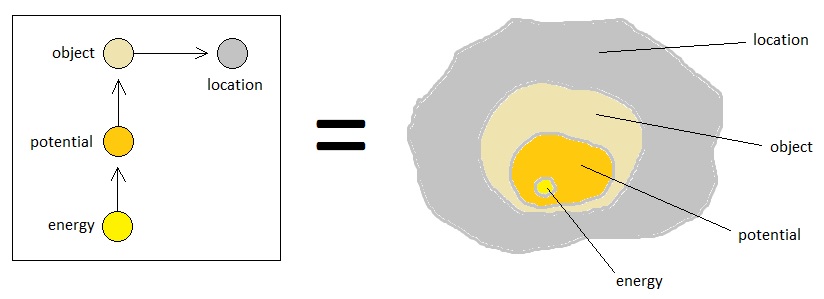
When we think about the nature of a gameplay world, we often conceptualize it in terms of "things" which occupy portions of its spatial volume. Such "things" can be interpreted as atoms, since the idea of modelling a universe as a collective sum of its smallest indivisible units (aka "atoms") helps us design its nature in a strictly quantitative (therefore logically traceable) way.
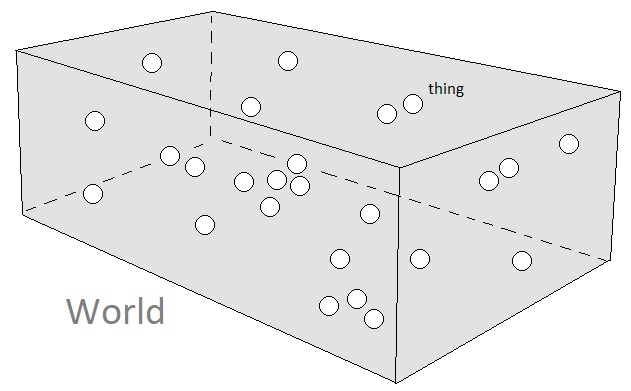
Representing a universe solely based upon its material composition, however, is inadequate for game design purposes because it only shows half of the full picture. A game consists of both mechanics and narratives, which continually augment and rectify each other in a cyclic manner. While material bodies and their respective physical motions do have the capacity to describe the game's mechanics, they do not fully explain (at least in the practical sense) the dynamics of living things and their emotional behaviors. Therefore, aside from a collection of atoms which represent the physical entities of the world, we need yet another collection of atoms which represent the narratives of those entities. What is perhaps the most intuitive form of such a collection is a tree of goals, in which each component node is an atom denoting a goal to pursue.
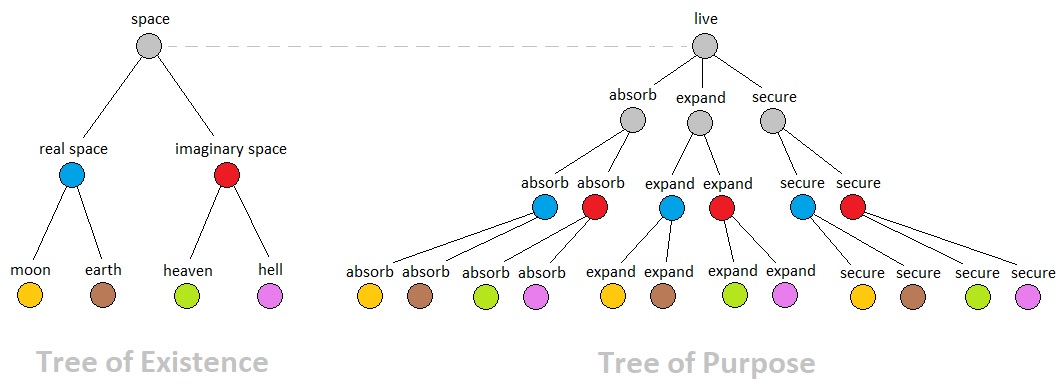
From a holistic viewpoint, what we implicitly observe is a pair of trees which can respectively be labelled as "Tree of Existence" and "Tree of Purpose". The former is the universe's overall hierarchy of mechanical beings, whereas the latter is the collective hierarchy of their goals. The Tree of Existence continually modifies the structure of the Tree of Purpose, while the Tree of Purpose continually modifies the structure of the Tree of Existence (by adding and subtracting "motive molecules", as demonstrated in volume 10). This gives birth to a cycle of mutual reinforcement between the game's mechanics and their respective narratives. Anyone who has control over both of these two trees must have full control over the universe.
One might question this way of modelling by saying, "So, why represent the whole game as a pair of trees which are made up of individual atoms and their hierarchical associations? Wouldn't it be a much better idea to simply represent the game world as one continuous Euclidean space, in which all sorts of geometric shapes can reside and play their own roles as gameplay agents such as the player, NPCs, props, obstacles, traps, and so forth? Why bother introducing obscure topological concepts to the scene, if we can leverage the knowledge of our natural geometry as means of triggering a variety of in-game events?"
This question makes perfect sense to a certain extent, except that such a Euclidean model begins to reveal its own severe limitations as soon as we go deeper into the subject of gameplay dynamics and their ensuing suggestion of complexity.
When we represent our in-game objects as geometric figures instead of a topological network of nodes, what we are immediately bound to realize is the necessity to design our game mechanics based upon fairly complicated geometric calculations such as those which pertain to global/local coordinate systems, vector math, spatial hashing, collision detection, raycast, and many other mathematical constructs which are not clearly understood by most game development professionals whose areas of expertise are outside of the domain of engineering. Unless it is one's intention to exclude anyone who is not well-versed in mathematics from being part of the game design process, it is necessary to start the conceptual foundation of the gameplay universe from a model that is much more approachable from a layman's perspective (That is, discrete atoms and their bindings).
Aside from the ease of comprehension, there are two other reasons why our discrete model is superior to geometric representations. One is that it is much more convenient to express complex objects as an assembly of discrete functional components than to express it as a continuous volume in space (for it is not so difficult to imagine that space itself does not intrinsically possess rooms for functional endowment), and the other one is that it is way easier to implement discrete components and their relations in our digital computers than things which are spatially continuous (aka "analog") in nature.
In order to demonstrate the ease of implementation, let us first suppose that we are planning to develop a computer game based upon the "universal laws of game design" introduced so far, using a conventional programming language such as C/C++ along with a conventional development framework such as OpenGL. There are other equally viable means of implementation, but being able to create a game inside our modern general-computing framework seems to be a decent starting ground for the purpose of proving that these "universal laws" really are universal in the sense that they can be applied to games which are playable in most commercial electronic devices (such as PCs, tablets, phones, game consoles, etc).
(1) Computer-Based Implementation
If the basis of our game design began with the conception of Euclidean space, prototyping a game would have been a massive pain due to the fact that it would require us to equip the project with math, graphics, and physics libraries just to demonstrate the core dynamics of the design. Fortunately, we do not have to deal with such technical details when we represent every in-game component as a discrete entity called "atom", since it can simply be implemented as a chunk of data (i.e. struct), stored as an element of an array. Its bindings are nothing more than pointers which point to other atoms in the array.
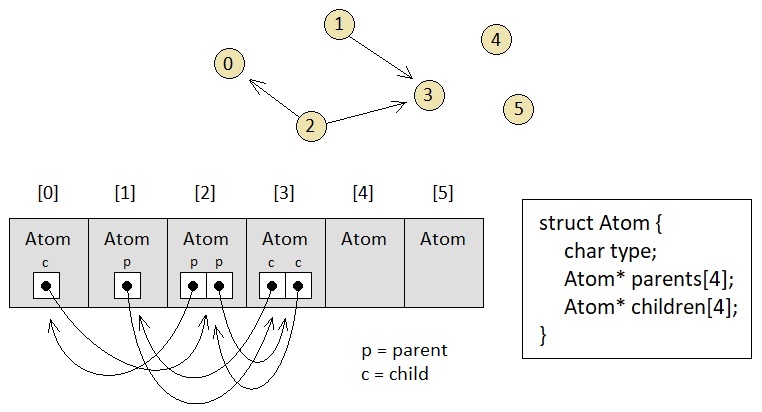
Components of a physical object, positions in space, signals, signal receptors, energy particles, potentials, and myriads of other indivisible spatial entities can all be described as "atoms" from a purely computational standpoint, and thus they can all be represented as instances of the atom-struct inside this single array.
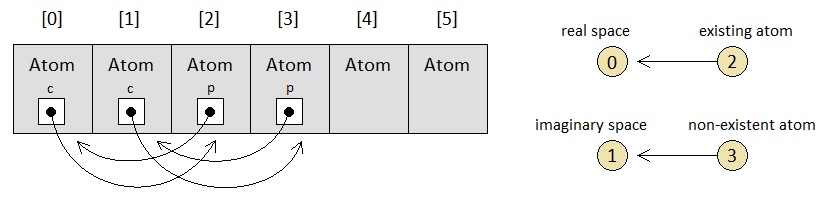
In order to distinguish atoms which "exist" from those which "do not exist", all we have to do is mark the first two elements of the array as "real space" and "imaginary space", respectively, and then make all "existing atoms" point to the real space and all "non-existing atoms" point to the imaginary space. This way, the programmer won't even have to create separate arrays or come up with a clever memory allocation scheme to be able to endow them with separate existential characteristics. Pointer values (i.e. bindings) will automatically render such distinctions.
Goals, too, can be represented as atoms because they are discrete entities with topological bindings. This means that they are not even the slightest bit different from spatial (physical) atoms in the sense that they are elements in the array of atom-structs. Relationships between gameplay agents and their respective goals can simply be indicated by their mutual bindings (i.e. pointers).
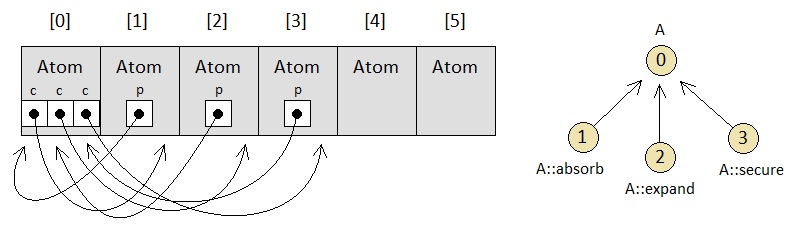
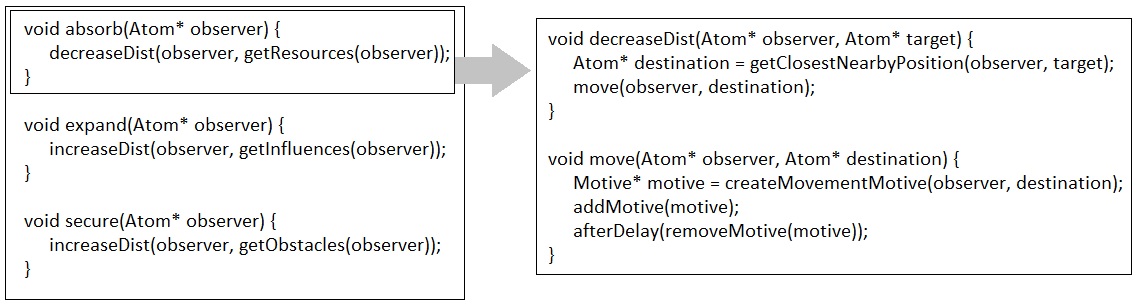
Creation and fulfillment of goals, as well as their subsequent modification of the physical arrangement of things in the material universe, can be implemented as functions which get executed as the program traverses the goal tree. In a way, therefore, the entire goal tree may as well be imagined as the hierarchy of all function calls within the game.
One may object to the notion of designing the whole game based upon atoms and their interconnections, perhaps by saying that our in-game objects are complex beings which possess a wide range of graphically and physically rich components rather than mathematical points in space, such as meshes, materials, hitboxes, joints, bones, animations, and so on. However, we ought to behold that the atom-based model is meant to be the underlying functional skeleton of the game rather than the result of its full implementation. The final product, for sure, cannot be constructed solely out of atoms and their relations. Yet, the idea is that once we have a rigid gameplay framework which can be expressed in terms of these abstract elements (the main benefit of such a framework being that its dynamic nature can be easily understood by all types of game development professionals such as designers, artists, musicians, engineers, QAs, and producers), we can simply proceed to finish the rest of the project by adding separable layers of complexity on top of them.
For example, as long as we suppose that a compound object is a graph made up of atoms and their bindings, it is not difficult to fancy that each of its constituent atoms is an individual body part of a creature, equipped with its own transform, mesh, material, hitbox, physical joint (such as a hinge), and other typical gameplay-related components. These all exist in addition to the underlying atomic representation of the object, which means that all the complexities which arise from the problem of handling various assets and other implementation details can easily be separated out from the core structure of the gameplay. This is the art of modularity.
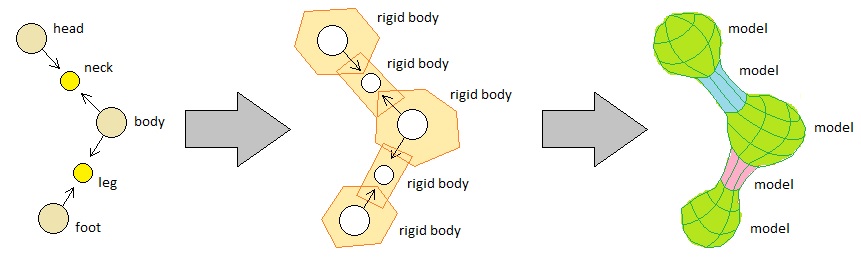
(2) Custom Hardware Implementation
For utmost optimization, one may even proceed to develop games by coming up with one's own custom hardware instead of relying on the computational framework of a general-purpose computing device such as a PC. In such a scenario, too, our atom-based gameplay system turns out to be highly compatible both in terms of design and implementation.
Let us imagine that every one of the atoms in our gameplay universe is a circuit component whose bindings are represented as wires. Since atoms change their bindings as the game progresses, such wires will have to be able to rearrange their endpoints every time the game's electronic clock ticks itself. This means that, on the semiconductor level, it is possible to implement the whole gameplay system by manufacturing an integrated circuit which consists of two layers - the lower one being the two-dimensional array of atoms, and the upper one being the two-dimensional array of wires and their signal routers. By reconfiguring the way in which the routers join their wires with each other, one can reconfigure the way in which the atoms are bound to one another. Creation and execution of goals will be nothing more than mere atom-to-atom interactions which happen via modifications in their respective wire connections, all taking place in parallel and thus allowing the game to run blazingly fast.
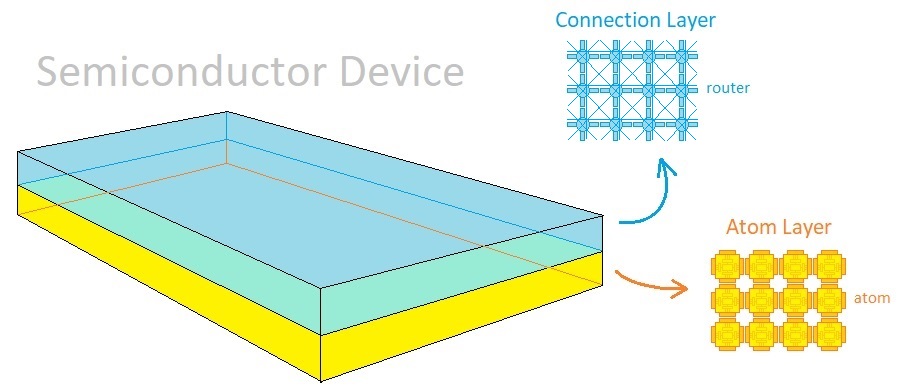
(3) Chemical Implementation
Our atom-based model is even more compatible with a chemical computing system, although such a system has not reached a sufficiently high level of popularity yet. Due to the obvious analogy between our hypothetical "atoms" as the individual building blocks of our game design and the real atoms of our actual physical surroundings, it is not hard to imagine that one has the right to claim the feasibility of building a chemical computer which leverages the science of real molecular interactions as means of simulating the atom-based gameplay model.
As long as we assume that the game world consists of a fabric of space which is permitted to warp its own shape at any time, it will be quite possible to say that every gas molecule which fills up the chemical computer's airtight chamber is a set of "spatial atoms" which represent positions in space (If one wants a strictly 2D Euclidean gameplay space of a fixed shape and size instead, there will need to be a well-polished crystal plane, in which case each atom constituting the surface of its crystalline structure will be interpreted as a spatial atom).
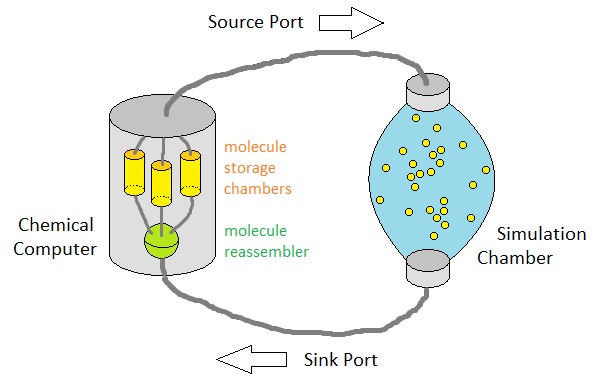
In this chemistry-driven simulation space, each in-game agent is nothing more than a molecular compound which dynamically interacts with other molecular compounds, under the influence of "motive molecules" which are injected into the chamber for the purpose of catalysis. That is, injection of motive molecules can be interpreted as a process of putting some kind of "holistic motives" (i.e. cosmic purpose) to the game's overall landscape of narratives, whereas the subsequent injection of another set of molecules which dissolve those motive molecules (thereby disabling their roles as motivational catalysts) can be interpreted as a process of demotivation which cancels out the state of volitional arousal. The so-called "motive molecules" are basically the hormones of our chemical environment, responsible for handling the overall mood of the deity which rules over its internal universe.
As we can tell from the examples illustrated so far, it is not so hard to expand the universal laws of game design into forms that are physically implementable. The last remaining question is whether this revelation will lead to commercially viable solutions by letting our end products interact with the ecosystem in profitable ways.
And my answer is, "Yes, definitely". Since it is now proven that the generic interspecies gaming model can be implemented within pretty much any computing device (e.g. PC, phone, console, etc) as well as other physical analogues, the rest of the technical problem only lies on that of introducing an appropriate user interface for whichever target audience we are aiming at. If the player is a cow in a cowshed, for instance, we will need to mount a screen for the cow to look at, a pressure sensor which will fire a signal when licked by the cow, and a dispenser which will "reward" the cow by releasing a piece of bite-sized fodder whenever the cow conducts a peculiar licking activity which biologically induces it to produce more milk than usual.
While this specific cow example may not be economically viable in reality, we should also remind ourselves that there are countless other potentially lucrative scenarios we can venture to imagine in various industries as well as the nature itself. After all, we are all already aware an age-old human activity which can be described as an "interspecies game"; it is called "fishing". A person throws a bait into the surface of a lake with the help of a fishing rod, which effectively converts the whole habitat into a multiplayer gaming arena (aka "MOBA") in which each fish is a player who participates in the game by actively competing with other fish to spot the bait first and eat it, for the purpose of rewarding itself with the extra energy (calories) it is expected to obtain by the act of grabbing the bait. In this case, the bait is the "resource" of each fish player, and any other fish is its "obstacle". One could say that the fisher basically turned the whole lake into a gaming area by artificially assigning the two opposing properties ("resource" and "obstacle") to the lake's atomic constituents.
(Will be continued in Volume 14)
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service