
Author: Youngjin Kang Date: 2023.04
(Continued from Volume 9)
When we think about the nature of the word "game", we often come to the conclusion that a game is a network of goals and their respective actions. The player (or any equivalent gameplay agent) recognizes a list of goals to pursue, and endeavors to complete these goals by carrying out a list of actions.
Actions do not come for free, however, since it is obvious that the absence of cost would enable the player to achieve goals without even the slightest allusion of difficulty, which is clearly an undesirable trait for an interactive medium such as a game. Therefore, actions which are part of the process of fulfilling one's in-game goals should involve exchanges of entities that are limited in quantity.
In the previous volume, we saw the possibility of modeling the concept of exchange in terms of potentials and their respective energy particles. Energy descends the stream of potentials from high to low energy levels, as suggested by the laws of nature we are capable of witnessing every day. And as long as we suppose that an active gameplay agent (e.g. player) is able to temporarily add a set of new potentials to the system for the purpose of transferring a set of energy atoms in a certain way for a brief moment, it must be logically sound for us to imagine that the agent triggers an action by applying a specific set of potentials, waiting for a moment to let the energy atoms rebind themselves, and then destroying the applied potentials. Such an act of application can be referred to as "motivation", and the act of the subsequent destruction can be referred to as "demotivation", for it is sensible to consider a voluntary action as an event which requires the presence of a motive.
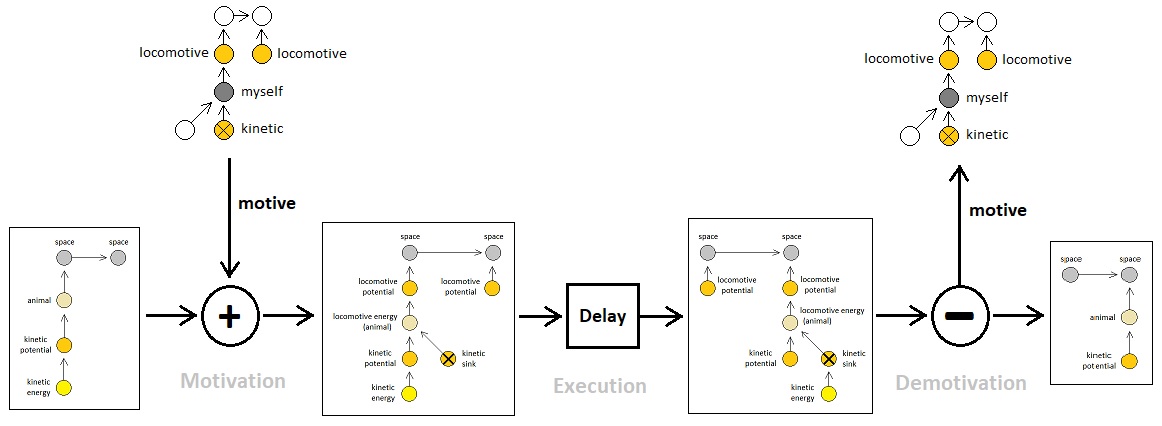
A process of motivation and its subsequent cancellation (i.e. demotivation), which represents the start and end of an agent-driven action, signifies a momentary jump of energy from one spot to the other in a highly discrete manner (like a single drop of water which falls from a briefly lifted tap), as opposed to a continuous flow of energy which occurs through a long descending series of persistent potentials.
Such a discrete instance of energy transfer is a component of an exchange, since a singular exchange is defined in terms of quantitative changes that are impulsive rather than continuous. And since any specific in-game action (e.g. "Collect this gem", "Kill this enemy", etc) can ultimately be broken down to a sequence of atomic movements and each of them is a constituent of an energy transfer (as long as we suppose that every atom is some kind of energy particle), we can say that any in-game action is made out of exchanges.
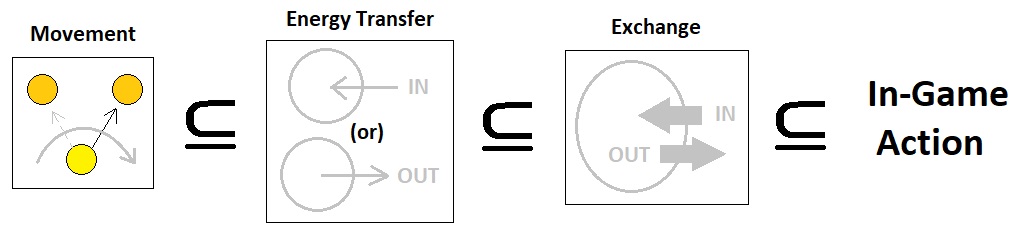
We have seen that a momentary energy transfer is realized by a process of motivation and demotivation, which respectively correspond to the addition and removal of a specific set of potentials. It seems convenient, therefore, to fancy that such a set of potentials and the way in which they get added, as a whole, constitute the definition of the term "motive"; that is, an agent triggers an energy transfer by adding a motive, and terminates it by removing the motive that was added.
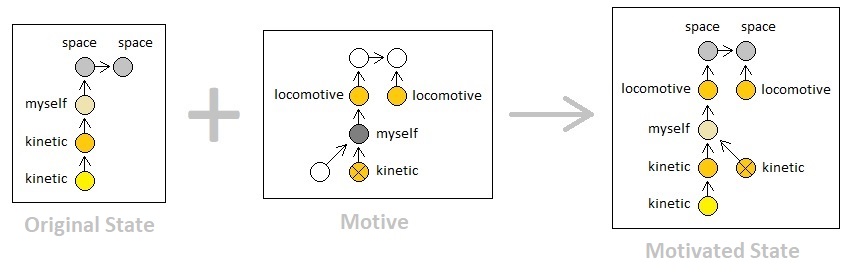
And depending on the type of energy transfer, there could be different types of motives each of which has its own unique molecular structure. It is not so rash to imagine that one can conceive a wide spectrum of chemical laws out of this.
But before delving directly into this vast pond of possibilities, let us go back to the initial line of reasoning which gave birth to the idea of energies, potentials, and their respective laws of interaction. Initially, it all began with the problem of identifying atoms that are resources as opposed to atoms that are obstacles. And based on the definition that a resource is something which is capable of giving energy to the observer and an obstacle is something which is capable of taking energy away from the observer, I have suggested the existence of special atoms called "potentials" as well as energy particles which automatically ride upon and traverse them from higher levels to lower levels, as means of fully explaining the causal origin of resources and obstacles.
From the laws of nature and their quantitative patterns we have sensed so far, one can fairly easily imagine that an atom could either be identified as a resource or an obstacle depending on the type and level of a potential it happens to possess.
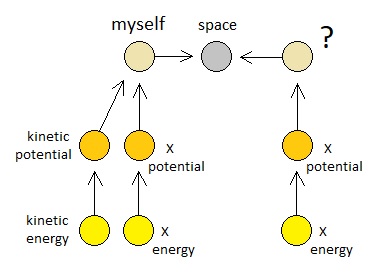
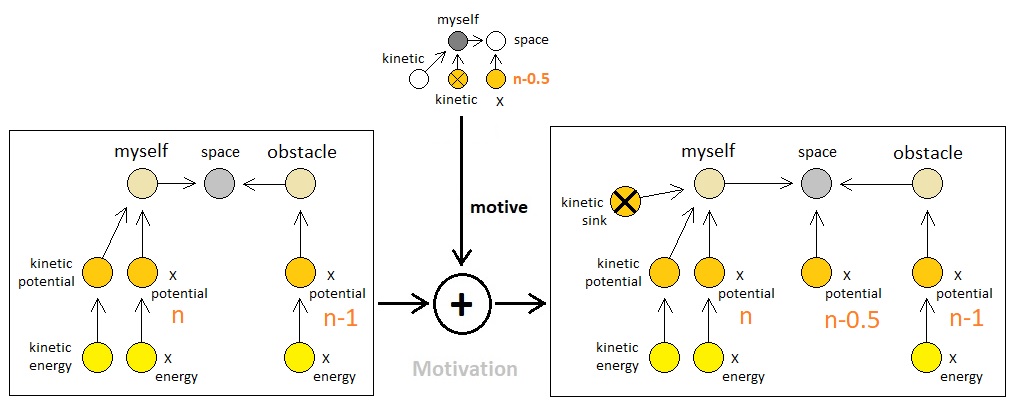
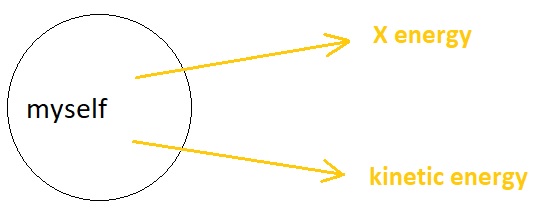
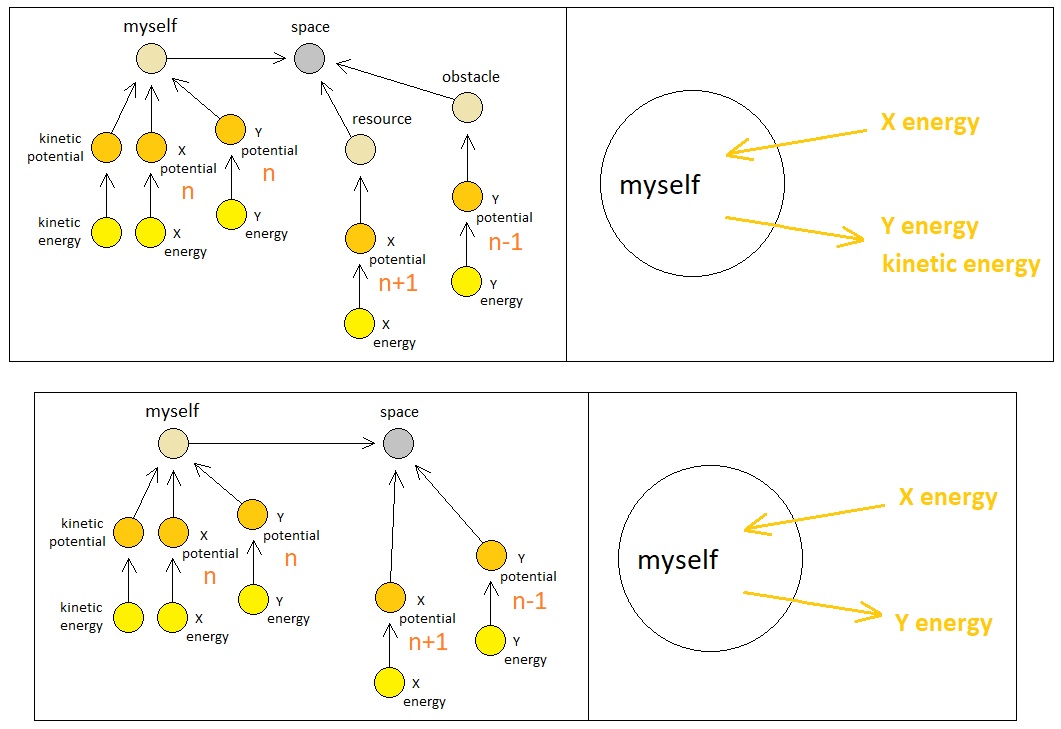
Let us suppose that the observer has two potentials (of type "X" and "kinetic") and their corresponding energy particles. The idea is, the observer is interested in gaining new X energy atoms by spending its own kinetic energy atoms; so any event which involves the incoming of X energy and outcoming of kinetic energy is a desirable form of exchange for the observer.
As long as the aforementioned supposition holds, we can safely assume that any atom which is close enough to the observer and is carrying a potential of type X may be able to let the observer issue an exchange which aligns with such an interest, depending on the potential's relative energy level. Triggering an exchange which involves a transfer of X energy between such an atom and the observer, from the observer's side of actions, can be carried out by means of motivation - that is, by adding a temporary X potential between the two participants of the exchange, which works as a bridge that connects the two roads of transportation (because an energy atom cannot jump across potentials that are separated by distances greater than 1).
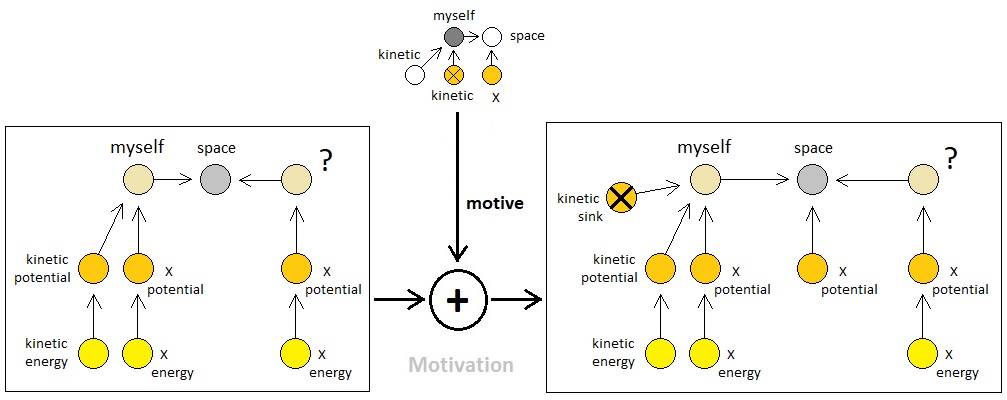
Since we do not want the player to be able to create a perpetual motion machine from which one can extract infinite energy, it must be the case that every observer-issued energy transfer requires some form of cost on the observer's side (aka "transaction fee"). Therefore, it is reasonable to expect that any process of motivation must simultaneously add a kinetic sink which drains one of the kinetic energy particles of the observer whenever it adds a potential that has at least a bit of possibility of bringing extra energy of another type into the observer's body.
And the difference between the energy level of the observer's X potential and that of the neighboring atom's X potential, by nature of the directionality of energy transfer (i.e. which always points from high to low level), can be said to either bear the possibility of donating X energy to the observer or stealing X energy from the observer upon exchange, depending on whether its value is positive or negative.
For example, let us say that the observer's X potential has level "n" and that the other atom's X potential has level "n+1". In this case, the observer is able to create a continuous ramp of X potentials that is tilted inwards by adding an X potential between itself and the other atom with a level that is the average value between "n" and "n+1" (i.e. "n+0.5"). Such a creation, of course, comes with a bit of kinetic energy cost.
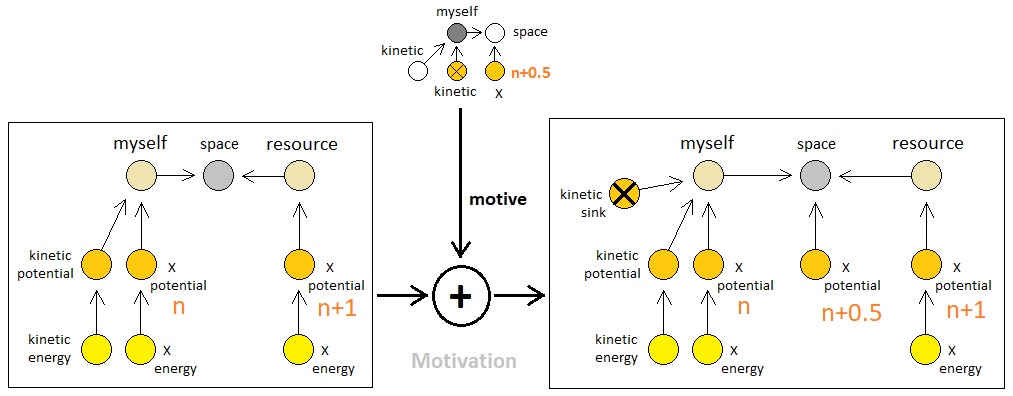
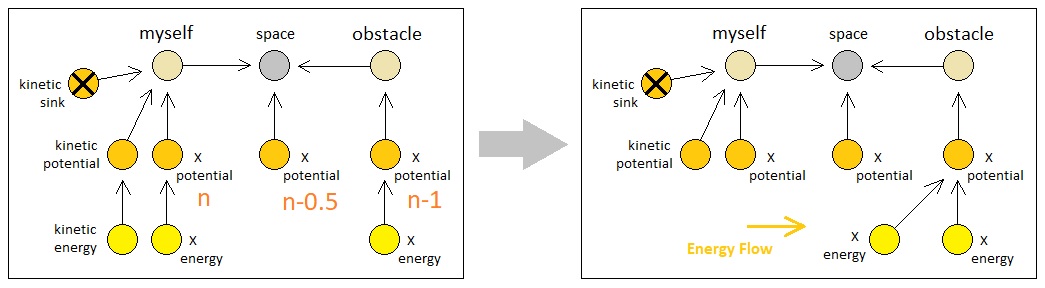
If the other atom's X potential contains an X energy particle, then, it will automatically flow into the observer's X potential during the span of 2 discrete time steps (First step transfers the particle from the other atom's X potential to the local space's X potential, and the second step transfers the particle from the local space's X potential to the observer's X potential). If the other atom's X potential does not contain an X energy particle, on the other hand, such a flow will fail to occur.
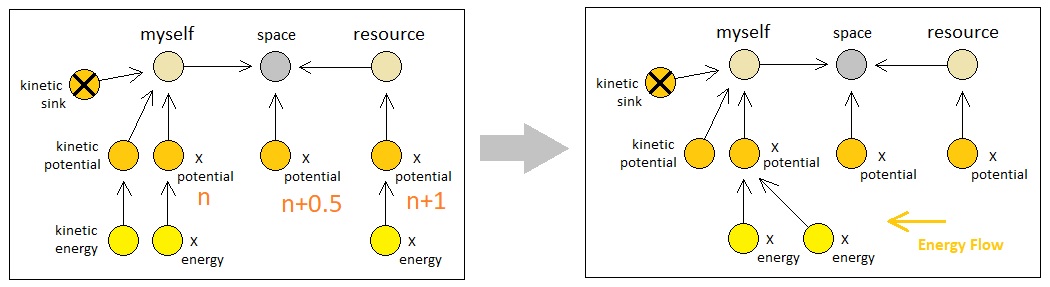
The thing is, though, that the other atom can still be considered as having some probability of giving off X energy particles to the observer as long as its own possession of X energy particles is either not known by the observer or simply undefined. This enables us to identify the atom as a "resource" solely based upon the characteristics of its X potential and not its inner content.
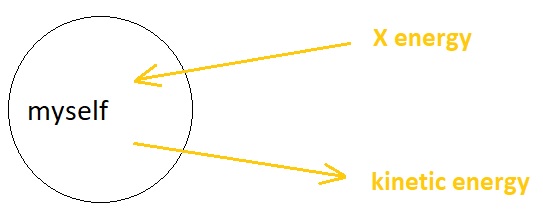
The aforementioned interaction, which is basically an exchange between an X energy particle and a kinetic energy particle from the observer's perspective, can be illustrated in the form of a diagram shown below. X energy enters the "inside" of the agent's body, and kinetic energy gets released to the "outside" of the agent's body in a strictly simultaneous fashion.
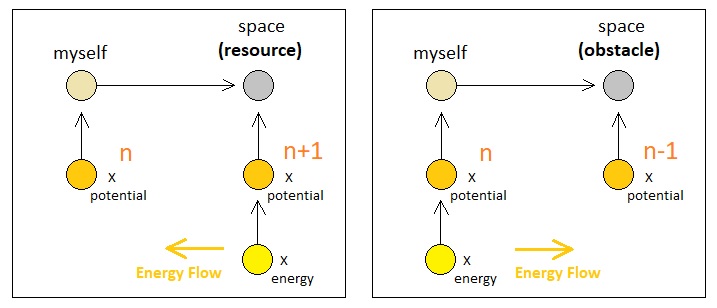
What if the other atom's X potential has level "n-1", a value that is less than "n"? In this opposite scenario, what we are expected to witness is that there will be no direct way of establishing a bridge between the observer and the other atom in a way in which the other atom's X energy particle can manage to travel towards the observer on its own (since an energy atom does not voluntarily climb up a staircase of energy levels).
Instead, any presence of a bridge will induce the observer's X energy particle (if there is any) to move towards the other atom due to the fact that the ramp of energy levels is, in this case, inclined towards the other atom instead of the observer. This makes the other atom qualify as an "obstacle"; it has a tendency to steal energy from the observer as soon as the right condition (i.e. bridge) is given.
This opposite kind of interaction, too, can be classified as an exchange, although its outcome may be deemed far unfairer than that of an interaction with a resource. An exchange with an obstacle almost always involves far more loss in energy than gain (if there is any gain at all), and therefore one might question the legitimacy of the above scenario by saying, "Wait, why on earth would the observer ever want to lay a bridge between itself and an obstacle, if it cannot be expected to bring any benefit at all?"
And such a point of reasoning is indeed valid, except that there are many other probable causes which may trigger the same exact sort of exchange as the one depicted above. For instance, the obstacle itself could be an active agent which, upon arrival of the observer, recognizes it as a resource (because n is greater than n-1) and thus puts an "n-0.5" under the shared local space in order to extract energy from the observer. Also, the observer itself may be having a status condition which automatically induces it to lose X energy by laying a bridge to whichever obstacle it encounters (thermal dissipation could be an example of this).
There may as well be cases where the observer's local space itself possesses a potential by default. In such a case, one may say that it is the spatial region itself which can be identified as either a resource or an obstacle, depending on whether its potential's energy level is greater than or less than that of the observer's. If a space is either a resource or an obstacle, it is not hard for us to imagine that an energy transfer between itself and the observer will occur automatically (without even having to add a motive) as soon as the observer enters the space. This is because the distance between an atom and its binding target is only 1, which is a sufficiently small distance for an energy particle to jump between its potential and the other's potential.
Things are not always black and white, however. There could be a condition in which the observer's local space is being shared by both a resource and an obstacle, or there could be a condition in which the local space itself exhibits both the behavior of a resource and the behavior of an obstacle by containing potentials of both kinds. Such ambivalent circumstances fit the conventional definition of the word "exchange"; an agent may choose to be involved in an exchange not necessarily because it is bound to result in either strict gain or strict loss, but rather because it allows the agent to sacrifice one type of energy for the acquirement of another.
The purpose of the theoretical formulation which I have been undertaking so far is to prove that it is possible to come up with dynamic patterns of motivation (hence their underlying narratives) without having to devise a long list of arbitrary rules. Agents which comprise the gameplay universe, whether they be physical or abstract, can be expressed in terms of atoms, and their energy level differences give them reasons to motivate themselves to modify the arrangement of potentials for the purpose of gaining desired energy particles while getting rid of those that are unnecessary.
It is time for us, however, to go back to the initial example of the complexity of psychological phenomena which seemed to prevent the designer from quantitatively modeling an agent's volitional tendencies. The wizard I mentioned in volume 8, who possesses a mysterious desire to convert everything into a donut, initially gave an impression that the origin of his motivation is only explicable through the context of a lore - that is, a rich background story which illustrates the reason why he is so obsessed with donuts in particular.
To be honest, I do concede that it is not quite feasible to fully explain the ultimate causal root of the wizard's strange attachment to donuts solely by means of pure mathematical definitions (It might eventually turn out be possible, yet approaching such an objective seems to be too daunting a task for now). However, it should also be noted that at least the underlying motive of the wizard's donut-summoning behavior itself can be abstracted out into an indivisible entity (i.e. an "atomic idea"), which can then fit into the mechanical inner workings of the system as a discrete building block.
Let us suppose that this donut-loving wizard is an atom which possesses a special kind of energy called "magic energy". He stores his own magic energy (aka "mana") inside his supernatural battery called "magic potential", and whenever he casts a spell, this battery discharges a bit and consumes 1 magic energy particle. Let us also imagine that this wizard is currently standing right in front of an atom that is not a donut (aka "non-donut"), and that he desperately wants to transform this atom into a donut. How shall we explain the nature of motivation involved in here, as well as its subsequent result?
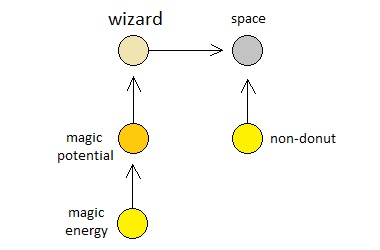
Unlike the previous example which demonstrated the problem of identifying resources and obstacles, this one is a bit tricky because it apparently involves a conversion of one type of atom to another. Since potentials and their resultant paths of energy flow only explain the nature of motion and not the internal chemistry of atoms themselves, one might be tempted to say that the only way to model a process of transformation is to represent both a donut and a non-donut as a molecular structure that is made up of multiple atoms, whose internal rearrangement allows the whole structure to be renamed from "non-donut" to "donut", or vice versa. However, there is a simpler way.
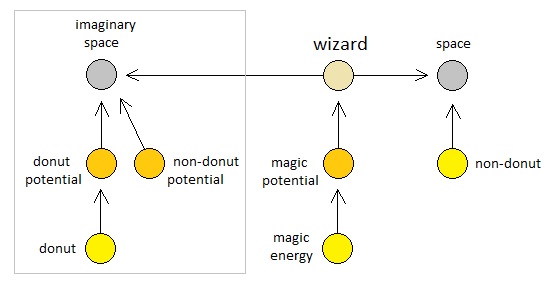
In volume 2, I mentioned that any object which "exists" can be thought of as being contained inside a real space, whereas any object which "does not exist" can be thought of as being contained inside an imaginary space. Based upon this hypothetical pair of definitions, I claimed that the process of creating an object is an equivalent of moving it from imaginary space to real space, and that the process of destroying an object is an equivalent of moving it from real space to imaginary space.
Since the process of converting a non-donut to a donut is the same thing as destroying a non-donut and creating a donut at the same time, we can say that the wizard is capable of transforming a non-donut into a donut as long as he is capable of simultaneously moving a non-donut from real space to imaginary space while moving a donut from imaginary space to real space. This will be possible if the wizard's current position in space not only belongs to a real space, but also to an imaginary space within which both a non-donut potential and a donut potential coexist in parallel. In a way, we may call the wizard a "semi-mythical" being due to the fact that he is situated within the area of intersection between the real and imaginary parts of the universe. And based upon this notion, one may fancy that many of the paranormal activities, such as shape-shifting, are directed by agents who reside in the zone of limbo between the borderline of reality and the borderline of imagination.
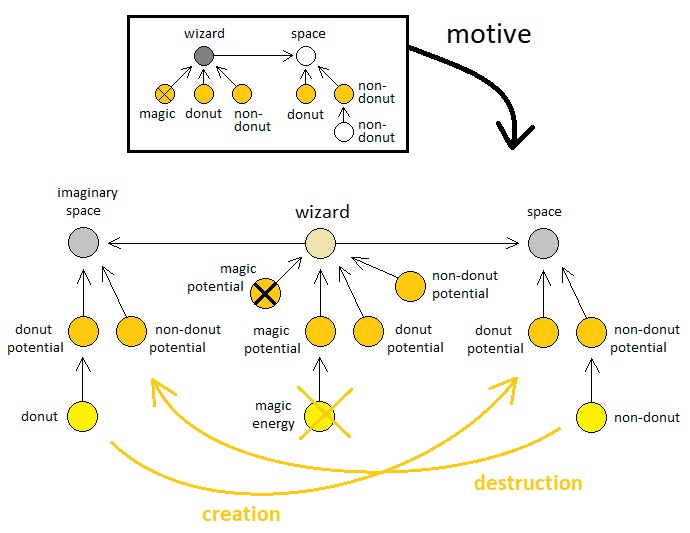
With the application of an appropriate motive, then, the wizard is able to convert any nearby non-donut into a donut by means of inducing both the non-donut and an imaginary donut to fall down through their own streams of descending potentials. The precise mechanic of this motivational procedure, which may as well be identified as a spell-casting activity, is illustrated above.
At this point, one might ask, "Where does the motive itself come from? Surely it cannot just pop out of nowhere without any apparent physical cause." My answer would be that the atoms which constitute the motive themselves are motivational energy particles which follow their own downward paths of "motivational potentials". Such potentials are part of the wizard's (i.e. motive-creator's) inner mind and thus are completely invisible from a physical standpoint. And any change in one's motives is caused by changes in the shapes of such downward paths, which are themselves results of motivations that are applied from the external environment. In other words, motives which naturally occur from the physical surroundings continuously modify the arrangement of potentials within the observer's mind, and motives which occur from the observer's mind continuously modify the arrangement of potentials within the physical surroundings. This is a perpetual back-and-forth cycle of motivation which happens between the inside and outside of the observer's existential boundary.
In the next volume, we will see how the model developed so far applies to a variety of in-game activities, as well as how it promises to simplify down the overall design process.
(Will be continued in Volume 11)
Previous Page Next Page
© 2019-2025 ThingsPool. All rights reserved.
Privacy Policy Terms of Service