
Author: Youngjin Kang Date: June 10, 2024
(Continued from Part 7)
Let us imagine that we are in a biscuit factory, staring at a conveyor belt which has biscuits on it.
The belt does not have to be fully loaded with biscuits, however. It may as well have empty slots, as well as those that are occupied by other types of objects such as cookies, tarts, or homemade pot pies.
Each slot carries its own identifier such as ID, ID², or ID³, and we have the right to assign anything to it, including emptiness itself (which is represented by 0). An example is shown below.
conveyorBelt = biscuit ID² + dough ID³
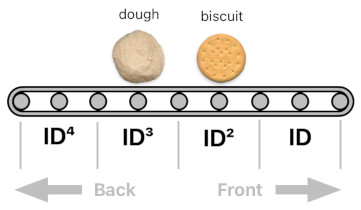
This belt has a biscuit on the second slot (ID²) and a piece of dough on the third slot (ID³). The first slot (ID) is empty (= 0), so it does not even appear in the formula.
For simplicity's sake, though, I will ignore the sheer variety of stuff with which the conveyor belt could be filled up for now and solely focus on its rudimentary mechanics. Suppose, for a moment, that we only have a biscuit on the second slot (ID²) and absolutely nothing else.
conveyorBelt = biscuit ID²
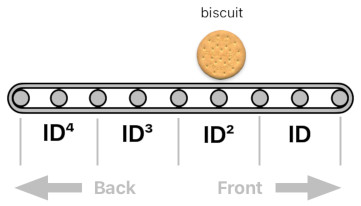
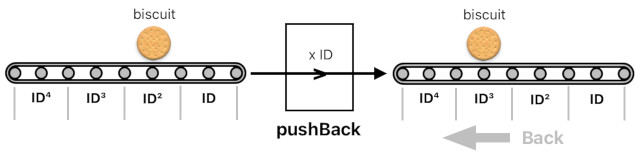
What is going to happen if we multiply the formula by ID? Assuming you know how to multiply, I would say that the biscuit's identifier (ID²) will turn itself into ID³ because ID² x ID = ID³. This is the same thing as pushing the biscuit to the back by one slot.
pushBack(biscuit ID²) = (biscuit ID²) ID = biscuit ID³
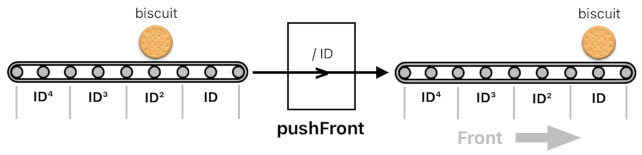
The inverse operation is also possible. You can push the biscuit to the front by dividing the formula by ID instead of multiplying.
pushFront(biscuit ID²) = (biscuit ID²) / ID = biscuit ID
The ability to push things in both directions is not limited to the case of a single biscuit. If there are multiple objects on the conveyor belt, multiplication by ID will push all of them simultaneously to the back. Similarly, division by ID will push all of them simultaneously to the front.
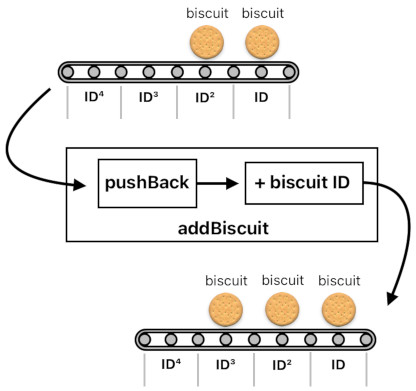
Let us revisit the previous two functions called "addBiscuit" and "subtractBiscuit". In these two functions, we were dealing with a bunch of biscuits and their distinct identifiers (e.g. ID, ID², ID³).
In order to add a new biscuit to the belt, what should we do? If the frontmost slot (ID) is empty, we can simply add "biscuit ID" to the formula to fill it up with a biscuit. If the slot is not empty, however, adding "biscuit ID" to the formula without any prior action will basically "mix" the new biscuit with the existing object, subsequently generating a weird mixture.
Therefore, we must first push everything to the back in order to make room for the new biscuit. Once we do that, we will be able to safely add "biscuit ID" to the conveyor belt without worrying about accidentally mixing things up.
addBiscuit(conveyorBelt) = biscuit ID + conveyorBelt ID = biscuit ID + pushBack(conveyorBelt)
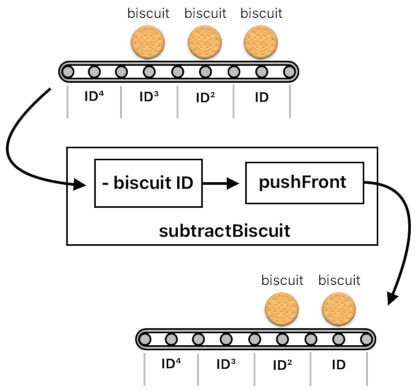
What about subtracting a biscuit? If we presume that the frontmost slot is already occupied by a biscuit, we will be able to tell that subtracting "biscuit ID" from the formula will neatly get rid of an existing biscuit from the conveyor belt. Then, since somebody might want to remove yet another biscuit later on, we should probably push everything to the front so as to enable subsequent acts of subtraction.
subtractBiscuit(conveyorBelt) = (conveyorBelt - biscuit ID) / ID = pushFront(conveyorBelt - biscuit ID)
The notion that we ought to "push things to the front after removing the frontmost element" is not just something I contrived out of nowhere. When you grab a gun (semiautomatic pistol) and fire it once, what does it do? It first destroys the uppermost bullet by hitting its ass with a rigid rod, and then pushes the rest of the bullets upward to fill the gap. Think of the "subtractBiscuit" function as the act of firing a biscuit-gun.
The real problem, though, resides in the fact that I am making a bold assumption here which may not always be the case.
If the belt's frontmost slot were occupied by a biscuit, we would definitely be able to use the "subtractBiscuit" function without any trouble. If the slot were either empty or occupied by something else, however, we would be in trouble because applying the "subtractBiscuit" function to such a case is an equivalent of merging an anti-biscuit (i.e. "-biscuit") with whatever is sitting on the frontmost slot.
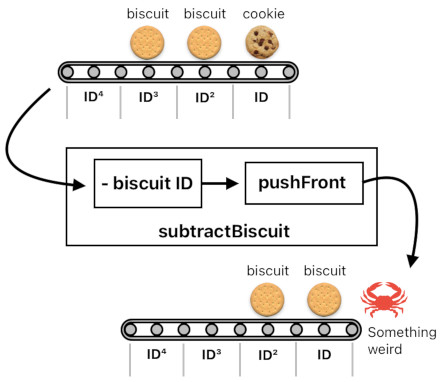
In order to prevent such a calamity, we must check the current status of the conveyor belt before fiddling with it. This "checking" part, when correctly implemented, will prevent us from facing undesired consequences.
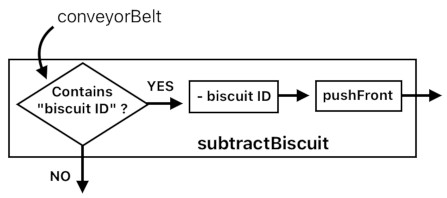
How shall we do that, in the case of the "subtractBiscuit" function? The first step is to decide which condition we ought to check, and the second step is to decide what to do when such a condition is either satisfied or dissatisfied.
In other words, we need a conditional statement in our function.
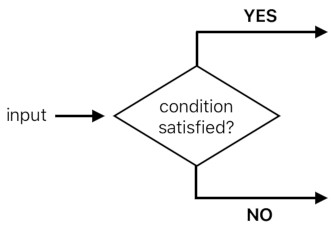
A conditional statement allows us to choose which of the two pathways we must follow. If the given condition is satisfied, we will follow the "YES" path. If not, we will follow the "NO" path.
In our "subtractBiscuit" function, the condition we want to check is whether the conveyor belt's frontmost slot has a biscuit or not. Algebraically, it is the same thing as saying whether the formula contains the "biscuit ID" term or not.
If this condition is met, we will proceed to remove "biscuit ID" from the belt. This is our "YES" path.
Otherwise, we must leave the belt as it is without changing anything. This is our "NO" path.
CONDITION: Does conveyorBelt contain "biscuit ID"?
IF "YES": subtractBiscuit(conveyorBelt) = pushFront(conveyorBelt - biscuit ID)
IF "NO": subtractBiscuit(conveyorBelt) = conveyorBelt
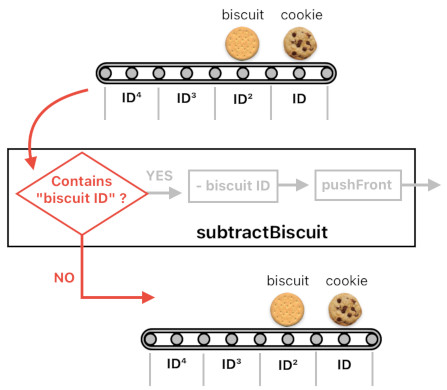
What shall we do if the conveyor belt's frontmost slot is occupied by a cookie instead of a biscuit? The answer is pretty straightforward because we now know what the condition is. The formula does not have "biscuit ID" in it, so we will do nothing and simply return the original conveyor belt.
conveyorBelt = cookie ID + biscuit ID²
subtractBiscuit(conveyorBelt) = conveyorBelt
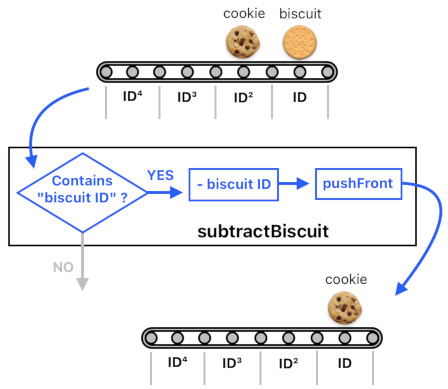
What shall we do if the conveyor belt's frontmost slot is occupied by a biscuit? Since the formula does indeed have "biscuit ID" in it, we will continue on with our usual biscuit removal process.
conveyorBelt = biscuit ID + cookie ID²
subtractBiscuit(conveyorBelt) = pushFront(conveyorBelt - biscuit ID)
So far, quite a number of things have been demonstrated. We now have a method of keeping multiple objects together in one place (i.e. conveyor belt), as well as a method of adding, removing, and modifying them in a selective fashion, with the help of conditional statements such as: "Is the fourth slot of this conveyor belt empty?".
All these techniques, with a bit of additional insight, allow us to build any sophisticated system we may dare to imagine.
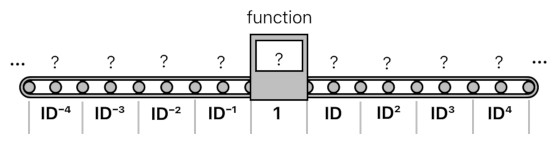
In order to prove such a claim, let me suppose that our conveyor belt is infinite in length - that is, its number of slots is unbounded. In the middle, we have a slot which has "1" as its identifier (because it is the 0-th power of ID, which equals 1). On the right side, we have slots identified by positive powers of ID. On the left side, we have slots identified by negative powers of ID.
conveyorBelt = ... + (?)ID⁻³ + (?)ID⁻² + (?)ID⁻¹ + (?) + (?)ID + (?)ID² + (?)ID³ + ...
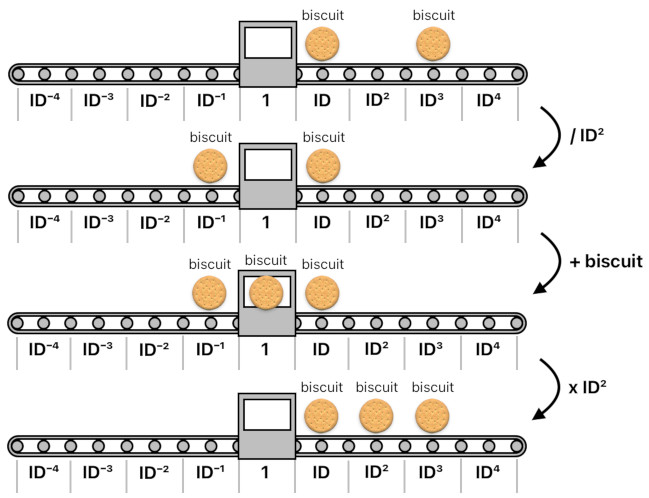
And let me also suppose that there is a function called "addBiscuitAt" which adds a biscuit not necessarily at the frontmost slot of the conveyor belt, but at any given slot (i.e. the one whose identifier is "slotID").
addBiscuitAt(conveyorBelt, slotID) = (biscuit + conveyorBelt / slotID) slotID
The way this function operates may look a bit strange, but it is not too hard to comprehend. Think of it as a machine which sits at the center of the conveyor belt. Dividing the formula by "slotID" pushes all the slots in the way in which it will bring the designated slot to the center. The machine, then, adds a biscuit, and then multiplies the formula by "slotID" to push all the slots back to their original locations.
This 3-step procedure, as a result, modifies only the given slot (i.e. the one whose position is "slotID") and leaves all other slots untouched.
An example usage of this function is displayed below.
conveyorBelt = biscuit ID + biscuit ID³
addBiscuitAt(conveyorBelt, ID²) = (biscuit + conveyorBelt / ID²) ID²
In addition, there may also be myriads of other functions which are designed to access and/or modify any arbitrary slots in this infinite conveyor belt, such as "subtractBiscuitAt(...)", "moveBiscuitTo(...)", and so on. With the help of such functions, we will be able to do anything a computer can do. Why? Because what I just portrayed here is essentially what people call "Turing Machine".
The world of math is one vast imaginary computer. Our conveyor belt is the computer's memory, and our functions are its machine instructions (aka "programs").
(Will be continued in Part 9)
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service