
Author: Youngjin Kang Date: June 7, 2024
(Continued from Part 6)
It has been supposed that a biscuit is a combination between 10 temperature particles and 2 sweetness particles.
biscuit = 10 temperature + 2 sweetness
Here is something tricky, though. What if there are two biscuits instead of one? Shall we just multiply the biscuit by 2, so as to express the fact that there are two copies of it? But if we do that, the numbers will soon show us that the result is a mixture of temperature/sweetness particles that are twice as many as before, which is something unknown to us.
2 biscuit = 2 (10 temperature + 2 sweetness) = 20 temperature + 4 sweetness
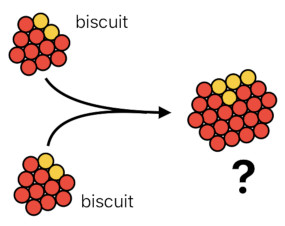
When someone says, "There are two biscuits", one does not simply mean that the ingredients of these two biscuits are put together at the same location. What the person really means is that there are two whole separate biscuits, existing independently from each other.
Therefore, we need some way of distinguishing one biscuit from the other whenever we are dealing with two biscuits instead of just one. How shall we accomplish such a goal?
One thing that is for sure is that each biscuit must possess its own identity (aka "ID") in order to be able to distinguish itself from others. If we suppose that there are two special variables called "ID1" and "ID2", for instance, we will be able to use them to uniquely identify two biscuits.
Assignment of an identifier can be done by means of multiplication. If you have a biscuit, you can assign the identifier "ID1" to it by simply multiplying it by ID1. Likewise, you can assign the identifier "ID2" to another biscuit by multiplying it by ID2. Once you do that, you can safely combine the two results together and still ensure that these two biscuits are separate objects, as well as that they are just being "placed together" instead of being merged into one grotesque sort of concoction.
biscuit ID1 + biscuit ID2
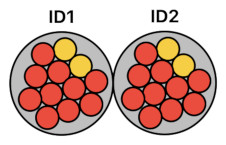
As the formula above tells us, each identifier prevents its respective biscuit from being merged with the other, due to the fact that there is no way for us to simplify the expression "biscuit ID1 + biscuit ID2" to a single term. Since ID1 and ID2 are variables instead of plain numbers, we are unable to fuse the term "biscuit ID1" and the term "biscuit ID2" together into a single numerical value.
This works well so far, but here is a problem of scalability. If I have 3 biscuits instead of just 2, what should I do to keep these 3 things separate from one another instead of letting them fuse into one?
Indeed, a straightforward solution is to introduce the third identifier called "ID3" and proceed to assign it to the third biscuit via multiplication.
biscuit ID1 + biscuit ID2 + biscuit ID3
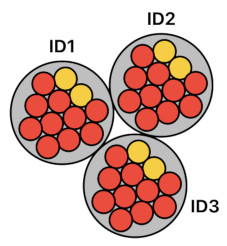
As you may have noticed, however, it implies that we will be obliged to come up with a brand new identifier whenever we decide to add yet another biscuit to the formula.
What if we want the fourth biscuit? Oh, we will need "ID4" to make sure that this fourth biscuit is different from the previous three. What if we want the fifth biscuit? Oh, of course, we will need "ID5" to make sure that this fifth biscuit is different from the previous four. And so on.
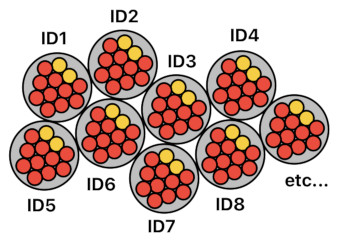
This is obviously unsustainable. If we need a truckload of identifiers just to represent a truckload of biscuits, there must be something wrong here.
Fortunately, there is one little trick you can use to solve such a problem. Suppose that there is a variable called "ID" which can be used as a unique identifier. One important point to realize is that, since "ID" is just an arbitrary variable, we can multiply it by itself (i.e. ID ID) to create a whole new unique identifier. This method of generating identifiers may continue on and on, like the examples shown below.
ID1 = ID
ID2 = ID ID
ID3 = ID ID ID
The first identifier is the result of multiplying ID once, the second identifier is the result of multiplying ID twice, and so on, which means that the n-th identifier is the same thing as multiplying ID n times. If we use this pattern to keep three biscuits separate from one another, it will look like:
biscuit ID + biscuit ID ID + biscuit ID ID ID
Since repeating the same multiplication is basically what exponentiation is in mathematics, the expression above will be simplified as:
biscuit ID + biscuit ID² + biscuit ID³
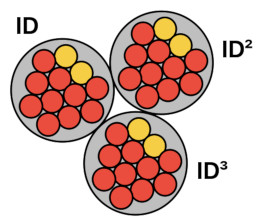
The first identifier is ID itself, the second identifier is ID-squared, and the third identifier is ID-cubed.
So, if you ask the first biscuit, "Show me your identification card, please!", he will show you a thin stick that is ID-meters long. If you ask the second biscuit the same question, this second gentleman will show you a square sheet of paper with sides that are ID-meters long. If you ask the third, he will show you a cube with edges that are ID-meters long. This is how you allocate separate identities to these 3 biscuits; each of them is identified by the number of dimensions of his ID card.
The role of ID, ID², and ID³ is to make their corresponding terms (biscuits) unique, so that they will not mix with each other. If you try expanding the formula like the following:
biscuit ID + biscuit ID² + biscuit ID³ = (10 temperature + 2 sweetness) ID + (10 temperature + 2 sweetness) ID² + (10 temperature + 2 sweetness) ID³ = 10 temperature ID + 2 sweetness ID + 10 temperature ID² + 2 sweetness ID² + 10 temperature ID³ + 2 sweetness ID³
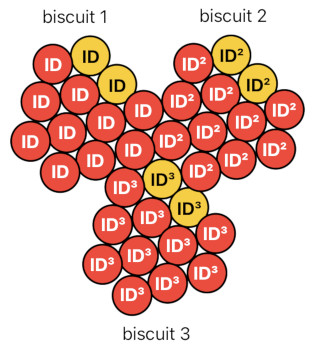
You can clearly see here that the temperature particles of the first biscuit are separate from those of the second and third, as well as that the sweetness particles of the first biscuit are separate from those of the second and third. This is because every single particle of a biscuit is endowed with the biscuit's own identity.
What if you want to create a new biscuit? This, too, can be accomplished fairly easily based upon a simple algebraic trick. Since each biscuit's unique identity is solely determined by the number of times it has been multiplied by the variable called "ID", all you have to do to introduce a new biscuit to the scene consists of two steps: (1) Multiply the whole algebraic expression by ID, and (2) Add "biscuit ID" to the resulting expression.
If we suppose that there is a function called "addBiscuit" which carries out the procedure I just mentioned, it will look like the following:
addBiscuit(originalBiscuits) = biscuit ID + originalBiscuits ID
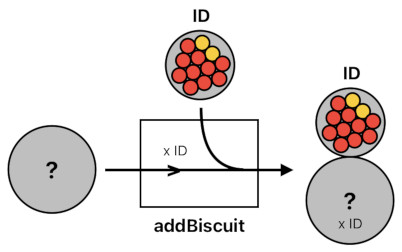
The "addBiscuit" function receives the original list of biscuits (i.e. "originalBiscuits") as the input and produces the augmented list of biscuits as the output. If we originally had only 2 biscuits, "originalBiscuits" would be expressed as:
originalBiscuits = biscuit ID + biscuit ID²
The output, then, would be:
addBiscuit(originalBiscuits) = biscuit ID + (biscuit ID + biscuit ID²) ID = biscuit ID + biscuit ID² + biscuit ID³
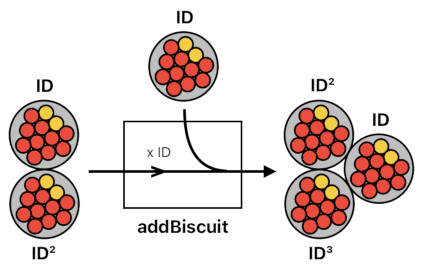
This is exactly as expected. Since we added a biscuit to the original list of 2 biscuits, we now have 3 biscuits which are being identified by ID, ID², and ID³.
The converse process is equally feasible. Just like we are allowed to add a biscuit to the group, we must also be allowed to subtract an existing biscuit from the group. Imagine that there is yet another function called "subtractBiscuit" which does exactly what the "addBiscuit" function does in reverse (because subtracting is the opposite process of adding). That is, whenever it receives an input, it: (1) Subtracts "biscuit ID" from the given algebraic expression, and (2) Divides the resulting expression by ID.
subtractBiscuit(originalBiscuits) = (originalBiscuits - biscuit ID) / ID
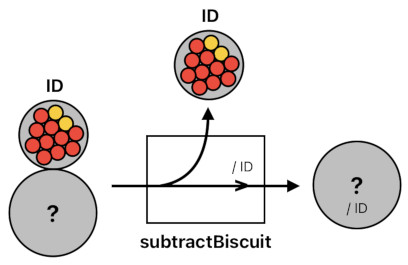
The "subtractBiscuit" function subtracts "biscuit ID" instead of adding it because subtraction is the inverse of addition, and divides ID instead of multiplying it because division is the inverse of multiplication. Also, this function runs the two arithmetic steps in the reverse order with respect to that of the "addBiscuit" function.
So, if we suppose that there were originally 3 biscuits,
originalBiscuits = biscuit ID + biscuit ID² + biscuit ID³
Subtracting a biscuit from it will exhibit the result below:
subtractBiscuit(originalBiscuits) = (biscuit ID + biscuit ID² + biscuit ID³ - biscuit ID) / ID = (biscuit ID² + biscuit ID³) / ID = biscuit ID + biscuit ID²
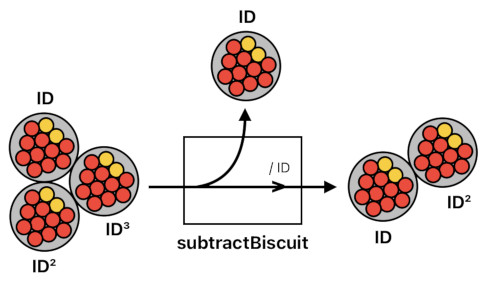
This means that subtracting a biscuit from the original list of 3 biscuits will give us an updated list which only contains 2 biscuits (i.e. One with the identifier "ID", and the other one with the identifier "ID²").
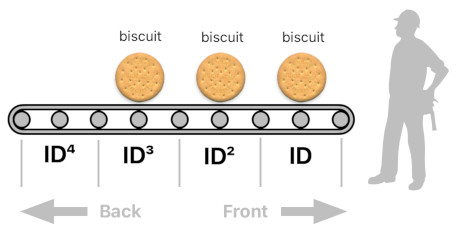
A handy way to picture in our minds what is really going on is to imagine that we are inside a factory's assembly line, looking at a conveyor belt which carries a queue of biscuits. The conveyor belt consists of a number of slots, each of which can be occupied by a biscuit.
If we assume that the first slot is identified by "ID", the second slot is identified by "ID²", the third slot is identified by "ID³", and so forth, we will be able to declare that each of these identifiers essentially refers to the position of the slot with respect to the end of the belt.
(Will be continued in Part 8)
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service