
Author: Youngjin Kang Date: May 21, 2024
(Continued from Part 1)
A number itself does not mean anything. A number which indicates a quantity of something we can see, hear, smell, or touch, on the other hand, does mean something.
In the previous chapter, I mentioned that a function is a machine which receives a thing called "input" and emits another thing called "output". A function does not necessarily receive everything we can possibly imagine, though; it is usually expected to accept only a certain category of things as inputs, and emit only a certain category of things as outputs.
It has also been noted that, for the purpose of simplicity, it is sensible to group things of interest in the form of an ordered sequence. This enables us to refer to them with numbers instead of arbitrary names.
The "bake" function is a machine which converts a piece of dough (input) into a biscuit (output). However, we are also aware that there are different types of dough from which a whole variety of baked products can arise, such as cookie dough, shortbread dough, scone dough, and so on. The "bake" function must take all these possibilities into account, since the word "bake" does not confine itself to the process of baking nothing but a tasteless hardtack.
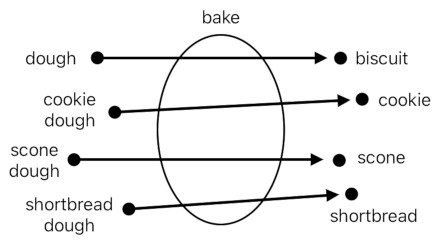
And it is this moment at which we begin to realize the necessity of using numbers to represent our inputs and outputs. Individual terminologies such as "dough", "cookie dough", and the like, are not so easy to deal with because there is no fixed criterion under which they can be compared with each other in a consistent manner. The best we can do in such a circumstance is to merely list all possible scenarios.
Once we assign numerical values to the terms and line them up as a sequence, things start to become much more handy. Since they are quantities instead of just a bunch of qualitative indicators, we can now fully illustrate their input-output relations based upon a simple quantitative rule.
For example, suppose that different types of dough are denoted by single-digit numbers such as 0, 1, and 2, and that their baked results are denoted by double-digit numbers such as 10, 11, and 12, like the ones shown below.
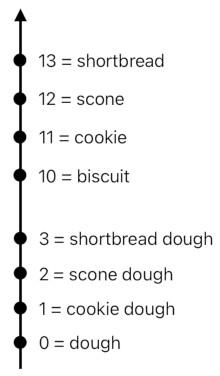
We are assuming here that both the inputs and outputs of the "bake" function are numerical values. The benefit of doing this is that now we are able to use an algebraic pattern to describe what the function does.
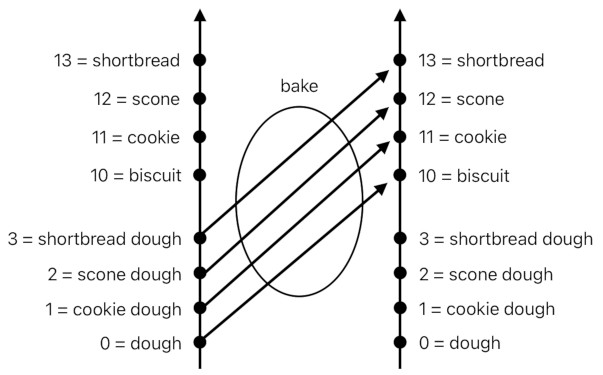
We know that baking a piece of dough gives us a biscuit, baking a piece of cookie dough gives us a cookie, baking a piece of scone dough gives us a scone, and baking a piece of shortbread dough gives us a shortbread. According to the given set of equivalences, it is also perfectly valid to say that baking 0 gives us 10, baking 1 gives us 11, baking 2 gives us 12, and baking 3 gives us 13. Do you see the pattern here? It means that baking something is the same as increasing its value by 10.

Now we have it. "output = input + 10" is the only formula we need to be able to derive the output of the "bake" function from any given input. This is the power of representing things numerically; since quantitative operators such as addition (+), subtraction (-), multiplication (x), and division (/) are endowed with the ability to easily summarize the way in which one set of things can be mapped into with another set of things.
One major concern which may arise here, though, is that utilizing numbers in the context of baking is perhaps a bit too "hacky". As you may have noticed already, attaching arbitrary numbers to a bunch of seemingly unrelated objects such as "dough", "cookie", "shortbread", and so on, feels way too random when we think about it. Why should "cookie" always be identified by number 11? Why can't it be 42, 990, -83794, or 51.230774 instead?
This is probably one of the main reasons why so many people hate mathematics. Numbers, when their roles are not explained thoroughly enough, present themselves as nothing more than a library of obscure symbols. And what is unfortunate is that the origin of such evil can be attributed to hardcore mathematicians who are obsessed with brevity; their love for ultra-minimalism encourages them to oversimplify everything, including the very reason why we decided to use numbers in the first place (I mean, yes, mathematicians do indeed explain why they are using certain variables, symbols, and so forth, but such explanations are mostly concealed inside their bush of technical eloquence).
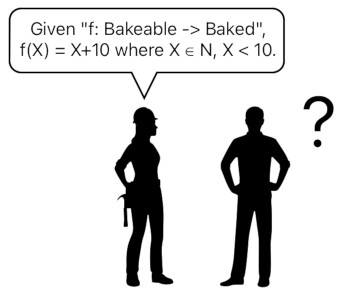
What we need is a down-to-earth illustration of what is going on, as well as why we need numbers for it. Once we are settled on that, we can then proceed to set up an agreeable standard as to the meaning of those numbers.
The biggest challenge is to establish an intuitively satisfying correlation between our practical interests and the way in which they are being represented. When we bake something, what we want to know is the type of the thing that we are baking, as well as the type of the thing that will result once baking is over. It is because we do not want to be ignorant of what we are putting into the oven and what we are getting out of it. We have an inherent desire to identify things we care, by means of names, numbers, or other identifiers.
And it is the heart of mathematical reasoning which guides us to the belief that numbers are the most preferred ones among such identifiers, due to the fact that their pre-established set of relations allow them to be mutually comparable. We cannot directly compare a biscuit with a cookie, but we can definitely compare the sweetness of a biscuit with the sweetness of a cookie because "sweetness" is something which can be characterized by a number (e.g. A small number refers to low sweetness, a large number refers to high sweetness, etc).
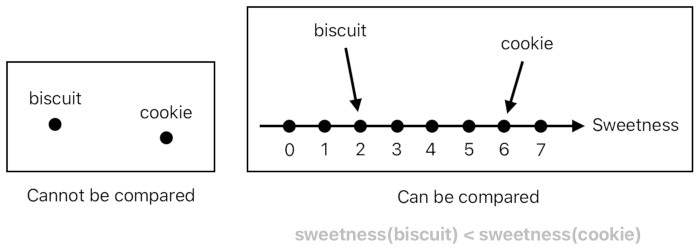
But then, of course, comparing sweetness is not the only option we have. We are also able to compare the size, weight, or color of the two desserts by means of numerical quantifiers. And it is necessary to realize that the same exact number (such as "3") can either mean sweetness, size, or weight, depending on what it is aiming to convey.
The problem is that it is not so easy to represent everything with just a single line of numbers. We need a multitude of them, each of which represents a separate dimension.
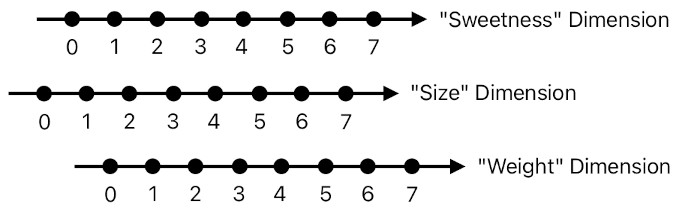
A dimension is a group of similar things which can be lined up as a sequence. The sweetness of a biscuit and the sweetness of a cookie are "similar" in the sense that they both belong to the same property called "sweetness", as well as that one of them either comes before or after the other in the spectrum of sweetness depending on what their values are. Therefore, they both belong to the same dimension which can be named "sweetness".
So now we have it. We are free to come up with any arbitrary dimensions, each of which corresponds to a category of things that are numerically comparable with one another.
We have an intuitive understanding that the "bake" function accepts a bakeable item as the input and returns a baked item as the output. What should be noted here is that there is a clear distinction between things that are eligible to be the input and things that are eligible to be the output; only those which are considered "bakeable" can possibly be the input of the function, and only those which are considered "baked" can possibly be the output of the function.
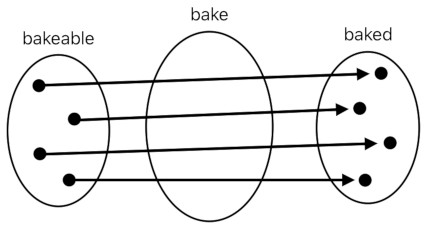
But again, we do not want to undertake the pain of having to specify every possible way in which a member of one group can be associated with a member of the other group. This can be avoided by introducing dimensions.
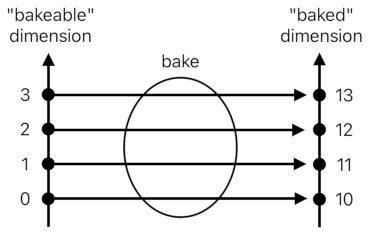
Here we have a dimension of bakeable objects, as well as a dimension of baked objects. Numbers in the bakeable-dimension are things which can be baked, and numbers in the baked-dimension are things which are the results of being baked.
Unfortunately, we are once again confronting the issue of semantics here. One can technically illustrate the aforementioned dimensions by saying, "10 is for biscuit! 11 is for cookie! 12 is for scone!" and so on, but such statements feel like they are out of nowhere. Hence, what does it imply when we compare one thing with another in this context? For example, if 11 denotes a cookie and 10 denotes a biscuit, does the fact that a cookie is 1 greater than a biscuit mean anything?
There would have not been such a problem of ambiguity if the dimensions referred to measurable quantities. So, let's rethink the nature of the "bake" function in terms of what can be measured.
Whenever we bake something, we are increasing the temperature of whatever is in the oven. So it seems that the input and output of the "bake" function could represent the initial and final temperatures of the oven's content, respectively. We can imagine that these two numbers both belong to the same dimension called "temperature".
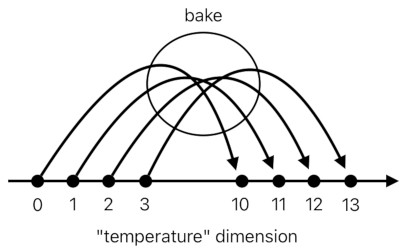
This looks fair enough, yet we know that such a formulation does not render the full picture of what is really happening. The art of baking is not just about changing the temperature of the dough! There are so many other physicochemical processes going on inside the oven, besides the addition of thermal energy. It will be insincere for us to blatantly ignore these intricate details just for the sake of simplicity.
(Will be continued in Part 3)
Previous Page Next Page
© 2019-2026 ThingsPool. All rights reserved.
Privacy Policy Terms of Service